注記
完全なコード例をダウンロードするには、最後まで移動してください。または、Binder経由でブラウザでこの例を実行するには
ヒト細胞(有糸分裂中)のセグメンテーション#
この例では、ヒト細胞の顕微鏡画像を分析します。Jason Moffat氏[1]がCellProfilerを通じて提供するデータを使用します。
import matplotlib.pyplot as plt
import numpy as np
from scipy import ndimage as ndi
import skimage as ski
image = ski.data.human_mitosis()
fig, ax = plt.subplots()
ax.imshow(image, cmap='gray')
ax.set_title('Microscopy image of human cells stained for nuclear DNA')
plt.show()

暗い背景に多くの細胞核が見えます。それらのほとんどは滑らかで楕円形をしています。しかし、有糸分裂(細胞分裂)中の核に対応する、より明るいスポットをいくつか見分けることができます。
グレースケール画像を可視化する別の方法は、等高線プロットです。
fig, ax = plt.subplots(figsize=(5, 5))
qcs = ax.contour(image, origin='image')
ax.set_title('Contour plot of the same raw image')
plt.show()
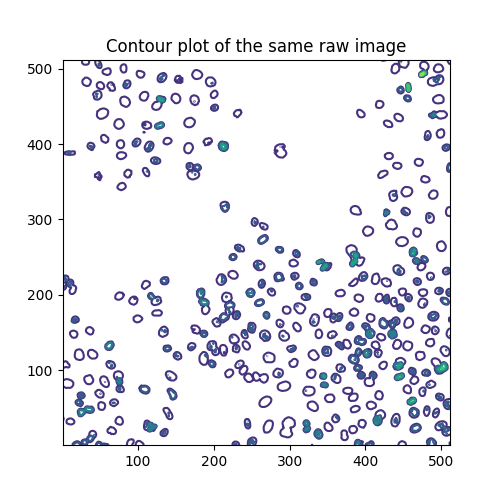
等高線はこれらのレベルで描画されます。
array([ 0., 40., 80., 120., 160., 200., 240., 280.])
各レベルには、それぞれ以下の数のセグメントがあります。
# Levels without segments still contain one empty array, account for that
[len(seg) if seg[0].size else 0 for seg in qcs.allsegs]
[0, 320, 270, 48, 19, 3, 1, 0]
有糸分裂指数の推定#
細胞生物学では、細胞分裂、ひいては細胞増殖を定量化するために有糸分裂指数を使用します。定義上、これは有糸分裂中の細胞数の全細胞数に対する比率です。上記の画像を分析するために、2つのしきい値に興味があります。1つは核を背景から分離するもの、もう1つは分裂中の核(明るいスポット)を分裂していない核から分離するものです。これら3つの異なるクラスのピクセルを分離するために、マルチ大津しきい値処理に頼ります。
thresholds = ski.filters.threshold_multiotsu(image, classes=3)
regions = np.digitize(image, bins=thresholds)
fig, ax = plt.subplots(ncols=2, figsize=(10, 5))
ax[0].imshow(image)
ax[0].set_title('Original')
ax[0].set_axis_off()
ax[1].imshow(regions)
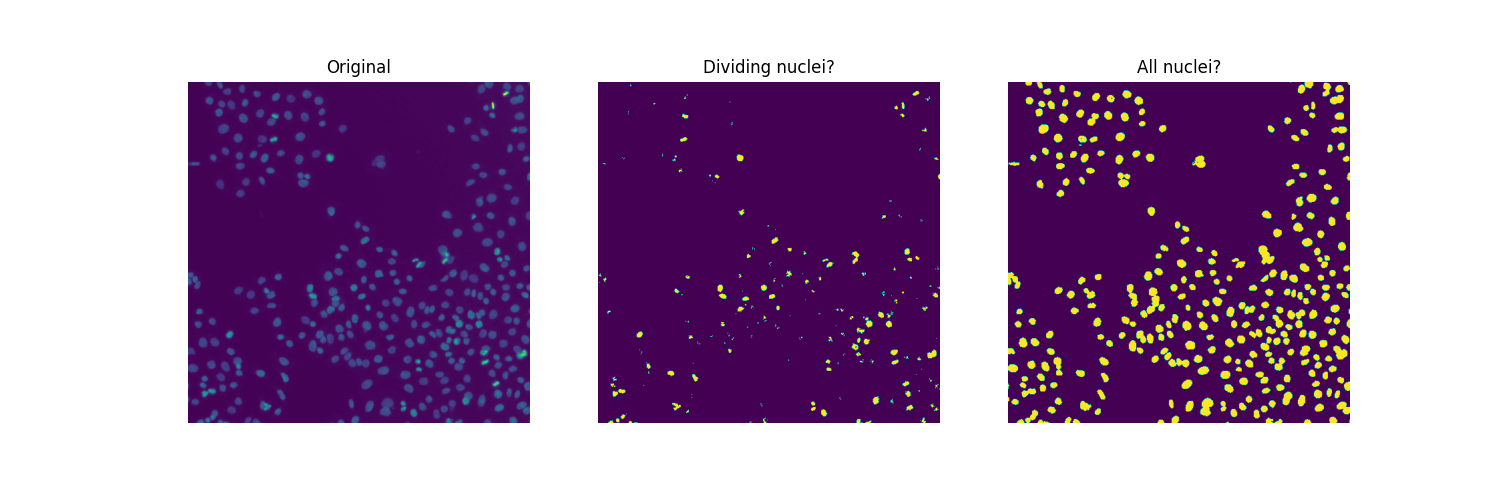
ax[1].set_title('Multi-Otsu thresholding')
ax[1].set_axis_off()
plt.show()

核が重複しているため、しきい値処理だけではすべての核をセグメント化するには不十分です。もしそうであれば、このサンプルの有糸分裂指数を簡単に計算できます。
cells = image > thresholds[0]
dividing = image > thresholds[1]
labeled_cells = ski.measure.label(cells)
labeled_dividing = ski.measure.label(dividing)
naive_mi = labeled_dividing.max() / labeled_cells.max()
print(naive_mi)
0.7847222222222222
これはありえません!分裂核の数
print(labeled_dividing.max())
226
は過大評価されており、細胞の総数
print(labeled_cells.max())
288
は過小評価されています。
分裂核のカウント#
明らかに、中央のプロットのすべての連結領域が分裂核であるわけではありません。一方で、2番目のしきい値(`thresholds[1]` の値)は、分裂核に対応する非常に明るい領域を、多くの核に存在する比較的明るいピクセルから分離するには低すぎるようです。他方で、小さな偽のオブジェクトを除去し、場合によっては隣接するオブジェクトのクラスタをマージする(いくつかは1つの細胞分裂から出現する2つの核に対応する可能性があります)、より滑らかな画像が必要です。ある意味で、分裂核で直面しているセグメンテーションの課題は、(接触している)細胞の課題とは反対です。
しきい値とフィルタリングパラメータに適切な値を見つけるために、視覚的および手動で二分法を進めます。
higher_threshold = 125
dividing = image > higher_threshold
smoother_dividing = ski.filters.rank.mean(
ski.util.img_as_ubyte(dividing), ski.morphology.disk(4)
)
binary_smoother_dividing = smoother_dividing > 20
fig, ax = plt.subplots(figsize=(5, 5))
ax.imshow(binary_smoother_dividing)
ax.set_title('Dividing nuclei')
ax.set_axis_off()
plt.show()
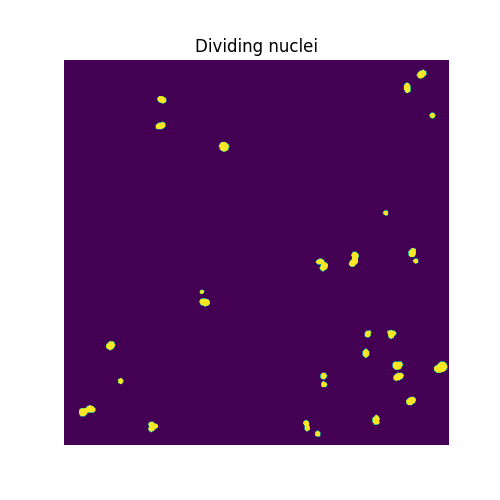
残っているのは
cleaned_dividing = ski.measure.label(binary_smoother_dividing)
print(cleaned_dividing.max())
29
このサンプル中の分裂核です。
核のセグメンテーション#
重複する核を分離するために、流域セグメンテーションに頼ります。アルゴリズムのアイデアは、一連の `markers` から氾濫した場合のように、流域を見つけることです。これらのマーカーは、背景までの距離関数の局所的最大値として生成します。核の典型的なサイズを考えると、局所的最大値、ひいてはマーカーが互いに少なくとも7ピクセル離れるように、`min_distance=7` を渡します。また、画像境界に接するすべての核が含まれるように、`exclude_border=False` も使用します。
distance = ndi.distance_transform_edt(cells)
local_max_coords = ski.feature.peak_local_max(
distance, min_distance=7, exclude_border=False
)
local_max_mask = np.zeros(distance.shape, dtype=bool)
local_max_mask[tuple(local_max_coords.T)] = True
markers = ski.measure.label(local_max_mask)
segmented_cells = ski.segmentation.watershed(-distance, markers, mask=cells)
セグメンテーションを便利に可視化するために、`color.label2rgb` 関数を使用してラベル付けされた領域を色分けし、引数 `bg_label=0` で背景ラベルを指定します。
fig, ax = plt.subplots(ncols=2, figsize=(10, 5))
ax[0].imshow(cells, cmap='gray')
ax[0].set_title('Overlapping nuclei')
ax[0].set_axis_off()
ax[1].imshow(ski.color.label2rgb(segmented_cells, bg_label=0))
ax[1].set_title('Segmented nuclei')
ax[1].set_axis_off()
plt.show()
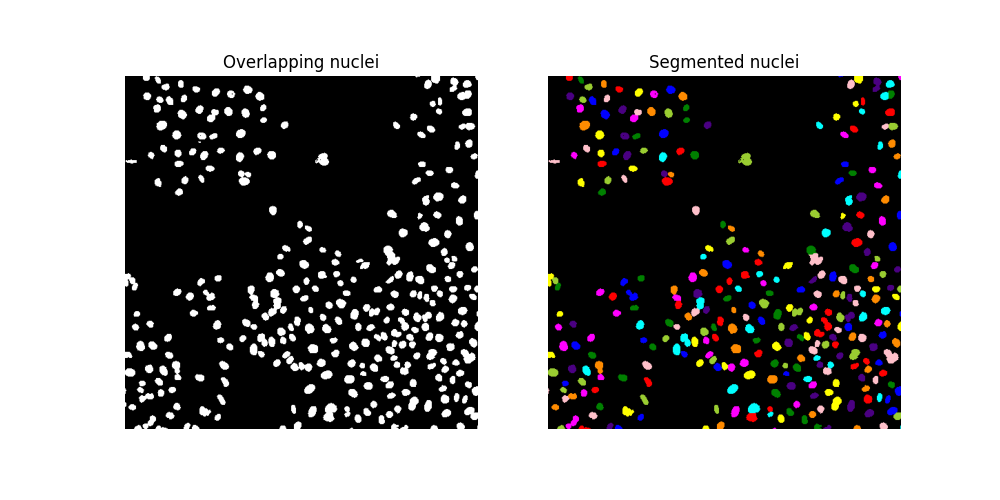
流域アルゴリズムによってより多くの核が識別されていることを確認してください。
assert segmented_cells.max() > labeled_cells.max()
最終的に、合計で
print(segmented_cells.max())
317
このサンプル中の細胞が見つかりました。したがって、有糸分裂指数は
print(cleaned_dividing.max() / segmented_cells.max())
0.0914826498422713
と推定されます。
