skimage.segmentation#
画像を意味のある領域または境界に分割するアルゴリズム。
アクティブ輪郭モデル。 |
|
チャン・ヴェーゼのセグメンテーションアルゴリズム。 |
|
バイナリ値を持つチェッカーボードのレベルセットを作成します。 |
|
ラベル画像の境界に接続されたオブジェクトをクリアします。 |
|
バイナリ値を持つディスクレベルセットを作成します。 |
|
重複することなく、ラベル画像内のラベルを |
|
フェルゼンツワルブの効率的なグラフベースの画像セグメンテーションを計算します。 |
|
ラベル付き領域間の境界が True であるブール配列を返します。 |
|
塗りつぶしに対応するマスク。 |
|
画像に対して塗りつぶしを実行します。 |
|
勾配の大きさの逆数。 |
|
2つの入力セグメンテーションの結合を返します。 |
|
ラベル付き領域間の境界が強調表示された画像を返します。 |
|
エッジのない形態学的アクティブ輪郭 (MorphACWE) |
|
形態学的測地的アクティブ輪郭 (MorphGAC)。 |
|
Color-(x,y) 空間でのクイックシフトクラスタリングを使用して画像をセグメント化します。 |
|
マーカーからのセグメンテーションのためのランダムウォーカーアルゴリズム。 |
|
任意のラベルを { |
|
Color-(x,y,z) 空間での k-means クラスタリングを使用して画像をセグメント化します。 |
|
指定されたマーカーからあふれた画像の分水界の流域を見つけます。 |
- skimage.segmentation.active_contour(image, snake, alpha=0.01, beta=0.1, w_line=0, w_edge=1, gamma=0.01, max_px_move=1.0, max_num_iter=2500, convergence=0.1, *, boundary_condition='periodic')[ソース]#
アクティブ輪郭モデル。
画像の特徴にスネークを適合させることによるアクティブ輪郭。単一およびマルチチャンネルの 2D 画像をサポートします。スネークは周期的(セグメンテーションの場合)または固定および/または自由端を持つことができます。出力スネークは、入力境界と同じ長さです。点の数は一定なので、最終的な輪郭の詳細をキャプチャするのに十分な点数が初期スネークにあることを確認してください。
- パラメーター:
- image(M, N) または (M, N, 3) ndarray
入力画像。
- snake(K, 2) ndarray
初期スネーク座標。周期的境界条件の場合、エンドポイントを複製しないでください。
- alphafloat, オプション
スネーク長の形状パラメータ。値が大きいほど、スネークはより速く収縮します。
- betafloat, オプション
スネークの滑らかさの形状パラメータ。値が大きいほど、スネークはより滑らかになります。
- w_linefloat, オプション
明るさへの引力を制御します。暗い領域に引き付けるには、負の値を使用してください。
- w_edgefloat, オプション
エッジへの引力を制御します。スネークをエッジから反発させるには、負の値を使用してください。
- gammafloat, オプション
明示的な時間ステップパラメータ。
- max_px_movefloat, オプション
反復ごとに移動する最大ピクセル距離。
- max_num_iterint, オプション
スネーク形状を最適化するための最大反復回数。
- convergencefloat, オプション
収束基準。
- boundary_conditionstring, オプション
輪郭の境界条件。'periodic'、'free'、'fixed'、'free-fixed'、または 'fixed-free' のいずれかになります。'periodic' はスネークの両端をアタッチし、'fixed' は端点を固定したままにし、'free' は端を自由に動かすことができます。'fixed' と 'free' は、'fixed-free'、'free-fixed' を解析することで組み合わせることができます。'fixed-fixed' または 'free-free' を解析すると、それぞれ 'fixed' および 'free' と同じ動作になります。
- 戻り値:
- snake(K, 2) ndarray
最適化されたスネーク。入力パラメータと同じ形状です。
参考文献
[1]Kass, M.; Witkin, A.; Terzopoulos, D. “Snakes: Active contour models”. International Journal of Computer Vision 1 (4): 321 (1988). DOI:10.1007/BF00133570
例
>>> from skimage.draw import circle_perimeter >>> from skimage.filters import gaussian
画像の作成と平滑化
>>> img = np.zeros((100, 100)) >>> rr, cc = circle_perimeter(35, 45, 25) >>> img[rr, cc] = 1 >>> img = gaussian(img, sigma=2, preserve_range=False)
スプラインを初期化
>>> s = np.linspace(0, 2*np.pi, 100) >>> init = 50 * np.array([np.sin(s), np.cos(s)]).T + 50
画像をスプラインに適合
>>> snake = active_contour(img, init, w_edge=0, w_line=1) >>> dist = np.sqrt((45-snake[:, 0])**2 + (35-snake[:, 1])**2) >>> int(np.mean(dist)) 25
- skimage.segmentation.chan_vese(image, mu=0.25, lambda1=1.0, lambda2=1.0, tol=0.001, max_num_iter=500, dt=0.5, init_level_set='checkerboard', extended_output=False)[ソース]#
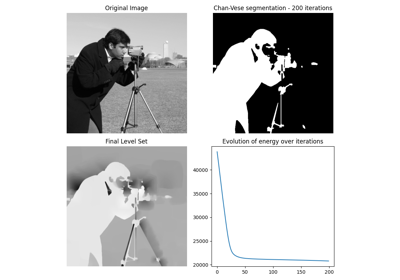
チャン・ヴェーゼのセグメンテーションアルゴリズム。
レベルセットを進化させることによるアクティブ輪郭モデル。明確に定義された境界のないオブジェクトをセグメント化するために使用できます。
- パラメーター:
- image(M, N) ndarray
セグメント化されるグレースケール画像。
- mufloat, オプション
「エッジ長」の重みパラメータ。値
muが大きいほど、「丸い」エッジが生成され、ゼロに近い値はより小さなオブジェクトを検出します。- lambda1float, オプション
値が「True」の出力領域の「平均からの差」の重みパラメータ。これが
lambda2より低い場合、この領域はもう一方の領域よりも値の範囲が広くなります。- lambda2float, オプション
値が「False」の出力領域の「平均からの差」の重みパラメータ。これが
lambda1より低い場合、この領域はもう一方の領域よりも値の範囲が広くなります。- tolfloat, 正, オプション
反復間のレベルセット変動許容値。連続反復のレベルセット間の L2 ノルム差が、画像の面積で正規化された後、この値を下回る場合、アルゴリズムはソリューションに到達したと想定します。
- max_num_iteruint, オプション
アルゴリズムが中断される前に許可される最大反復回数。
- dtfloat, オプション
各ステップの計算で適用される乗算係数。アルゴリズムを高速化するのに役立ちます。値が大きいほどアルゴリズムが高速化される可能性がありますが、収束の問題につながる可能性もあります。
- init_level_setstr または (M, N) ndarray, オプション
アルゴリズムで使用される開始レベルセットを定義します。文字列が入力された場合、画像サイズに一致するレベルセットが自動的に生成されます。または、カスタムレベルセットを定義することもできます。カスタムレベルセットは、「image」と同じ形状の浮動小数点値の配列である必要があります。受け入れられる文字列値は次のとおりです。
- 「チェッカーボード」
開始レベルセットは、sin(x/5*pi)*sin(y/5*pi) として定義されます。ここで、x と y はピクセル座標です。このレベルセットは収束が速いですが、暗黙的なエッジを検出できない場合があります。
- 「ディスク」
開始レベルセットは、画像の中心からの距離の逆数から画像幅と画像高さの最小値の半分を引いたものとして定義されます。これはやや遅いですが、暗黙的なエッジを適切に検出する可能性が高くなります。
- 「小さなディスク」
開始レベルセットは、画像の中心からの距離の逆数から、画像幅と画像高さの最小値の 4 分の 1 を引いたものとして定義されます。
- extended_outputbool, オプション
Trueに設定すると、戻り値は3つの戻り値を含むタプルになります(下記参照)。False(デフォルト値)に設定すると、'segmentation'配列のみが返されます。
- 戻り値:
- segmentation(M, N) ndarray, bool
アルゴリズムによって生成されたセグメンテーション。
- phi(M, N) ndarray of floats
アルゴリズムによって計算された最終的なレベルセット。
- energieslist of floats
アルゴリズムの各ステップにおける「エネルギー」の推移を示します。これにより、アルゴリズムが収束したかどうかを確認できます。
注
Chan-Veseアルゴリズムは、明確に定義された境界のないオブジェクトをセグメント化するように設計されています。このアルゴリズムは、レベルセットに基づいており、セグメント化された領域外の平均値からの強度差の合計、セグメント化された領域内の平均値からの差の合計、およびセグメント化された領域の境界の長さに依存する項に対応する重み付けされた値によって定義されるエネルギーを最小化するために反復的に進化します。
このアルゴリズムは、Tony ChanとLuminita Veseによって、"An Active Contour Model Without Edges" というタイトルの論文で最初に提案されました [1]。
このアルゴリズムの実装は、元の論文で説明されている面積係数 'nu' が実装されておらず、グレースケール画像にのみ適しているという意味で、やや簡略化されています。
lambda1とlambda2の典型的な値は1です。「背景」が分布の観点からセグメント化されたオブジェクトと大きく異なる場合(例えば、強度を変える図形がある一様な黒い画像)、これらの値は互いに異なる必要があります。muの典型的な値は0から1の間ですが、輪郭が非常に不明瞭な形状を扱う場合は、より高い値を使用できます。
このアルゴリズムが最小化しようとする「エネルギー」は、領域内の平均からの差の二乗の合計に、輪郭の長さと「mu」係数を掛けたものを加えたものとして定義されます。
2Dグレースケール画像のみをサポートしており、元の論文で説明されている面積項は実装されていません。
参考文献
[1]An Active Contour Model without Edges, Tony Chan and Luminita Vese, Scale-Space Theories in Computer Vision, 1999, DOI:10.1007/3-540-48236-9_13
[2]Chan-Vese Segmentation, Pascal Getreuer Image Processing On Line, 2 (2012), pp. 214-224, DOI:10.5201/ipol.2012.g-cv
[3]The Chan-Vese Algorithm - Project Report, Rami Cohen, 2011 arXiv:1107.2782
- skimage.segmentation.checkerboard_level_set(image_shape, square_size=5)[source]#
バイナリ値を持つチェッカーボードのレベルセットを作成します。
- パラメーター:
- image_shape正の整数のタプル
画像の形状。
- square_sizeint, optional
チェッカーボードの正方形のサイズ。デフォルトは5です。
- 戻り値:
- out形状が
image_shapeの配列 チェッカーボードの二値レベルセット。
- out形状が
- skimage.segmentation.clear_border(labels, buffer_size=0, bgval=0, mask=None, *, out=None)[source]#
ラベル画像の境界に接続されたオブジェクトをクリアします。
- パラメーター:
- labels(M[, N[, …, P]]) intまたはboolの配列
画像データのラベル。
- buffer_sizeint, optional
検査する境界の幅。デフォルトでは、画像の外部に接するオブジェクトのみが削除されます。
- bgvalfloatまたはint, optional
クリアされたオブジェクトはこの値に設定されます。
- mask
imageと同じ形状のboolのndarray, optional。 画像データマスク。マスクのFalseピクセルと重なるラベル画像のオブジェクトは削除されます。定義されている場合、引数buffer_sizeは無視されます。
- outndarray
labelsと同じ形状の配列で、出力が配置されます。デフォルトでは、新しい配列が作成されます。
- 戻り値:
- out(M[, N[, …, P]]) 配列
境界がクリアされた画像データラベル
例
>>> import numpy as np >>> from skimage.segmentation import clear_border >>> labels = np.array([[0, 0, 0, 0, 0, 0, 0, 1, 0], ... [1, 1, 0, 0, 1, 0, 0, 1, 0], ... [1, 1, 0, 1, 0, 1, 0, 0, 0], ... [0, 0, 0, 1, 1, 1, 1, 0, 0], ... [0, 1, 1, 1, 1, 1, 1, 1, 0], ... [0, 0, 0, 0, 0, 0, 0, 0, 0]]) >>> clear_border(labels) array([[0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 1, 0, 0, 0, 0], [0, 0, 0, 1, 0, 1, 0, 0, 0], [0, 0, 0, 1, 1, 1, 1, 0, 0], [0, 1, 1, 1, 1, 1, 1, 1, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0]]) >>> mask = np.array([[0, 0, 1, 1, 1, 1, 1, 1, 1], ... [0, 0, 1, 1, 1, 1, 1, 1, 1], ... [1, 1, 1, 1, 1, 1, 1, 1, 1], ... [1, 1, 1, 1, 1, 1, 1, 1, 1], ... [1, 1, 1, 1, 1, 1, 1, 1, 1], ... [1, 1, 1, 1, 1, 1, 1, 1, 1]]).astype(bool) >>> clear_border(labels, mask=mask) array([[0, 0, 0, 0, 0, 0, 0, 1, 0], [0, 0, 0, 0, 1, 0, 0, 1, 0], [0, 0, 0, 1, 0, 1, 0, 0, 0], [0, 0, 0, 1, 1, 1, 1, 0, 0], [0, 1, 1, 1, 1, 1, 1, 1, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0]])
- skimage.segmentation.disk_level_set(image_shape, *, center=None, radius=None)[source]#
バイナリ値を持つディスクレベルセットを作成します。
- パラメーター:
- image_shape正の整数のタプル
画像の形状
- center正の整数のタプル, optional
(行、列)で指定されたディスクの中心の座標。指定しない場合は、画像の中心がデフォルトになります。
- radiusfloat, optional
ディスクの半径。指定しない場合は、最小画像寸法の75%に設定されます。
- 戻り値:
- out形状が
image_shapeの配列 指定された
radiusとcenterを持つディスクの二値レベルセット。
- out形状が
- skimage.segmentation.expand_labels(label_image, distance=1, spacing=1)[source]#
重複することなく、ラベル画像内のラベルを
distanceピクセルで拡張します。ラベル画像が与えられた場合、
expand_labelsは、隣接する領域にオーバーフローすることなく、ラベル領域(連結成分)を最大distance単位まで外側に拡大します。具体的には、連結成分のdistanceピクセル以内のユークリッド距離内にある各背景ピクセルには、その連結成分のラベルが割り当てられます。spacingパラメータを使用すると、異方性画像のユークリッド距離を計算するために使用される距離変換の間隔を指定できます。複数の連結成分が背景ピクセルのdistanceピクセル内にある場合、最も近い連結成分のラベル値が割り当てられます(等距離に複数のラベルがある場合の注記を参照)。- パラメーター:
- label_imagedtype intのndarray
ラベル画像
- distancefloat
ラベルを拡大するピクセル単位のユークリッド距離。デフォルトは1です。
- spacingfloat、またはfloatのシーケンス, optional
各次元に沿った要素の間隔。シーケンスの場合、入力ランクと等しい長さでなければなりません。単一の数の場合、これはすべての軸に使用されます。指定しない場合、単位グリッド間隔が暗黙的に指定されます。
- 戻り値:
- enlarged_labelsdtype intのndarray
すべての連結領域が拡大されたラベル付き配列
注
ラベルが
distanceピクセル以上離れている場合、これは半径distanceのディスクまたは超球による形態学的拡張と同等です。ただし、形態学的拡張とは対照的に、expand_labelsはラベル領域を隣接する領域に拡張しません。この
expand_labelsの実装は、CellProfiler [1]に由来しており、モジュール「IdentifySecondaryObjects(Distance-N)」[2]として知られています。ピクセルが複数の領域から同じ距離にある場合、どの領域がその空間に拡張されるかは定義されていないため、重要なエッジケースがあります。ここで、正確な動作は、
scipy.ndimage.distance_transform_edtの上流の実装に依存します。参考文献
例
>>> labels = np.array([0, 1, 0, 0, 0, 0, 2]) >>> expand_labels(labels, distance=1) array([1, 1, 1, 0, 0, 2, 2])
ラベルは互いに上書きされません
>>> expand_labels(labels, distance=3) array([1, 1, 1, 1, 2, 2, 2])
同点の場合、動作は未定義ですが、現在、辞書式順序で
(0,) * ndimに最も近いラベルに解決されます。>>> labels_tied = np.array([0, 1, 0, 2, 0]) >>> expand_labels(labels_tied, 1) array([1, 1, 1, 2, 2]) >>> labels2d = np.array( ... [[0, 1, 0, 0], ... [2, 0, 0, 0], ... [0, 3, 0, 0]] ... ) >>> expand_labels(labels2d, 1) array([[2, 1, 1, 0], [2, 2, 0, 0], [2, 3, 3, 0]]) >>> expand_labels(labels2d, 1, spacing=[1, 0.5]) array([[1, 1, 1, 1], [2, 2, 2, 0], [3, 3, 3, 3]])
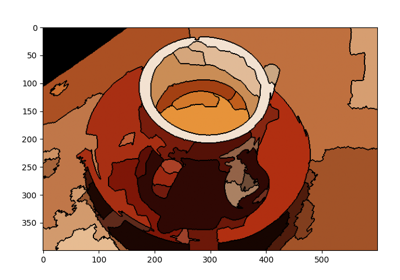
- skimage.segmentation.felzenszwalb(image, scale=1, sigma=0.8, min_size=20, *, channel_axis=-1)[source]#
Felsenszwalbの効率的なグラフベースの画像セグメンテーションを計算します。
画像グリッド上での高速な最小全域木ベースのクラスタリングを用いて、マルチチャネル(つまりRGB)画像の過剰セグメンテーションを生成します。パラメータ
scaleは観察レベルを設定します。スケールが大きいほど、セグメントは少なく、大きくなります。sigmaは、セグメンテーション前に画像を平滑化するために使用されるガウスカーネルの直径です。生成されるセグメントの数とそのサイズは、
scaleを通して間接的にのみ制御できます。画像内のセグメントのサイズは、ローカルコントラストに応じて大きく異なる可能性があります。RGB画像の場合、アルゴリズムは色空間におけるピクセル間のユークリッド距離を使用します。
- パラメーター:
- image(M, N[, 3]) ndarray
入力画像。
- scalefloat
自由パラメータ。大きいほど大きなクラスタになります。
- sigmafloat
前処理で使用されるガウスカーネルの幅(標準偏差)。
- min_sizeint
最小コンポーネントサイズ。後処理を使用して適用されます。
- channel_axisint または None, オプション
Noneの場合、画像はグレースケール(シングルチャネル)画像であると想定されます。それ以外の場合、このパラメータは、配列のどの軸がチャネルに対応するかを示します。
バージョン 0.19 で追加:
channel_axisは 0.19 で追加されました。
- 戻り値:
- segment_mask(M, N) ndarray
セグメントラベルを示す整数マスク。
注
元の論文で使用されていた
kパラメータは、ここではscaleに名前が変更されました。参考文献
[1]効率的なグラフベースの画像セグメンテーション, Felzenszwalb, P.F. and Huttenlocher, D.P. International Journal of Computer Vision, 2004
例
>>> from skimage.segmentation import felzenszwalb >>> from skimage.data import coffee >>> img = coffee() >>> segments = felzenszwalb(img, scale=3.0, sigma=0.95, min_size=5)
- skimage.segmentation.find_boundaries(label_img, connectivity=1, mode='thick', background=0)[ソース]#
ラベル付き領域間の境界が True であるブール配列を返します。
- パラメーター:
- label_imgint または bool の配列
異なる領域が異なる整数またはブール値でラベル付けされている配列。
- connectivityint in {1, …,
label_img.ndim}, オプション 隣接ピクセルのいずれかが異なるラベルを持っている場合、ピクセルは境界ピクセルと見なされます。
connectivityは、どのピクセルが隣接ピクセルと見なされるかを制御します。接続性1(デフォルト)は、エッジ(2Dの場合)または面(3Dの場合)を共有するピクセルが隣接ピクセルと見なされることを意味します。label_img.ndimの接続性は、角を共有するピクセルが隣接ピクセルと見なされることを意味します。- modestring in {‘thick’, ‘inner’, ‘outer’, ‘subpixel’}
境界をマークする方法
thick: 同じラベルのピクセル(
connectivityで定義)で完全に囲まれていないピクセルはすべて境界としてマークされます。これにより、境界は2ピクセルの太さになります。inner: オブジェクトの内側のピクセルを輪郭線で示し、背景ピクセルはそのままにします。
outer: オブジェクト境界の周りの背景のピクセルを輪郭線で示します。2つのオブジェクトが接触している場合、それらの境界もマークされます。
subpixel: 元のピクセル間のピクセルが適切に境界としてマークされた、2倍の画像を返します。
- backgroundint, オプション
モード「inner」および「outer」では、背景ラベルの定義が必要です。これらの2つの説明については、
modeを参照してください。
- 戻り値:
- boundaries
label_imgと同じ形状の bool の配列 Trueが境界ピクセルを表す bool 画像。modeが 'subpixel' に等しい場合、すべてのiについて、boundaries.shape[i]は2 * label_img.shape[i] - 1に等しくなります(ピクセルは他のすべてのピクセルペアの間に挿入されます)。
- boundaries
例
>>> labels = np.array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 5, 5, 5, 0, 0], ... [0, 0, 1, 1, 1, 5, 5, 5, 0, 0], ... [0, 0, 1, 1, 1, 5, 5, 5, 0, 0], ... [0, 0, 1, 1, 1, 5, 5, 5, 0, 0], ... [0, 0, 0, 0, 0, 5, 5, 5, 0, 0], ... [0, 0, 0, 0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]], dtype=np.uint8) >>> find_boundaries(labels, mode='thick').astype(np.uint8) array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 1, 1, 0], [0, 1, 1, 1, 1, 1, 0, 1, 1, 0], [0, 1, 1, 0, 1, 1, 0, 1, 1, 0], [0, 1, 1, 1, 1, 1, 0, 1, 1, 0], [0, 0, 1, 1, 1, 1, 1, 1, 1, 0], [0, 0, 0, 0, 0, 1, 1, 1, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]], dtype=uint8) >>> find_boundaries(labels, mode='inner').astype(np.uint8) array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 0, 1, 0, 0], [0, 0, 1, 0, 1, 1, 0, 1, 0, 0], [0, 0, 1, 1, 1, 1, 0, 1, 0, 0], [0, 0, 0, 0, 0, 1, 1, 1, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]], dtype=uint8) >>> find_boundaries(labels, mode='outer').astype(np.uint8) array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 0, 0, 1, 0], [0, 1, 0, 0, 1, 1, 0, 0, 1, 0], [0, 1, 0, 0, 1, 1, 0, 0, 1, 0], [0, 1, 0, 0, 1, 1, 0, 0, 1, 0], [0, 0, 1, 1, 1, 1, 0, 0, 1, 0], [0, 0, 0, 0, 0, 1, 1, 1, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]], dtype=uint8) >>> labels_small = labels[::2, ::3] >>> labels_small array([[0, 0, 0, 0], [0, 0, 5, 0], [0, 1, 5, 0], [0, 0, 5, 0], [0, 0, 0, 0]], dtype=uint8) >>> find_boundaries(labels_small, mode='subpixel').astype(np.uint8) array([[0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 1, 1, 1, 0], [0, 0, 0, 1, 0, 1, 0], [0, 1, 1, 1, 0, 1, 0], [0, 1, 0, 1, 0, 1, 0], [0, 1, 1, 1, 0, 1, 0], [0, 0, 0, 1, 0, 1, 0], [0, 0, 0, 1, 1, 1, 0], [0, 0, 0, 0, 0, 0, 0]], dtype=uint8) >>> bool_image = np.array([[False, False, False, False, False], ... [False, False, False, False, False], ... [False, False, True, True, True], ... [False, False, True, True, True], ... [False, False, True, True, True]], ... dtype=bool) >>> find_boundaries(bool_image) array([[False, False, False, False, False], [False, False, True, True, True], [False, True, True, True, True], [False, True, True, False, False], [False, True, True, False, False]])
- skimage.segmentation.flood(image, seed_point, *, footprint=None, connectivity=None, tolerance=None)[ソース]#
塗りつぶしに対応するマスク。
特定の
seed_pointから開始して、シード値と等しいか、tolerance以内の接続された点が見つかります。- パラメーター:
- imagendarray
n次元配列。
- seed_pointtuple または int
フラッドフィルを開始する開始点として使用される
image内の点。画像が1Dの場合、この点は整数として指定できます。- footprintndarray, オプション
評価される各ピクセルの近傍を決定するために使用されるフットプリント(構造化要素)。1と0のみを含み、
imageと同じ数の次元を持っている必要があります。指定しない場合、すべての隣接ピクセルが近傍の一部と見なされます(完全に接続)。- connectivityint, オプション
評価される各ピクセルの近傍を決定するために使用される数値。中心からの二乗距離が
connectivity以下の隣接ピクセルは、隣接ピクセルと見なされます。footprintが None の場合は無視されます。- tolerancefloat または int, オプション
None(デフォルト)の場合、隣接する値は、
seed_pointにおけるimageの初期値と厳密に等しい必要があります。これが最速です。値が指定されている場合は、すべての点で比較が行われ、初期値のトレランス内にある場合は塗りつぶされます(両端を含む)。
- 戻り値:
- maskndarray
imageと同じ形状のブール配列が返され、シードポイントに接続され、シードポイントと等しい(またはトレランス内)領域の値がTrueになります。他のすべての値はFalseです。
注
この操作の概念的な類似は、多くのラスターグラフィックプログラムの「塗りつぶしバケツ」ツールです。この関数は、塗りつぶしを表すマスクのみを返します。
メモリ上の理由からマスクではなくインデックスが必要な場合、ユーザーは結果で
numpy.nonzeroを実行し、インデックスを保存して、このマスクを破棄できます。例
>>> from skimage.morphology import flood >>> image = np.zeros((4, 7), dtype=int) >>> image[1:3, 1:3] = 1 >>> image[3, 0] = 1 >>> image[1:3, 4:6] = 2 >>> image[3, 6] = 3 >>> image array([[0, 0, 0, 0, 0, 0, 0], [0, 1, 1, 0, 2, 2, 0], [0, 1, 1, 0, 2, 2, 0], [1, 0, 0, 0, 0, 0, 3]])
接続されたものを、完全な接続性(対角線を含む)で5で塗りつぶします
>>> mask = flood(image, (1, 1)) >>> image_flooded = image.copy() >>> image_flooded[mask] = 5 >>> image_flooded array([[0, 0, 0, 0, 0, 0, 0], [0, 5, 5, 0, 2, 2, 0], [0, 5, 5, 0, 2, 2, 0], [5, 0, 0, 0, 0, 0, 3]])
接続されたものを、対角線を除外(接続性1)して5で塗りつぶします
>>> mask = flood(image, (1, 1), connectivity=1) >>> image_flooded = image.copy() >>> image_flooded[mask] = 5 >>> image_flooded array([[0, 0, 0, 0, 0, 0, 0], [0, 5, 5, 0, 2, 2, 0], [0, 5, 5, 0, 2, 2, 0], [1, 0, 0, 0, 0, 0, 3]])
許容範囲内で塗りつぶします
>>> mask = flood(image, (0, 0), tolerance=1) >>> image_flooded = image.copy() >>> image_flooded[mask] = 5 >>> image_flooded array([[5, 5, 5, 5, 5, 5, 5], [5, 5, 5, 5, 2, 2, 5], [5, 5, 5, 5, 2, 2, 5], [5, 5, 5, 5, 5, 5, 3]])
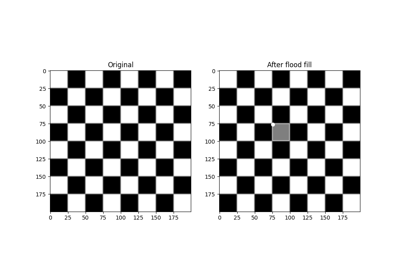
- skimage.segmentation.flood_fill(image, seed_point, new_value, *, footprint=None, connectivity=None, tolerance=None, in_place=False)[ソース]#
画像に対して塗りつぶしを実行します。
特定の
seed_pointから開始して、シード値と等しいか、tolerance以内の接続された点が見つかり、new_valueに設定されます。- パラメーター:
- imagendarray
n次元配列。
- seed_pointtuple または int
フラッドフィルを開始する開始点として使用される
image内の点。画像が1Dの場合、この点は整数として指定できます。- new_value
image型 塗りつぶし全体に設定する新しい値。これは、
imageの dtype と一致するように選択する必要があります。- footprintndarray, オプション
評価される各ピクセルの近傍を決定するために使用されるフットプリント(構造化要素)。1と0のみを含み、
imageと同じ数の次元を持っている必要があります。指定しない場合、すべての隣接ピクセルが近傍の一部と見なされます(完全に接続)。- connectivityint, オプション
評価される各ピクセルの近傍を決定するために使用される数値。中心からの二乗距離が
connectivity以下の隣接ピクセルは、隣接ピクセルと見なされます。footprintが None の場合は無視されます。- tolerancefloat または int, オプション
None(デフォルト)の場合、塗りつぶされるためには、隣接する値は
seed_pointにおけるimageの値と厳密に等しい必要があります。これが最速です。許容範囲が指定されている場合、シードポイントからプラスまたはマイナスの許容範囲内の値を持つ隣接ポイントが塗りつぶされます(両端を含む)。- in_placebool, オプション
Trueの場合、
imageに対してインプレースで塗りつぶしが行われます。Falseの場合、入力のimageを変更せずに、塗りつぶし結果が返されます(デフォルト)。
- 戻り値:
- filledndarray
imageと同じ形状の配列が返され、シード点に接続され、かつシード点と同じ値(または許容範囲内)を持つ領域の値がnew_valueに置き換えられます。
注
この操作の概念的なアナロジーは、多くのラスターグラフィックスプログラムの「塗りつぶし」ツールです。
例
>>> from skimage.morphology import flood_fill >>> image = np.zeros((4, 7), dtype=int) >>> image[1:3, 1:3] = 1 >>> image[3, 0] = 1 >>> image[1:3, 4:6] = 2 >>> image[3, 6] = 3 >>> image array([[0, 0, 0, 0, 0, 0, 0], [0, 1, 1, 0, 2, 2, 0], [0, 1, 1, 0, 2, 2, 0], [1, 0, 0, 0, 0, 0, 3]])
接続されたものを、完全な接続性(対角線を含む)で5で塗りつぶします
>>> flood_fill(image, (1, 1), 5) array([[0, 0, 0, 0, 0, 0, 0], [0, 5, 5, 0, 2, 2, 0], [0, 5, 5, 0, 2, 2, 0], [5, 0, 0, 0, 0, 0, 3]])
接続されたものを、対角線を除外(接続性1)して5で塗りつぶします
>>> flood_fill(image, (1, 1), 5, connectivity=1) array([[0, 0, 0, 0, 0, 0, 0], [0, 5, 5, 0, 2, 2, 0], [0, 5, 5, 0, 2, 2, 0], [1, 0, 0, 0, 0, 0, 3]])
許容範囲内で塗りつぶします
>>> flood_fill(image, (0, 0), 5, tolerance=1) array([[5, 5, 5, 5, 5, 5, 5], [5, 5, 5, 5, 2, 2, 5], [5, 5, 5, 5, 2, 2, 5], [5, 5, 5, 5, 5, 5, 3]])
- skimage.segmentation.inverse_gaussian_gradient(image, alpha=100.0, sigma=5.0)[ソース]#
勾配の大きさの逆数。
画像内の勾配の大きさを計算し、その結果を [0, 1] の範囲で反転します。平坦な領域には 1 に近い値が割り当てられ、境界に近い領域には 0 に近い値が割り当てられます。
この関数またはユーザーが定義した同様の関数は、
morphological_geodesic_active_contourを呼び出す前の前処理ステップとして画像に適用する必要があります。- パラメーター:
- image(M, N) または (L, M, N) 配列
グレースケール画像またはボリューム。
- alphafloat, オプション
反転の傾斜を制御します。値が大きいほど、結果の配列で平坦な領域と境界領域間の遷移が急峻になります。
- sigmafloat, optional
画像に適用されるガウシアンフィルターの標準偏差。
- 戻り値:
- gimage(M, N) または (L, M, N) 配列
morphological_geodesic_active_contourに適した前処理済み画像(またはボリューム)。
- skimage.segmentation.join_segmentations(s1, s2, return_mapping: bool = False)[ソース]#
2つの入力セグメンテーションの結合を返します。
S1 と S2 の結合 J は、2 つのボクセルが *両方* の S1 と S2 で同じセグメントにある場合にのみ、同じセグメントにあるセグメンテーションとして定義されます。
- パラメーター:
- s1, s2numpy 配列
s1 と s2 は同じ形状のラベルフィールドです。
- return_mappingbool, optional
True の場合、結合されたセグメンテーションラベルから元のラベルへのマッピングを返します。
- 戻り値:
- jnumpy 配列
s1 と s2 の結合セグメンテーション。
- map_j_to_s1ArrayMap, optional
結合されたセグメンテーション j のラベルから s1 のラベルへのマッピング。
- map_j_to_s2ArrayMap, optional
結合されたセグメンテーション j のラベルから s2 のラベルへのマッピング。
例
>>> from skimage.segmentation import join_segmentations >>> s1 = np.array([[0, 0, 1, 1], ... [0, 2, 1, 1], ... [2, 2, 2, 1]]) >>> s2 = np.array([[0, 1, 1, 0], ... [0, 1, 1, 0], ... [0, 1, 1, 1]]) >>> join_segmentations(s1, s2) array([[0, 1, 3, 2], [0, 5, 3, 2], [4, 5, 5, 3]]) >>> j, m1, m2 = join_segmentations(s1, s2, return_mapping=True) >>> m1 ArrayMap(array([0, 1, 2, 3, 4, 5]), array([0, 0, 1, 1, 2, 2])) >>> np.all(m1[j] == s1) True >>> np.all(m2[j] == s2) True
- skimage.segmentation.mark_boundaries(image, label_img, color=(1, 1, 0), outline_color=None, mode='outer', background_label=0)[ソース]#
ラベル付き領域間の境界が強調表示された画像を返します。
- パラメーター:
- image(M, N[, 3]) 配列
グレースケールまたは RGB 画像。
- label_img(M, N) 整数配列
領域が異なる整数値でマークされているラベル配列。
- color長さ 3 のシーケンス, optional
出力画像内の境界線の RGB カラー。
- outline_color長さ 3 のシーケンス, optional
出力画像内の境界線を囲む RGB カラー。None の場合、アウトラインは描画されません。
- mode{‘thick’, ‘inner’, ‘outer’, ‘subpixel’} の文字列, optional
境界線を検出するためのモード。
- background_labelint, optional
背景と見なすラベル(これは
innerおよびouterモードでのみ役立ちます)。
- 戻り値:
- marked(M, N, 3) float 配列
ラベル間の境界線が元の画像に重ねられた画像。
- skimage.segmentation.morphological_chan_vese(image, num_iter, init_level_set='checkerboard', smoothing=1, lambda1=1, lambda2=1, iter_callback=<function <lambda>>)[ソース]#
エッジのない形態学的アクティブ輪郭 (MorphACWE)
モルフォロジー演算子で実装された、エッジのないアクティブ輪郭。境界が明確に定義されていない画像およびボリューム内のオブジェクトをセグメント化するために使用できます。オブジェクトの内部が平均して外部と異なって見えることが必要です(つまり、オブジェクトの内部領域は、平均して外部領域よりも暗いか明るい必要があります)。
- パラメーター:
- image(M, N) または (L, M, N) 配列
セグメント化するグレースケール画像またはボリューム。
- num_iteruint
実行する num_iter の回数
- init_level_setstr, (M, N) 配列, または (L, M, N) 配列
初期レベルセット。配列が与えられた場合、バイナリ化され、初期レベルセットとして使用されます。文字列が与えられた場合、
imageの形状で妥当な初期レベルセットを生成する方法を定義します。受け入れられる値は「checkerboard」と「disk」です。これらのレベルセットがどのように作成されるかについての詳細は、checkerboard_level_setおよびdisk_level_setのドキュメントを参照してください。- smoothinguint, optional
反復ごとに平滑化演算子が適用される回数。妥当な値は 1〜4 程度です。値が大きいほど、セグメンテーションは滑らかになります。
- lambda1float, オプション
外部領域の重みパラメータ。
lambda1がlambda2よりも大きい場合、外部領域には内部領域よりも広い範囲の値が含まれます。- lambda2float, オプション
内部領域の重みパラメータ。
lambda2がlambda1よりも大きい場合、内部領域には外部領域よりも広い範囲の値が含まれます。- iter_callbackfunction, optional
指定された場合、この関数は反復ごとに一度、現在のレベルセットを唯一の引数として呼び出されます。これは、デバッグや進化中の途中結果のプロットに役立ちます。
- 戻り値:
- out(M, N) または (L, M, N) 配列
最終セグメンテーション(つまり、最終レベルセット)
注
これは、輪郭の進化のために偏微分方程式(PDE)を解く代わりに、モルフォロジー演算子を使用する Chan-Vese アルゴリズムのバージョンです。このアルゴリズムで使用されるモルフォロジー演算子のセットは、Chan-Vese PDE に無限小的に等価であることが証明されています([1]を参照)。ただし、モルフォロジー演算子は、PDE で一般的に見られる数値安定性の問題(進化のために適切なタイムステップを見つける必要がない)に悩まされることがなく、計算が高速です。
アルゴリズムとその理論的導出は [1] に記載されています。
参考文献
[1] (1,2)曲線と曲面の曲率に基づく進化のための形態学的アプローチ、パブロ・マルケス-ネイラ、ルイス・バウメラ、ルイス・アルバレス。IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), 2014, DOI:10.1109/TPAMI.2013.106
- skimage.segmentation.morphological_geodesic_active_contour(gimage, num_iter, init_level_set='disk', smoothing=1, threshold='auto', balloon=0, iter_callback=<function <lambda>>)[source]#
形態学的測地的アクティブ輪郭 (MorphGAC)。
モルフォロジー演算子で実装された測地線アクティブ輪郭。可視ではあるがノイズが多く、乱雑で、途切れた境界を持つオブジェクトをセグメント化するために使用できます。
- パラメーター:
- gimage(M, N) または (L, M, N) 配列
セグメント化される前処理された画像またはボリューム。これは元の画像であることは非常にまれです。代わりに、これは通常、セグメント化するオブジェクトの境界(またはその他の構造)を強調および強調する元の画像の前処理されたバージョンです。
morphological_geodesic_active_contour()は、gimageが小さい領域での輪郭の進化を停止しようとします。この前処理を実行する関数の例として、inverse_gaussian_gradient()を参照してください。morphological_geodesic_active_contour()の品質は、この前処理に大きく依存する可能性があることに注意してください。- num_iteruint
実行する num_iter の数。
- init_level_setstr, (M, N) 配列, または (L, M, N) 配列
初期レベルセット。配列が与えられた場合、バイナリ化され、初期レベルセットとして使用されます。文字列が与えられた場合、
imageの形状で妥当な初期レベルセットを生成する方法を定義します。受け入れられる値は「checkerboard」と「disk」です。これらのレベルセットがどのように作成されるかについての詳細は、checkerboard_level_setおよびdisk_level_setのドキュメントを参照してください。- smoothinguint, optional
反復ごとに平滑化演算子が適用される回数。妥当な値は 1〜4 程度です。値が大きいほど、セグメンテーションは滑らかになります。
- thresholdfloat, オプション
この閾値よりも小さい値を持つ画像の領域は、境界と見なされます。輪郭の進化はこれらの領域で停止します。
- balloonfloat, オプション
画像の非情報領域、つまり画像の勾配が小さすぎて輪郭を境界に向かって押し出すことができない領域で、輪郭を誘導するバルーン力。負の値は輪郭を縮小し、正の値はこれらの領域で輪郭を拡大します。これをゼロに設定すると、バルーン力が無効になります。
- iter_callbackfunction, optional
指定された場合、この関数は反復ごとに一度、現在のレベルセットを唯一の引数として呼び出されます。これは、デバッグや進化中の途中結果のプロットに役立ちます。
- 戻り値:
- out(M, N) または (L, M, N) 配列
最終セグメンテーション(つまり、最終レベルセット)
注
これは、輪郭の進化のために偏微分方程式(PDE)を解くのではなく、モルフォロジー演算子を使用する測地線アクティブ輪郭(GAC)アルゴリズムのバージョンです。このアルゴリズムで使用されるモルフォロジー演算子のセットは、GAC PDEと無限小で同等であることが証明されています([1]を参照)。ただし、モルフォロジー演算子は、PDEで一般的に見られる数値安定性の問題(たとえば、進化に適したタイムステップを見つける必要がない)の影響を受けず、計算が高速です。
アルゴリズムとその理論的導出は[1]に記載されています。
参考文献
[1] (1,2)曲線と曲面の曲率に基づく進化のための形態学的アプローチ、パブロ・マルケス-ネイラ、ルイス・バウメラ、ルイス・アルバレス。IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), 2014, DOI:10.1109/TPAMI.2013.106
- skimage.segmentation.quickshift(image, ratio=1.0, kernel_size=5, max_dist=10, return_tree=False, sigma=0, convert2lab=True, rng=42, *, channel_axis=-1)[source]#
Color-(x,y) 空間でのクイックシフトクラスタリングを使用して画像をセグメント化します。
クイックシフト モード検索アルゴリズムを使用して、画像の過剰セグメンテーションを生成します。
- パラメーター:
- image(M, N, C) ndarray
入力画像。カラーチャネルに対応する軸は、
channel_axis引数で指定できます。- ratiofloat, オプション, 0~1の間
色空間の近接性と画像空間の近接性のバランスを取ります。値が大きいほど、色空間に重点が置かれます。
- kernel_sizefloat, オプション
サンプル密度を平滑化する際に使用されるガウス カーネルの幅。高いほどクラスターが少なくなります。
- max_distfloat, オプション
データ距離のカットオフ点。高いほどクラスターが少なくなります。
- return_treebool, オプション
セグメンテーション階層ツリーと距離を完全に戻すかどうか。
- sigmafloat, optional
前処理としてのガウス平滑化の幅。ゼロは平滑化しないことを意味します。
- convert2labbool, オプション
セグメンテーションの前に、入力をLabカラースペースに変換する必要があるかどうか。この目的のために、入力はRGBであると想定されます。
- rng{
numpy.random.Generator, int}, オプション 擬似乱数ジェネレーター。デフォルトでは、PCG64ジェネレーターが使用されます(
numpy.random.default_rng()を参照)。rngがintの場合、ジェネレーターのシードに使用されます。PRNGは、タイブレークに使用され、デフォルトで42でシードされます。
- channel_axisint, オプション
imageのカラーチャネルに対応する軸。デフォルトは最後の軸です。
- 戻り値:
- segment_mask(M, N) ndarray
セグメントラベルを示す整数マスク。
注
著者は、セグメンテーションの前に画像をLabカラースペースに変換することを推奨していますが、これは厳密には必須ではありません。これが機能するためには、画像をRGB形式で指定する必要があります。
参考文献
[1]モード探索のためのクイックシフトおよびカーネル法、ヴェダルディ、A.およびソアット、S. 欧州コンピュータビジョン会議、2008年
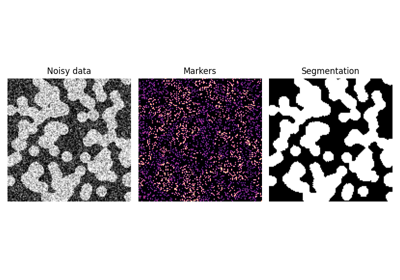
- skimage.segmentation.random_walker(data, labels, beta=130, mode='cg_j', tol=0.001, copy=True, return_full_prob=False, spacing=None, *, prob_tol=0.001, channel_axis=None)[source]#
マーカーからのセグメンテーションのためのランダムウォーカーアルゴリズム。
ランダムウォーカー アルゴリズムは、グレースケールまたはマルチチャネル画像用に実装されています。
- パラメーター:
- data(M, N[, P][, C]) ndarray
フェーズでセグメント化される画像。グレースケール
dataは、2次元または3次元にすることができます。マルチチャネルデータは、チャネルを含む次元を指定するchannel_axisを使用して、3次元または4次元にすることができます。spacingキーワード引数が使用されていない限り、データ間隔は等方性であると想定されます。- labels(M, N[, P]) intの配列
異なるフェーズに対して、異なる正の整数でラベル付けされたシードマーカーの配列。ゼロラベルのピクセルはラベル付けされていないピクセルです。負のラベルは、考慮されない非アクティブなピクセルに対応します(グラフから削除されます)。ラベルが連続した整数でない場合、ラベル配列は連続したラベルになるように変換されます。マルチチャネルの場合、
labelsは、dataの単一チャネルと同じ形状である必要があります。つまり、チャネルを示す最後の次元は含めません。- betafloat, オプション
ランダムウォーカー運動のペナルティ係数(
betaが大きいほど、拡散はより困難になります)。- mode文字列, 利用可能なオプション:{‘cg’, ‘cg_j’, ‘cg_mg’, ‘bf’}
ランダムウォーカーアルゴリズムで線形システムを解くためのモード。
‘bf’(総当たり):ラプラシアンのLU分解が計算されます。これは、小さな画像(1024x1024未満)では高速ですが、大きな画像(3Dボリュームなど)では非常に遅く、メモリを大量に消費します。
‘cg’(共役勾配法):線形システムは、scipy.sparse.linalgの共役勾配法を使用して反復的に解かれます。これは、大きな画像では総当たり法よりもメモリ消費量が少なくなりますが、非常に遅いです。
‘cg_j’(ヤコビ前処理付き共役勾配法):ヤコビ前処理が共役勾配法の反復中に適用されます。これにより、’cg’法の収束が加速される可能性があります。
‘cg_mg’(マルチグリッド前処理付き共役勾配法):マルチグリッドソルバーを使用して前処理が計算され、その後、共役勾配法で解が計算されます。このモードでは、pyamgモジュールがインストールされている必要があります。
- tolfloat, オプション
共役勾配ベースのモード(‘cg’、‘cg_j’、および ‘cg_mg’)を使用して線形システムを解くときに達成する許容誤差。
- copybool, オプション
copyがFalseの場合、
labels配列はセグメンテーションの結果で上書きされます。メモリを節約したい場合は、copy=Falseを使用してください。- return_full_probbool, オプション
Trueの場合、最も可能性の高いラベルのみではなく、ピクセルが各ラベルに属する確率が返されます。
- spacingfloatのイテラブル, オプション
各空間次元のボクセル間の間隔。
Noneの場合、各次元のピクセル/ボクセル間の間隔は1と見なされます。- prob_tolfloat, オプション
結果の確率が区間[0, 1]にあるための許容誤差。許容誤差が満たされない場合は、警告が表示されます。
- channel_axisint または None, オプション
Noneの場合、画像はグレースケール(シングルチャネル)画像であると想定されます。それ以外の場合、このパラメータは、配列のどの軸がチャネルに対応するかを示します。
バージョン 0.19 で追加:
channel_axisは 0.19 で追加されました。
- 戻り値:
- outputndarray
return_full_probがFalseの場合、labelsと同じ形状およびデータ型の整数の配列。各ピクセルは、異方性拡散によって最初にピクセルに到達したマーカーに従ってラベル付けされています。return_full_probがTrueの場合、形状(nlabels, labels.shape)の float の配列。output[label_nb, i, j]は、ラベルlabel_nbが最初にピクセル(i, j)に到達する確率です。
参照
skimage.segmentation.watershed数理形態学とマーカーからの領域の「フラッディング」に基づくセグメンテーションアルゴリズム。
注
マルチチャネル入力は、すべてのチャネルデータを組み合わせてスケーリングされます。このアルゴリズムを実行する前に、すべてのチャネルが個別に正規化されていることを確認してください。
spacing引数は、データ点が1つ以上の空間次元で異なる間隔で配置されている異方性データセットに固有です。異方性データは、医療画像でよく見られます。このアルゴリズムは、最初に[1]で提案されました。
このアルゴリズムは、各フェーズのマーカーに配置されたソースに対して、無限の時間における拡散方程式を解きます。ピクセルは、最初にピクセルに拡散する確率が最も高いフェーズでラベル付けされます。
拡散方程式は、各フェーズについて x.T L x を最小化することで解かれます。ここで、Lは画像の重み付きグラフのラプラシアンであり、xは、与えられたフェーズのマーカーが拡散によって最初にピクセルに到達する確率です(xは、フェーズのマーカーでは1、他のマーカーでは0になり、その他の係数が求められます)。各ピクセルには、xの最大値を持つラベルが割り当てられます。画像のラプラシアンLは、次のように定義されます。
L_ii = d_i、ピクセルiの近傍数(iの次数)
L_ij = iとjが隣接するピクセルの場合、-w_ij
重みw_ijは、局所勾配のノルムの減少関数です。これにより、類似の値のピクセル間で拡散が容易になります。
ラプラシアンがマークされたピクセルとマークされていないピクセルのブロックに分解される場合
L = M B.T B A
最初のインデックスはマークされたピクセルに対応し、その後マークされていないピクセルに対応し、1つのフェーズに対して x.T L x を最小化することは、次のことを解くことになります。
A x = - B x_m
ここで、x_mは、与えられたフェーズのマーカーで1、他のマーカーで0になります。この線形システムは、小さい画像には直接法を、大きい画像には反復法を使用してアルゴリズムで解かれます。
参考文献
[1]Leo Grady, Random walks for image segmentation, IEEE Trans Pattern Anal Mach Intell. 2006 Nov;28(11):1768-83. DOI:10.1109/TPAMI.2006.233.
例
>>> rng = np.random.default_rng() >>> a = np.zeros((10, 10)) + 0.2 * rng.random((10, 10)) >>> a[5:8, 5:8] += 1 >>> b = np.zeros_like(a, dtype=np.int32) >>> b[3, 3] = 1 # Marker for first phase >>> b[6, 6] = 2 # Marker for second phase >>> random_walker(a, b) array([[1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 2, 2, 2, 1, 1], [1, 1, 1, 1, 1, 2, 2, 2, 1, 1], [1, 1, 1, 1, 1, 2, 2, 2, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]], dtype=int32)
- skimage.segmentation.relabel_sequential(label_field, offset=1)[ソース]#
任意のラベルを {
offset, …offset+ ラベル数} にリラベルします。この関数は、前方マップ(元のラベルを縮小されたラベルにマッピング)と逆マップ(縮小されたラベルを元のラベルに戻すマッピング)も返します。
- パラメーター:
- label_fieldintのnumpy配列, 任意の形状
ラベルの配列。負でない整数である必要があります。
- offsetint, オプション
戻り値のラベルは
offsetから始まり、正である必要があります。
- 戻り値:
- relabeledintのnumpy配列,
label_fieldと同じ形状 ラベルが{offset, …, ラベル数 + offset - 1}にマッピングされた入力ラベルフィールド。データ型は、
label_fieldと同じになります。ただし、offset + ラベル数が現在のデータ型のオーバーフローを引き起こす場合は例外です。- forward_mapArrayMap
元のラベル空間から返されたラベル空間へのマップ。同じマッピングを再適用するために使用できます。使用例については、例を参照してください。出力データ型は、
relabeledと同じになります。- inverse_mapArrayMap
新しいラベル空間から元の空間へのマップ。これは、リラベルされたものから元のラベルフィールドを再構築するために使用できます。出力データ型は、
label_fieldと同じになります。
- relabeledintのnumpy配列,
注
ラベル0は背景を示すと想定されており、再マッピングされることはありません。
前方マップは、その長さがラベルフィールドの最大値で与えられるため、一部の入力では非常に大きくなる可能性があります。ただし、ほとんどの場合、
label_field.max()はlabel_field.sizeよりはるかに小さく、これらの場合、前方マップは入力画像または出力画像のいずれよりも小さくなることが保証されています。例
>>> from skimage.segmentation import relabel_sequential >>> label_field = np.array([1, 1, 5, 5, 8, 99, 42]) >>> relab, fw, inv = relabel_sequential(label_field) >>> relab array([1, 1, 2, 2, 3, 5, 4]) >>> print(fw) ArrayMap: 1 → 1 5 → 2 8 → 3 42 → 4 99 → 5 >>> np.array(fw) array([0, 1, 0, 0, 0, 2, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5]) >>> np.array(inv) array([ 0, 1, 5, 8, 42, 99]) >>> (fw[label_field] == relab).all() True >>> (inv[relab] == label_field).all() True >>> relab, fw, inv = relabel_sequential(label_field, offset=5) >>> relab array([5, 5, 6, 6, 7, 9, 8])
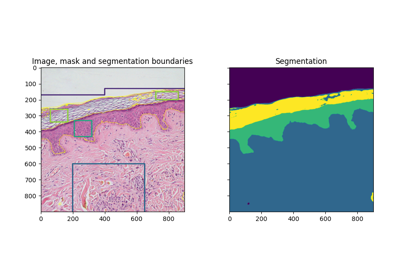
- skimage.segmentation.slic(image, n_segments=100, compactness=10.0, max_num_iter=10, sigma=0, spacing=None, convert2lab=None, enforce_connectivity=True, min_size_factor=0.5, max_size_factor=3, slic_zero=False, start_label=1, mask=None, *, channel_axis=-1)[ソース]#
Color-(x,y,z) 空間での k-means クラスタリングを使用して画像をセグメント化します。
- パラメーター:
- image(M, N[, P][, C]) ndarray
入力画像。2Dまたは3D、グレースケールまたはマルチチャネル(
channel_axisパラメータを参照)にすることができます。入力画像はNaNを含まないか、NaNがマスクされている必要があります。- n_segmentsint, オプション
セグメント化された出力画像におけるラベルの(おおよその)数。
- compactnessfloat, オプション
色の近さと空間的な近さのバランスを取ります。値が大きいほど空間的な近さが重視され、スーパーピクセルの形状がより正方形/立方体に近づきます。SLICOモードでは、これが初期のコンパクトさです。このパラメータは、画像のコントラストや画像内のオブジェクトの形状に大きく依存します。選択した値の周辺を調整する前に、0.01、0.1、1、10、100などの対数スケールで可能な値を検討することをお勧めします。
- max_num_iterint, オプション
k平均法の最大イテレーション数。
- sigmafloat または float の配列, オプション
画像の各次元に対する前処理のためのガウス平滑化カーネルの幅。スカラー値の場合、同じシグマが各次元に適用されます。ゼロは平滑化がないことを意味します。
sigmaがスカラーで、手動のボクセル間隔が指定されている場合(注釈セクションを参照)、自動的にスケーリングされることに注意してください。 sigma が配列のような場合、そのサイズはimageの空間次元の数と一致する必要があります。- spacingfloat の配列, オプション
各空間次元に沿ったボクセル間隔。デフォルトでは、
slicは均一な間隔(各空間次元に沿って同じボクセル解像度)を想定しています。このパラメータは、k平均法クラスタリング中の空間次元に沿った距離の重みを制御します。- convert2labbool, オプション
セグメンテーションの前に、入力をLabカラースペースに変換するかどうか。入力画像は必ずRGBである必要があります。強く推奨されます。このオプションは、
channel_axis` が None ではない *かつ* ``image.shape[-1] == 3の場合、デフォルトでTrueになります。- enforce_connectivitybool, オプション
生成されたセグメントが連結されているかどうか
- min_size_factorfloat, オプション
想定されるセグメントサイズ
`depth*width*height/n_segments`に対して削除される最小セグメントサイズの割合- max_size_factorfloat, オプション
最大連結セグメントサイズの割合。ほとんどの場合、3の値が機能します。
- slic_zerobool, オプション
SLIC-zero、SLICのゼロパラメータモードを実行します。[2]
- start_labelint, オプション
ラベルのインデックス開始。0または1である必要があります。
バージョン 0.17 で追加:
start_labelは 0.17 で導入されました- maskndarray, オプション
指定されている場合、スーパーピクセルはmaskがTrueの場合にのみ計算され、シードポイントはk平均法クラスタリング戦略を使用してマスク上に均質に分布します。マスクの次元数は、画像の空間次元の数と等しい必要があります。
バージョン 0.17 で追加:
maskは 0.17 で導入されました- channel_axisint または None, オプション
Noneの場合、画像はグレースケール(シングルチャネル)画像であると想定されます。それ以外の場合、このパラメータは、配列のどの軸がチャネルに対応するかを示します。
バージョン 0.19 で追加:
channel_axisは 0.19 で追加されました。
- 戻り値:
- labels2D または 3D 配列
セグメントラベルを示す整数マスク。
- Raises:
- ValueError
convert2labがTrueに設定されているが、配列の最後の次元の長さが3でない場合。- ValueError
start_labelが0または1でない場合。- ValueError
imageにマスクされていないNaN値が含まれている場合。- ValueError
imageにマスクされていない無限値が含まれている場合。- ValueError
imageが2Dだが、channel_axisが-1(デフォルト)の場合。
注
sigma > 0の場合、セグメンテーションの前にガウスカーネルを使用して画像が平滑化されます。sigmaがスカラーでspacingが指定されている場合、カーネル幅は各次元に沿って間隔で除算されます。たとえば、sigma=1でspacing=[5, 1, 1]の場合、有効なsigmaは[0.2, 1, 1]になります。これにより、異方性画像に対して適切な平滑化が保証されます。画像は、処理前に[0, 1]にリスケールされます(マスクされた値は無視されます)。
形状(M, N, 3)の画像は、デフォルトで2D RGB画像として解釈されます。最後の次元が長さ3である3Dとして解釈するには、
channel_axis=Noneを使用します。start_labelは、問題 [4] を処理するために導入されました。ラベルのインデックス付けは、デフォルトでは1から始まります。
参考文献
[1]Radhakrishna Achanta, Appu Shaji, Kevin Smith, Aurelien Lucchi, Pascal Fua, および Sabine Süsstrunk, SLIC Superpixels Compared to State-of-the-art Superpixel Methods, TPAMI, May 2012. DOI:10.1109/TPAMI.2012.120
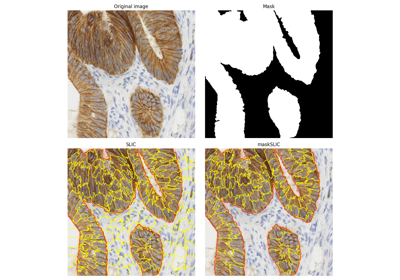
[3]Irving, Benjamin. “maskSLIC: regional superpixel generation with application to local pathology characterisation in medical images.”, 2016, arXiv:1606.09518
例
>>> from skimage.segmentation import slic >>> from skimage.data import astronaut >>> img = astronaut() >>> segments = slic(img, n_segments=100, compactness=10)
コンパクトさのパラメータを大きくすると、より正方形の領域が生成されます
>>> segments = slic(img, n_segments=100, compactness=20)
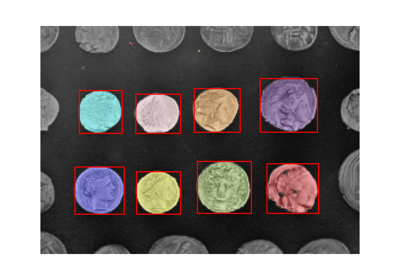
- skimage.segmentation.watershed(image, markers=None, connectivity=1, offset=None, mask=None, compactness=0, watershed_line=False)[source]#
指定されたマーカーからあふれた画像の分水界の流域を見つけます。
- パラメーター:
- image(M, N[, …]) ndarray
最も低い値のポイントが最初にラベル付けされるデータ配列。
- markersint, または int の (M, N[, …]) ndarray, オプション
目的の流域の数、またはラベルマトリックスに割り当てる値で流域をマークする配列。ゼロはマーカーではないことを意味します。Noneの場合、(デフォルトの)マーカーは、
imageの局所最小値として決定されます。具体的には、計算は、skimage.morphology.local_minima()をimageに適用し、続いてskimage.measure.label()を結果に適用することと同等です(同じ指定されたconnectivityを使用)。一般的に、ユーザーはマーカーを明示的に渡すことをお勧めします。- connectivityint または ndarray, オプション
近傍の連結性。整数は、
scipy.ndimage.generate_binary_structureで、隣接に到達するための直交ステップの最大数として解釈されます。配列は、フットプリント(構造要素)として直接解釈されます。デフォルト値は1です。2Dでは、1は4近傍を与え、2は8近傍を与えます。- offsetimage.ndim の形状の array_like, オプション
フットプリントの中心の座標。
- maskbool または 0 と 1 の (M, N[, …]) ndarray, オプション
imageと同じ形状の配列。mask == True であるポイントのみがラベル付けされます。- compactnessfloat, オプション
指定されたコンパクトさパラメータを持つコンパクトなウォーターシェッド [1] を使用します。値が大きいほど、より規則的な形状のウォーターシェッド流域になります。
- watershed_linebool, オプション
Trueの場合、ウォーターシェッドアルゴリズムによって得られた領域を1ピクセル幅の線で区切ります。この線にはラベル0が付けられます。この線を追加するために使用される方法は、マーカー領域が隣接していないことを想定していることに注意してください。ウォーターシェッド線は、隣接するマーカー領域間の境界を捉えない場合があります。
- 戻り値:
- outndarray
markersと同じ型および形状のラベル付き行列。
参照
skimage.segmentation.random_walker異方性拡散に基づくセグメンテーションアルゴリズムで、通常はウォーターシェッドよりも遅いですが、ノイズの多いデータや穴のある境界で優れた結果が得られます。
注
この関数は、マークされた流域にピクセルを割り当てるウォーターシェッドアルゴリズム [2] [3] を実装します。アルゴリズムは、ピクセル値が優先度キューのメトリックであり、次にキューへの入力時間である優先度キューを使用してピクセルを保持します。これにより、最も近いマーカーが優先されます。
いくつかのアイデアは [4] から引用されています。この論文における最も重要な洞察は、キューへの入力時間で2つの問題を解決できるということです。1つは、ピクセルは最大の勾配を持つ隣接に割り当てられる必要があり、もう1つは、勾配がない場合、プラトー上のピクセルは反対側のマーカー間で分割される必要があるということです。
この実装は、すべての引数を特定の、最小公分母の型に変換し、これらをCアルゴリズムに渡します。
マーカーは手動で決定することも、例えば画像の勾配の局所的な極小値や、重なり合うオブジェクトを分離するための背景までの距離関数の局所的な極大値を用いて自動的に決定することもできます(例を参照)。
参考文献
[1]P. Neubert and P. Protzel, “Compact Watershed and Preemptive SLIC: On Improving Trade-offs of Superpixel Segmentation Algorithms,” 2014 22nd International Conference on Pattern Recognition, Stockholm, Sweden, 2014, pp. 996-1001, DOI:10.1109/ICPR.2014.181 https://www.tu-chemnitz.de/etit/proaut/publications/cws_pSLIC_ICPR.pdf
[4]P. J. Soille and M. M. Ansoult, “Automated basin delineation from digital elevation models using mathematical morphology,” Signal Processing, 20(2):171-182, DOI:10.1016/0165-1684(90)90127-K
例
ウォーターシェッドアルゴリズムは、重なり合うオブジェクトを分離するのに役立ちます。
まず、2つの重なり合う円を持つ初期画像を生成します。
>>> x, y = np.indices((80, 80)) >>> x1, y1, x2, y2 = 28, 28, 44, 52 >>> r1, r2 = 16, 20 >>> mask_circle1 = (x - x1)**2 + (y - y1)**2 < r1**2 >>> mask_circle2 = (x - x2)**2 + (y - y2)**2 < r2**2 >>> image = np.logical_or(mask_circle1, mask_circle2)
次に、2つの円を分離したいとします。背景までの距離の極大値にマーカーを生成します。
>>> from scipy import ndimage as ndi >>> distance = ndi.distance_transform_edt(image) >>> from skimage.feature import peak_local_max >>> max_coords = peak_local_max(distance, labels=image, ... footprint=np.ones((3, 3))) >>> local_maxima = np.zeros_like(image, dtype=bool) >>> local_maxima[tuple(max_coords.T)] = True >>> markers = ndi.label(local_maxima)[0]
最後に、画像とマーカーに対してウォーターシェッドを実行します。
>>> labels = watershed(-distance, markers, mask=image)
このアルゴリズムは3D画像にも適用でき、例えば重なり合う球を分離するために使用できます。