skimage.restoration#
復元アルゴリズム、例えば、デコンボリューションアルゴリズム、ノイズ除去など。
復元用のボールカーネルを作成します。rolling_ball。 |
|
ノイズ除去関数を調整し、最適なJ不変バージョンを返します。 |
|
サイクルスピン(xのシフトされたバージョンにfuncを繰り返し適用します)。 |
|
バイラテラルフィルターを使用して画像をノイズ除去します。 |
|
ノイズ除去関数のJ不変バージョンを適用します。 |
|
2D〜4DグレースケールまたはRGB画像で非ローカルミーンズノイズ除去を実行します。 |
|
分割ブレグマン最適化を使用して全変動ノイズ除去を実行します。 |
|
nDで全変動ノイズ除去を実行します。 |
|
画像にウェーブレットノイズ除去を実行します。 |
|
復元用の楕円体カーネルを作成します。rolling_ball。 |
|
(ガウス)ノイズの標準偏差のロバストなウェーブレットベースの推定器。 |
|
画像のマスクされた点を双調和方程式でインペイントします。 |
|
リチャードソン-ルーシーのデコンボリューション。 |
|
カーネルを回転/移動して背景強度を推定します。 |
|
教師なしウィーナー-ハントのデコンボリューション。 |
|
折り返された位相画像からオリジナルを復元します。 |
|
ウィーナー-ハントのデコンボリューション |
- skimage.restoration.ball_kernel(radius, ndim)[ソース]#
復元用のボールカーネルを作成します。rolling_ball。
- パラメーター:
- radiusint
ボールの半径。
- ndimint
ボールの次元数。
ndimは、カーネルが適用される画像の次元数と一致する必要があります。
- 戻り値:
- kernelndarray
楕円体の上半分の表面強度を含むカーネル。
参考
- skimage.restoration.calibrate_denoiser(image, denoise_function, denoise_parameters, *, stride=4, approximate_loss=True, extra_output=False)[ソース]#
ノイズ除去関数を調整し、最適なJ不変バージョンを返します。
返された関数は、入力画像のノイズ除去に最適なパラメータ値が設定されて部分的に評価されます。
- パラメーター:
- imagendarray
ノイズ除去される入力データ(
img_as_floatを使用して変換されます)。- denoise_functionfunction
調整するノイズ除去関数。
- denoise_parametersリストの辞書
denoise_functionで調整するパラメータの範囲。- strideint, optional
denoise_functionをJ不変に変換するマスキング手順で使用されるストライド。- approximate_lossbool, optional
画像のマスクされた1つのバージョンでのみ計算することで、ノイズ除去器を評価するために使用される自己教師あり損失を近似するかどうか。Falseの場合、実行時間は
stride**image.ndim倍長くなります。- extra_outputbool, optional
Trueの場合、調整されたノイズ除去関数に加えて、パラメータと損失も返します
- 戻り値:
- best_denoise_functionfunction
denoise_functionの最適なJ不変バージョン。extra_outputがTrueの場合、次のタプルも返されます- (parameters_tested, losses)タプル(辞書のリスト、intのリスト)
denoise_functionに対してテストされたパラメータのリスト。kwargsの辞書としてparameters_testedの各パラメータセットの自己教師あり損失。
注釈
キャリブレーション手順では、自己教師あり平均二乗誤差損失を使用して、
denoise_functionのJ不変バージョンのパフォーマンスを評価します。自己教師あり損失の最小化は、グラウンドトゥルース損失(つまり、真のMSEエラー)の最小化でもあります[1]。返された関数は、元のノイズ画像、または同様の特性を持つ他の画像で使用できます。- ストライドを大きくすると、
best_denoise_functionのパフォーマンスが向上します 実行時間が増加する犠牲を伴います。キャリブレーションの実行時間には影響しません。
参考文献
[1]J. Batson&L. Royer。Noise2Self:自己監視によるブラインドノイズ除去、機械学習に関する国際会議、p。524-533(2019)。
例
>>> from skimage import color, data >>> from skimage.restoration import denoise_tv_chambolle >>> import numpy as np >>> img = color.rgb2gray(data.astronaut()[:50, :50]) >>> rng = np.random.default_rng() >>> noisy = img + 0.5 * img.std() * rng.standard_normal(img.shape) >>> parameters = {'weight': np.arange(0.01, 0.3, 0.02)} >>> denoising_function = calibrate_denoiser(noisy, denoise_tv_chambolle, ... denoise_parameters=parameters) >>> denoised_img = denoising_function(img)
- skimage.restoration.cycle_spin(x, func, max_shifts, shift_steps=1, num_workers=None, func_kw=None, *, channel_axis=None)[ソース]#
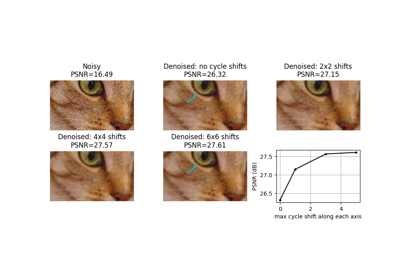
サイクルスピン(xのシフトされたバージョンにfuncを繰り返し適用します)。
- パラメーター:
- x配列のようなオブジェクト
funcへの入力データ。- func関数
円形にシフトされた
xのバージョンに適用する関数。xを最初の引数として取る必要があります。追加の引数は、func_kwを介して指定できます。- max_shiftsintまたはタプル
整数の場合、
range(0, max_shifts+1)のシフトがxの各軸に沿って使用されます。タプルの場合、range(0, max_shifts[i]+1)が軸 i に沿って使用されます。- shift_stepsintまたはタプル、optional
軸iに沿って適用されるシフトのステップサイズは、
range((0, max_shifts[i]+1, shift_steps[i]))です。整数が指定された場合、すべての軸に同じステップサイズが使用されます。- num_workersintまたはNone、optional
サイクルスピン中に使用する並列スレッド数。
Noneに設定すると、使用可能なコアのフルセットが使用されます。- func_kwdict, optional
funcに指定する追加のキーワード引数。- channel_axisintまたはNone、optional
Noneの場合、画像はグレースケール(単一チャネル)画像であると想定されます。それ以外の場合、このパラメーターは、配列のどの軸がチャネルに対応するかを示します。
バージョン0.19で追加:
channel_axisが0.19で追加されました。
- 戻り値:
- avg_ynp.ndarray
指定された軸シフトのすべての組み合わせで平均化された
func(x, **func_kw)の出力。
注釈
サイクルスピンは、シフトバリアント変換のいくつかの循環シフトを実行することによって、シフト不変性にアプローチする方法として提案されました [1]。
nレベルの離散ウェーブレット変換の場合、
max_shifts = 2**n - 1までのすべてのシフトを実行することをお勧めします。実際には、軸ごとのシフト数が少ないだけで、メリットの大部分を実現できることがよくあります。ブロックワイズ離散コサイン変換などの変換の場合、変換で使用されるブロックサイズまでのシフトを評価することをお勧めします。
参考文献
[1]R.R. Coifman と D.L. Donoho。「Translation-Invariant De-Noising」。Wavelets and Statistics、Lecture Notes in Statistics、vol.103。Springer、ニューヨーク、1995年、pp.125-150。DOI:10.1007/978-1-4612-2544-7_9
例
>>> import skimage.data >>> from skimage import img_as_float >>> from skimage.restoration import denoise_tv_chambolle, cycle_spin >>> img = img_as_float(skimage.data.camera()) >>> sigma = 0.1 >>> img = img + sigma * np.random.standard_normal(img.shape) >>> denoised = cycle_spin(img, func=denoise_tv_chambolle, ... max_shifts=3)
- skimage.restoration.denoise_bilateral(image, win_size=None, sigma_color=None, sigma_spatial=1, bins=10000, mode='constant', cval=0, *, channel_axis=None)[ソース]#
バイラテラルフィルターを使用して画像をノイズ除去します。
- パラメーター:
- imagendarray、形状 (M, N[, 3])
入力画像、2DグレースケールまたはRGB。
- win_sizeint
フィルタリングのウィンドウサイズ。win_sizeが指定されていない場合、
max(5, 2 * ceil(3 * sigma_spatial) + 1)として計算されます。- sigma_colorfloat
グレースケール/色距離(放射輝度類似性)の標準偏差。値が大きいほど、放射輝度の差が大きいピクセルが平均化されます。
Noneの場合、imageの標準偏差が使用されます。- sigma_spatialfloat
範囲距離の標準偏差。値が大きいほど、空間的な差が大きいピクセルが平均化されます。
- binsint
色フィルタリングのガウス重みの離散値の数。値が大きいほど、精度が向上します。
- mode{‘constant’, ‘edge’, ‘symmetric’, ‘reflect’, ‘wrap’}
画像の境界外の値を処理する方法。詳細については、
numpy.padを参照してください。- cvalint または float
モード 'constant' と組み合わせて使用され、画像境界外の値です。
- channel_axisintまたはNone、optional
Noneの場合、画像はグレースケール(シングルチャネル)と見なされます。それ以外の場合、このパラメータは、配列のどの軸がチャネルに対応するかを示します。バージョン0.19で追加:
channel_axisが0.19で追加されました。
- 戻り値:
- denoisedndarray
ノイズ除去された画像。
注釈
これはエッジ保持型のノイズ除去フィルターです。空間的な近さと放射輝度の類似性に基づいてピクセルを平均化します[1]。
空間的な近さは、2つのピクセル間のユークリッド距離と特定の標準偏差(
sigma_spatial)のガウス関数によって測定されます。放射輝度の類似性は、2つの色値間のユークリッド距離と特定の標準偏差(
sigma_color)のガウス関数によって測定されます。画像が任意の
intdtypeである場合、imageはimg_as_float関数を使用して変換されるため、標準偏差(sigma_color)は[0, 1]の範囲になります。scikit-imageのデータ型変換と、これらの変換で画像がどのようにリスケールされるかについての詳細は、https://scikit-image.dokyumento.jp/docs/stable/user_guide/data_types.html を参照してください。
参考文献
[1]C. Tomasi および R. Manduchi。「グレースケールおよびカラー画像のためのバイラテラルフィルタリング。」IEEE International Conference on Computer Vision (1998) 839-846。DOI:10.1109/ICCV.1998.710815
例
>>> from skimage import data, img_as_float >>> astro = img_as_float(data.astronaut()) >>> astro = astro[220:300, 220:320] >>> rng = np.random.default_rng() >>> noisy = astro + 0.6 * astro.std() * rng.random(astro.shape) >>> noisy = np.clip(noisy, 0, 1) >>> denoised = denoise_bilateral(noisy, sigma_color=0.05, sigma_spatial=15, ... channel_axis=-1)
- skimage.restoration.denoise_invariant(image, denoise_function, *, stride=4, masks=None, denoiser_kwargs=None)[ソース]#
ノイズ除去関数のJ不変バージョンを適用します。
- パラメーター:
- imagendarray (M[, N[, …]][, C])、int、uint、または float
ノイズ除去される入力データ。
imageは任意の数値型にできますが、ノイズ除去された画像の計算のためにfloatのndarrayにキャストされます(img_as_floatを使用)。- denoise_functionfunction
元のノイズ除去関数。
- strideint, optional
denoise_functionをJ不変に変換するマスキング手順で使用されるストライド。- masksndarray のリスト、オプション
J不変出力を計算するために使用するマスクのセット。
Noneの場合、画像をカバーするマスクのフルセットが使用されます。- denoiser_kwargs
denoise_functionに渡されるキーワード引数。
- 戻り値:
- outputndarray
ノイズ除去された画像、
imageと同じ形状。
注釈
ノイズ除去関数は、各ピクセルの予測が元の画像のそのピクセルの値に依存しない場合、J不変です。各ピクセルの予測は、代わりに画像の残りの部分に含まれるすべての関連情報を使用する場合があります。これは通常、非常に重要です。任意の関数は、[1]で説明されている単純なマスキング手順を使用して、J不変に変換できます。
各ピクセルのノイズが独立している限り、J不変ノイズ除去のピクセル単位の誤差はノイズと相関していません。その結果、ノイズ除去された画像とノイズの多い画像間の平均差である自己教師あり損失は、ノイズ除去された画像と元のクリーンな画像間の差であるグランドトゥルース損失と同じです(定数まで)。
これは、ノイズの多いデータのみを使用して、自己教師あり損失を最小化するノイズ除去を選択することにより、特定の画像に最適なJ不変ノイズ除去を見つけることができることを意味します。
参考文献
[1]J. Batson&L. Royer。Noise2Self:自己監視によるブラインドノイズ除去、機械学習に関する国際会議、p。524-533(2019)。
例
>>> import skimage >>> from skimage.restoration import denoise_invariant, denoise_tv_chambolle >>> image = skimage.util.img_as_float(skimage.data.chelsea()) >>> noisy = skimage.util.random_noise(image, var=0.2 ** 2) >>> denoised = denoise_invariant(noisy, denoise_function=denoise_tv_chambolle)
- skimage.restoration.denoise_nl_means(image, patch_size=7, patch_distance=11, h=0.1, fast_mode=True, sigma=0.0, *, preserve_range=False, channel_axis=None)[ソース]#
2D〜4DグレースケールまたはRGB画像で非ローカルミーンズノイズ除去を実行します。
- パラメーター:
- image2D または 3D ndarray
ノイズ除去される入力画像。2Dまたは3D、およびグレースケールまたはRGB(2D画像のみ、
channel_axisパラメータを参照)にできます。任意の数のチャネル(厳密にはRGBである必要はありません)にできます。- patch_sizeint、オプション
ノイズ除去に使用されるパッチのサイズ。
- patch_distanceint、オプション
ノイズ除去に使用されるパッチを検索するピクセル単位の最大距離。
- hfloat、オプション
カットオフ距離(グレースケールレベル)。hが高いほど、パッチの受け入れに寛容になります。hが高いほど、機能がぼやける代わりに、画像が滑らかになります。標準偏差sigmaのガウスノイズの場合、hの値をわずかに少ないsigmaに選択するのが経験則です。
- fast_modebool、オプション
True(デフォルト値)の場合、非ローカル平均アルゴリズムの高速バージョンが使用されます。Falseの場合、非ローカル平均の元のバージョンが使用されます。アルゴリズムの詳細については、注記セクションを参照してください。
- sigmafloat、オプション
(ガウス)ノイズの標準偏差。指定した場合、予想されるノイズ分散を考慮した、より堅牢なパッチ重みの計算が行われます(以下の注記を参照)。
- preserve_rangebool、オプション
元の値の範囲を維持するかどうか。それ以外の場合、入力画像は
img_as_floatの規則に従って変換されます。https://scikit-image.dokyumento.jp/docs/dev/user_guide/data_types.html も参照してください- channel_axisintまたはNone、optional
Noneの場合、画像はグレースケール(単一チャネル)画像であると想定されます。それ以外の場合、このパラメーターは、配列のどの軸がチャネルに対応するかを示します。
バージョン0.19で追加:
channel_axisが0.19で追加されました。
- 戻り値:
- resultndarray
ノイズ除去された画像、
imageと同じ形状。
注釈
非ローカル平均アルゴリズムは、特定のテクスチャを持つ画像のノイズ除去に適しています。アルゴリズムの原理は、他のピクセルを中心としたパッチが、目的のピクセルを中心としたパッチと十分に類似している場合に、制限された近傍内の他のピクセルの値と特定のピクセルの値を平均化することです。
オリジナルのアルゴリズムのバージョン(
fast=Falseに対応)[1]では、計算量は次のようになります。image.size * patch_size ** image.ndim * patch_distance ** image.ndim
したがって、パッチのサイズや最大距離を変更すると、特に3D画像の場合、計算時間に大きな影響があります。
ただし、デフォルトの動作は
fast_mode=Trueに対応しており、その場合、非局所平均の別のバージョン[2]が使用され、計算量は次のようになります。image.size * patch_distance ** image.ndim
計算時間は、特定のシフトにおけるパッチ距離の積分計算のおかげで、操作回数が減り[1]、パッチサイズにあまり依存しません。したがって、このアルゴリズムは、2倍のメモリを使用する代わりに、クラシックなアルゴリズム(
fast_mode=False)よりも高速に実行されます。この実装は、他の代替案と比較してより効率的であることが証明されています。例えば、[3]を参照してください。クラシックなアルゴリズムと比較して、パッチ内のすべてのピクセルは、パッチの中心からの距離に関係なく、同じ重みで別のパッチとの距離に寄与します。このより粗い距離計算は、わずかに低いノイズ除去性能につながる可能性があります。さらに、小さな画像(線形サイズがパッチサイズの数倍しかない画像)の場合、境界効果により、クラシックなアルゴリズムの方が速くなる場合があります。
画像は、ノイズ除去前に
skimage.util.padのreflectモードを使用してパディングされます。ノイズの標準偏差である
sigmaが提供されている場合は、パッチの重みのよりロバストな計算が使用されます。計算されたパッチ距離から既知のノイズ分散を差し引くことで、パッチの類似性の推定が改善され、ノイズ除去性能が適度に向上します[4]。これは、[3]でアルゴリズムの高速バリアントのオプションとしても言及されました。sigmaが提供されている場合は、オーバー スムージングを避けるために、通常、より小さなhを使用する必要があります。hの最適な値は、画像の内容とノイズ レベルに依存しますが、fast_modeがTrueの場合はh = 0.8 * sigma、fast_modeがFalseの場合はh = 0.6 * sigmaが妥当な開始点です。参考文献
[1] (1,2)A. Buades, B. Coll, & J-M. Morel. A non-local algorithm for image denoising. In CVPR 2005, Vol. 2, pp. 60-65, IEEE. DOI:10.1109/CVPR.2005.38
[2]J. Darbon, A. Cunha, T.F. Chan, S. Osher, and G.J. Jensen, Fast nonlocal filtering applied to electron cryomicroscopy, in 5th IEEE International Symposium on Biomedical Imaging: From Nano to Macro, 2008, pp. 1331-1334. DOI:10.1109/ISBI.2008.4541250
[3] (1,2)Jacques Froment. Parameter-Free Fast Pixelwise Non-Local Means Denoising. Image Processing On Line, 2014, vol. 4, pp. 300-326. DOI:10.5201/ipol.2014.120
[4]A. Buades, B. Coll, & J-M. Morel. Non-Local Means Denoising. Image Processing On Line, 2011, vol. 1, pp. 208-212. DOI:10.5201/ipol.2011.bcm_nlm
例
>>> a = np.zeros((40, 40)) >>> a[10:-10, 10:-10] = 1. >>> rng = np.random.default_rng() >>> a += 0.3 * rng.standard_normal(a.shape) >>> denoised_a = denoise_nl_means(a, 7, 5, 0.1)
- skimage.restoration.denoise_tv_bregman(image, weight=5.0, max_num_iter=100, eps=0.001, isotropic=True, *, channel_axis=None)[source]#
分割ブレグマン最適化を使用して全変動ノイズ除去を実行します。
与えられたノイズの多い画像(入力データ)\(f\)に対して、全変動ノイズ除去(全変動正則化としても知られています)は、\(f\)よりも全変動が少ない画像\(u\)を、\(u\)が\(f\)と類似したままであるという制約の下で発見することを目的とします。これは、ルーディン-オシャー-ファテミ(ROF)最小化問題で表すことができます。
\[\min_{u} \sum_{i=0}^{N-1} \left( \left| \nabla{u_i} \right| + \frac{\lambda}{2}(f_i - u_i)^2 \right)\]ここで、\(\lambda\)は正のパラメータです。このコスト関数の最初の項は全変動であり、2番目の項はデータ忠実度を表します。\(\lambda \to 0\)の場合、全変動項が支配的になり、入力データのように見えることを犠牲にして、解がより小さな全変動を持つように強制されます。
このコードは、ROF問題を解決するための、ゴールドスタインとオシャーの分割ブレグマンアルゴリズムの実装です([1]、[2]、[3])。
- パラメーター:
- imagendarray
img_as_float()を使用して変換された、ノイズ除去される入力画像。- weightfloat、オプション
ノイズ除去の重み。\(\frac{\lambda}{2}\)に等しくなります。したがって、
weightが小さいほど、ノイズ除去が多くなります(imageとの類似性が低下します)。- epsfloat、オプション
停止基準の許容誤差 \(\varepsilon > 0\):アルゴリズムは \(\|u_n - u_{n-1}\|_2 < \varepsilon\) のときに停止します。
- max_num_iterint、オプション
最適化に使用される最大反復回数。
- isotropicboolean、オプション
等方性TVノイズ除去と異方性TVノイズ除去を切り替えます。
- channel_axisintまたはNone、optional
Noneの場合、画像はグレースケール(シングルチャネル)と見なされます。それ以外の場合、このパラメータは、配列のどの軸がチャネルに対応するかを示します。バージョン0.19で追加:
channel_axisが0.19で追加されました。
- 戻り値:
- undarray
ノイズ除去された画像。
参考
denoise_tv_chambollenDで全変動ノイズ除去を実行します。
注釈
カラー画像では、
channel_axisパラメータが適切に設定されていることを確認してください。全変動ノイズ除去の原則は、[4]で説明されています。これは、画像の勾配のノルムの積分としておおまかに記述できる、画像の全変動を最小化することです。全変動ノイズ除去は、区分的に一定の画像である、漫画のような画像を生成する傾向があります。
参考文献
[1]Tom Goldstein and Stanley Osher, “The Split Bregman Method For L1 Regularized Problems”, https://ww3.math.ucla.edu/camreport/cam08-29.pdf
[2]Pascal Getreuer, “Rudin–Osher–Fatemi Total Variation Denoising using Split Bregman” in Image Processing On Line on 2012–05–19, https://www.ipol.im/pub/art/2012/g-tvd/article_lr.pdf
- skimage.restoration.denoise_tv_chambolle(image, weight=0.1, eps=0.0002, max_num_iter=200, *, channel_axis=None)[source]#
nDで全変動ノイズ除去を実行します。
与えられたノイズの多い画像(入力データ)\(f\)に対して、全変動ノイズ除去(全変動正則化としても知られています)は、\(f\)よりも全変動が少ない画像\(u\)を、\(u\)が\(f\)と類似したままであるという制約の下で発見することを目的とします。これは、ルーディン-オシャー-ファテミ(ROF)最小化問題で表すことができます。
\[\min_{u} \sum_{i=0}^{N-1} \left( \left| \nabla{u_i} \right| + \frac{\lambda}{2}(f_i - u_i)^2 \right)\]ここで、\(\lambda\)は正のパラメータです。このコスト関数の最初の項は全変動であり、2番目の項はデータ忠実度を表します。\(\lambda \to 0\)の場合、全変動項が支配的になり、入力データのように見えることを犠牲にして、解がより小さな全変動を持つように強制されます。
このコードは、ROF問題を解決するために、[1]のシャンボールによって提案されたアルゴリズムの実装です。
- パラメーター:
- imagendarray
ノイズ除去される入力画像。dtypeがfloatでない場合は、
img_as_float()で変換されます。- weightfloat、オプション
ノイズ除去の重み。これは\(\frac{1}{\lambda}\)に等しい。したがって、
weightが大きいほど、ノイズ除去の効果が高くなる(ただし、imageへの忠実度は犠牲になる)。- epsfloat、オプション
停止基準の許容誤差\(\varepsilon > 0\)(コスト関数\(E\)の相対差の絶対値と比較):アルゴリズムは、\(|E_{n-1} - E_n| < \varepsilon * E_0\)になったときに停止する。
- max_num_iterint、オプション
最適化に使用される最大反復回数。
- channel_axisintまたはNone、optional
Noneの場合、画像はグレースケール(シングルチャネル)と見なされます。それ以外の場合、このパラメータは、配列のどの軸がチャネルに対応するかを示します。バージョン0.19で追加:
channel_axisが0.19で追加されました。
- 戻り値:
- undarray
ノイズ除去された画像。
参考
denoise_tv_bregman分割ブレグマン最適化を使用して全変動ノイズ除去を実行します。
注釈
カラー画像の場合は、
channel_axisパラメータを適切に設定するようにしてください。全変動ノイズ除去の原理は、[2]で説明されています。これは、画像の全変動(画像勾配のノルムの積分として大まかに記述できる)を最小化することです。全変動ノイズ除去は、区分的に一定の画像、つまり漫画のような画像を生成する傾向があります。
参考文献
[1]A. Chambolle, An algorithm for total variation minimization and applications, Journal of Mathematical Imaging and Vision, Springer, 2004, 20, 89-97.
例
宇宙飛行士の画像に関する2Dの例
>>> from skimage import color, data >>> img = color.rgb2gray(data.astronaut())[:50, :50] >>> rng = np.random.default_rng() >>> img += 0.5 * img.std() * rng.standard_normal(img.shape) >>> denoised_img = denoise_tv_chambolle(img, weight=60)
合成データに関する3Dの例
>>> x, y, z = np.ogrid[0:20, 0:20, 0:20] >>> mask = (x - 22)**2 + (y - 20)**2 + (z - 17)**2 < 8**2 >>> mask = mask.astype(float) >>> rng = np.random.default_rng() >>> mask += 0.2 * rng.standard_normal(mask.shape) >>> res = denoise_tv_chambolle(mask, weight=100)
- skimage.restoration.denoise_wavelet(image, sigma=None, wavelet='db1', mode='soft', wavelet_levels=None, convert2ycbcr=False, method='BayesShrink', rescale_sigma=True, *, channel_axis=None)[source]#
画像にウェーブレットノイズ除去を実行します。
- パラメーター:
- imagendarray (M[, N[, …P]][, C])、整数、符号なし整数、または浮動小数点数
ノイズ除去する入力データ。
imageは任意の数値型にできますが、ノイズ除去された画像の計算のために浮動小数点数のndarrayにキャストされます。- sigmafloatまたはlist、オプション
ウェーブレット詳細係数のしきい値を計算するときに使用されるノイズ標準偏差。None(デフォルト)の場合、ノイズ標準偏差は[2]の方法で推定されます。
- waveletstring、オプション
実行するウェーブレットの種類。
pywt.wavelistが出力するオプションのいずれかを使用できます。デフォルトは'db1'です。たとえば、waveletは、{'db2', 'haar', 'sym9'}などの多くの値のいずれかになります。- mode{'soft', 'hard'}、オプション
実行するノイズ除去の種類を選択するオプションの引数。加法性ノイズが与えられた場合、ソフトしきい値処理を選択すると、元の画像の最適な近似値が見つかることに注意してください。
- wavelet_levelsintまたはNone、オプション
使用するウェーブレット分解レベルの数。デフォルトは、可能な最大分解レベル数より3つ少ない値です。
- convert2ycbcrbool、オプション
Trueでchannel_axisが設定されている場合、RGBカラースペースではなくYCbCrカラースペースでウェーブレットノイズ除去を行います。これにより、通常、RGB画像のパフォーマンスが向上します。
- method{'BayesShrink', 'VisuShrink'}、オプション
使用するしきい値処理方法。現在サポートされている方法は、「BayesShrink」[1]と「VisuShrink」[2]です。デフォルトは「BayesShrink」です。
- rescale_sigmabool、オプション
Falseの場合、ユーザーが指定した
sigmaのリスケールは実行されません。デフォルトのTrueは、画像が内部的にリスケールされる場合に、sigmaを適切にリスケールします。バージョン0.16で追加:
rescale_sigmaは0.16で導入されました- channel_axisintまたはNone、optional
Noneの場合、画像はグレースケール(シングルチャネル)と見なされます。それ以外の場合、このパラメータは、配列のどの軸がチャネルに対応するかを示します。バージョン0.19で追加:
channel_axisが0.19で追加されました。
- 戻り値:
- outndarray
ノイズ除去された画像。
注釈
ウェーブレットドメインは画像のスパース表現であり、フーリエ変換の周波数ドメインと同様に考えることができます。スパース表現はほとんどの値がゼロまたはゼロに近い値であり、真にランダムなノイズは(通常)ウェーブレットドメインの多くの小さい値で表されます。一部のしきい値より下のすべての値を0に設定すると、画像のノイズが軽減されますが、しきい値が大きいほど画像に存在する詳細も減少します。
入力が3Dの場合、この関数は各カラープレーンで個別にウェーブレットノイズ除去を実行します。
バージョン0.16で変更: 浮動小数点入力の場合、元の入力範囲が維持され、出力にクリッピングは適用されません。他の入力タイプは、入力画像範囲に応じて[-1, 1]または[0, 1]の範囲の浮動小数点値に変換されます。
rescale_sigma = Falseでない限り、imageに適用される内部リスケールは、同じ相対振幅を維持するためにsigmaにも適用されます。多くのウェーブレット係数しきい値処理アプローチが提案されています。デフォルトでは、
denoise_waveletは、[1]で説明されているように、各ウェーブレットサブバンドの個別のしきい値を計算する適応しきい値処理方法であるBayesShrinkを適用します。method == "VisuShrink"の場合、[2]で説明されているように、単一の「ユニバーサルしきい値」がすべてのウェーブレット詳細係数に適用されます。このしきい値は、指定されたsigmaで、すべてのガウスノイズを高い確率で除去するように設計されていますが、過度に滑らかに見える画像を生成する傾向があります。PyWaveletsのウェーブレットはどれでも選択できますが、しきい値処理方法は直交ウェーブレット変換を想定しており、双直交ウェーブレットに対してしきい値を適切に選択できない場合があります。入力のホワイトノイズがサブバンドでもホワイトノイズのままであるため、直交ウェーブレットが望ましいです。双直交ウェーブレットはサブバンドで色付きのノイズにつながります。さらに、PyWaveletsの直交ウェーブレットは正規直交であるため、サブバンドのノイズ分散は入力のノイズ分散と同じままです。直交ウェーブレットの例としては、Daubechies(例:’db2’)またはsymmlet(例:’sym2’)ファミリがあります。参考文献
[1] (1,2)Chang, S. Grace, Bin Yu, and Martin Vetterli. “Adaptive wavelet thresholding for image denoising and compression.” Image Processing, IEEE Transactions on 9.9 (2000): 1532-1546. DOI:10.1109/83.862633
[2] (1,2,3)D. L. Donoho and I. M. Johnstone. “Ideal spatial adaptation by wavelet shrinkage.” Biometrika 81.3 (1994): 425-455. DOI:10.1093/biomet/81.3.425
例
>>> from skimage import color, data >>> img = img_as_float(data.astronaut()) >>> img = color.rgb2gray(img) >>> rng = np.random.default_rng() >>> img += 0.1 * rng.standard_normal(img.shape) >>> img = np.clip(img, 0, 1) >>> denoised_img = denoise_wavelet(img, sigma=0.1, rescale_sigma=True)
- skimage.restoration.ellipsoid_kernel(shape, intensity)[source]#
復元用の楕円体カーネルを作成します。rolling_ball。
- パラメーター:
- shapearray-like
楕円の主軸の長さ(強度軸を除く)。カーネルは、適用される画像と同じ次元数を持つ必要があります。
- intensityint
楕円の強度軸の長さ。
- 戻り値:
- kernelndarray
楕円体の上半分の表面強度を含むカーネル。
参考
- skimage.restoration.estimate_sigma(image, average_sigmas=False, *, channel_axis=None)[source]#
(ガウス)ノイズの標準偏差のロバストなウェーブレットベースの推定器。
- パラメーター:
- imagendarray
ノイズ標準偏差を推定する画像。
- average_sigmasbool、オプション
trueの場合、
sigmaのチャネル推定値を平均します。それ以外の場合は、各チャネルに対応するsigmaのリストを返します。- channel_axisintまたはNone、optional
Noneの場合、画像はグレースケール(シングルチャネル)と見なされます。それ以外の場合、このパラメータは、配列のどの軸がチャネルに対応するかを示します。バージョン0.19で追加:
channel_axisが0.19で追加されました。
- 戻り値:
- sigmafloatまたはlist
推定されたノイズ標準偏差。
multichannelがTrueで、average_sigmasがFalseの場合、各チャネルの個別のノイズ推定が返されます。それ以外の場合は、個々のチャネル推定値の平均が返されます。
注釈
この関数は、ノイズがガウス分布に従うことを想定しています。推定アルゴリズムは、[1]のセクション4.2で説明されているように、ウェーブレット詳細係数の中央絶対偏差に基づいています。
参考文献
[1]D. L. Donoho and I. M. Johnstone. “Ideal spatial adaptation by wavelet shrinkage.” Biometrika 81.3 (1994): 425-455. DOI:10.1093/biomet/81.3.425
例
>>> import skimage.data >>> from skimage import img_as_float >>> img = img_as_float(skimage.data.camera()) >>> sigma = 0.1 >>> rng = np.random.default_rng() >>> img = img + sigma * rng.standard_normal(img.shape) >>> sigma_hat = estimate_sigma(img, channel_axis=None)
- skimage.restoration.inpaint_biharmonic(image, mask, *, split_into_regions=False, channel_axis=None)[source]#
画像のマスクされた点を双調和方程式でインペイントします。
- パラメーター:
- image(M[, N[, …, P]][, C]) ndarray
入力画像。
- mask(M[, N[, …, P]]) ndarray
インペイントされるピクセルの配列。’image’チャンネルのいずれかと同じ形状である必要があります。不明なピクセルは1で、既知のピクセルは0で表す必要があります。
- split_into_regionsboolean, optional
Trueの場合、インペイントは領域ごとに行われます。これは遅くなる可能性がありますが、メモリ要件が少なくなります。
- channel_axisintまたはNone、optional
Noneの場合、画像はグレースケール(単一チャネル)画像であると想定されます。それ以外の場合、このパラメーターは、配列のどの軸がチャネルに対応するかを示します。
バージョン0.19で追加:
channel_axisが0.19で追加されました。
- 戻り値:
- out(M[, N[, …, P]][, C]) ndarray
マスクされたピクセルがインペイントされた入力画像。
参考文献
[1]S.B.Damelin and N.S.Hoang. “On Surface Completion and Image Inpainting by Biharmonic Functions: Numerical Aspects”, International Journal of Mathematics and Mathematical Sciences, Vol. 2018, Article ID 3950312 DOI:10.1155/2018/3950312
[2]C. K. Chui and H. N. Mhaskar, MRA Contextual-Recovery Extension of Smooth Functions on Manifolds, Appl. and Comp. Harmonic Anal., 28 (2010), 104-113, DOI:10.1016/j.acha.2009.04.004
例
>>> img = np.tile(np.square(np.linspace(0, 1, 5)), (5, 1)) >>> mask = np.zeros_like(img) >>> mask[2, 2:] = 1 >>> mask[1, 3:] = 1 >>> mask[0, 4:] = 1 >>> out = inpaint_biharmonic(img, mask)
- skimage.restoration.richardson_lucy(image, psf, num_iter=50, clip=True, filter_epsilon=None)[source]#
リチャードソン-ルーシーのデコンボリューション。
- パラメーター:
- image([P, ]M, N) ndarray
入力の劣化画像(n次元にできます)。デフォルトの
clip=Trueパラメーターを保持する場合、情報損失を避けるために、画像の値を[-1, 1]の間になるように正規化することをお勧めします。- psfndarray
点拡がり関数。
- num_iterint, optional
反復回数。このパラメーターは正則化の役割を果たします。
- clipboolean, optional
デフォルトではTrue。trueの場合、skimageパイプラインの互換性のために、1を超えるまたは-1未満の結果のピクセル値は閾値処理されます。
- filter_epsilon: float, optional
小さな数による除算を避けるために、中間結果が0になる値。
- 戻り値:
- im_deconvndarray
デコンボリューションされた画像。
参考文献
例
>>> from skimage import img_as_float, data, restoration >>> camera = img_as_float(data.camera()) >>> from scipy.signal import convolve2d >>> psf = np.ones((5, 5)) / 25 >>> camera = convolve2d(camera, psf, 'same') >>> rng = np.random.default_rng() >>> camera += 0.1 * camera.std() * rng.standard_normal(camera.shape) >>> deconvolved = restoration.richardson_lucy(camera, psf, 5)
- skimage.restoration.rolling_ball(image, *, radius=100, kernel=None, nansafe=False, num_threads=None)[source]#
カーネルを回転/移動して背景強度を推定します。
このローリングボールアルゴリズムは、不均一な露光の場合のndimageの背景強度を推定します。これは、頻繁に使用されるローリングボールアルゴリズムの一般化です[1]。
- パラメーター:
- imagendarray
フィルタリングされる画像。
- radiusint, optional
画像内でローリング/並進されるボール形状のカーネルの半径。
kernel = Noneの場合に使用されます。- kernelndarray, optional
画像内でローリング/並進されるカーネル。
imageと同じ次元数である必要があります。カーネルは、その位置でのカーネルの強度で満たされています。- nansafe: bool, optional
False(デフォルト)の場合、imageの値にnp.nanがないと想定し、より高速な実装を使用します。- num_threads: int, optional
使用する最大スレッド数。
Noneの場合、OpenMPのデフォルト値を使用します。通常、仮想コアの最大数と同じです。注:これはスレッド数の上限です。正確な数は、システムのOpenMPライブラリによって決定されます。
- 戻り値:
- backgroundndarray
画像の推定された背景。
注釈
背景強度が推定されたピクセル(一般性を失うことなく
centerで)の場合、ローリングボールメソッドは、カーネルをその下に配置し、サーフェスがいくつかのpos=(y,x)で画像の陰影に接触するまでカーネルを上昇させます。次に、背景強度は、その位置での画像強度(image[pos])と、kernel[center] - kernel[pos]の差を使用して推定されます。このアルゴリズムは、暗いピクセルが背景に対応すると想定しています。明るい背景がある場合は、関数に渡す前に、たとえば
utils.invertを使用して、画像を反転します。詳細については、ギャラリーの例を参照してください。このアルゴリズムはノイズ(特に塩コショウノイズ)に敏感です。これが画像の問題である場合は、この関数に画像を渡す前に、穏やかなガウス平滑化を適用できます。
このアルゴリズムの複雑さは、半径の多項式であり、次数は画像次元(2D画像はN^2、3D画像はN^3など)に等しいため、半径が30を超えると時間がかかる可能性があります([2]、[3])。これは正確なN次元計算です。必要なのが近似だけの場合は、トップハットフィルタリング[4]またはダウンサイズの後にアップサイズして処理される入力のサイズを削減することを検討してください。
参考文献
[1]Sternberg, Stanley R. “Biomedical image processing.” Computer 1 (1983): 22-34. DOI:10.1109/MC.1983.1654163
例
>>> import numpy as np >>> from skimage import data >>> from skimage.restoration import rolling_ball >>> image = data.coins() >>> background = rolling_ball(data.coins()) >>> filtered_image = image - background
>>> import numpy as np >>> from skimage import data >>> from skimage.restoration import rolling_ball, ellipsoid_kernel >>> image = data.coins() >>> kernel = ellipsoid_kernel((101, 101), 75) >>> background = rolling_ball(data.coins(), kernel=kernel) >>> filtered_image = image - background
- skimage.restoration.unsupervised_wiener(image, psf, reg=None, user_params=None, is_real=True, clip=True, *, rng=None)[source]#
教師なしウィーナー-ハントのデコンボリューション。
ハイパーパラメーターが自動的に推定される、ウィーナー・ハントアプローチによるデコンボリューションを返します。このアルゴリズムは、以下の参考文献で説明されている確率的反復プロセス(ギブスサンプラー)です。また、
wiener関数も参照してください。- パラメーター:
- image(M, N) ndarray
入力の劣化画像。
- psfndarray
インパルス応答(入力画像の空間)または伝達関数(フーリエ空間)。両方とも受け入れられます。伝達関数は、自動的に複素数であると認識されます(
np.iscomplexobj(psf))。- regndarray, optional
正則化演算子。デフォルトではラプラシアン。psfと同様に、インパルス応答または伝達関数にすることができます。
- user_paramsdict, optional
ギブスサンプラーのパラメーターのディクショナリー。以下を参照してください。
- clipboolean, optional
デフォルトではTrue。trueの場合、skimageパイプラインの互換性のために、1を超えるまたは-1未満の結果のピクセル値は閾値処理されます。
- rng{
numpy.random.Generator, int}, optional 疑似乱数生成器。デフォルトでは、PCG64ジェネレーターが使用されます(
numpy.random.default_rng()を参照)。rngがintの場合、ジェネレーターのシードに使用されます。バージョン0.19で追加されました。
- 戻り値:
- x_postmean(M, N) ndarray
デコンボリューションされた画像(事後平均)。
- chainsdict
キー
noiseとpriorには、それぞれノイズと事前分布の精度に関するチェーンリストが含まれています。
- その他のパラメータ:
- ``user_params`` のキーは以下のとおりです。
- thresholdfloat
停止基準:連続する近似解(オブジェクトサンプルの経験平均、注記セクション参照)の差のノルム。デフォルトは1e-4です。
- burninint
平均の計算を開始する際に無視するサンプル数。デフォルトは15です。
- min_num_iterint
最小反復回数。デフォルトは30です。
- max_num_iterint
thresholdが満たされない場合の最大反復回数。デフォルトは200です。- callbackcallable (デフォルトはNone)
ユーザーが提供するcallableで、存在する場合は、現在の画像サンプルが渡されます。ユーザーはサンプルを保存したり、平均以外のモーメントを計算したりできます。これはアルゴリズムの実行には影響せず、検査のみを目的としています。
注釈
推定された画像は、確率法則(ベイズ解析に基づく)の事後平均として設計されています。平均は、それぞれの確率で重み付けされたすべての可能な画像に対する合計として定義されます。問題のサイズを考慮すると、正確な合計を処理することはできません。このアルゴリズムでは、事後法則に基づいて画像を描画するためにMCMCを使用します。実際的なアイデアは、平均への寄与が最も大きいため、確率の高い画像のみを描画することです。反対に、確率の低い画像は寄与が小さいため、描画される頻度が少なくなります。最後に、これらのサンプルの経験平均は、平均の推定値と、無限のサンプルセットでの正確な計算を与えます。
参考文献
[1]François Orieux, Jean-François Giovannelli, and Thomas Rodet, “Bayesian estimation of regularization and point spread function parameters for Wiener-Hunt deconvolution”, J. Opt. Soc. Am. A 27, 1593-1607 (2010)
https://www.osapublishing.org/josaa/abstract.cfm?URI=josaa-27-7-1593
例
>>> from skimage import color, data, restoration >>> img = color.rgb2gray(data.astronaut()) >>> from scipy.signal import convolve2d >>> psf = np.ones((5, 5)) / 25 >>> img = convolve2d(img, psf, 'same') >>> rng = np.random.default_rng() >>> img += 0.1 * img.std() * rng.standard_normal(img.shape) >>> deconvolved_img = restoration.unsupervised_wiener(img, psf)
- skimage.restoration.unwrap_phase(image, wrap_around=False, rng=None)[ソース]#
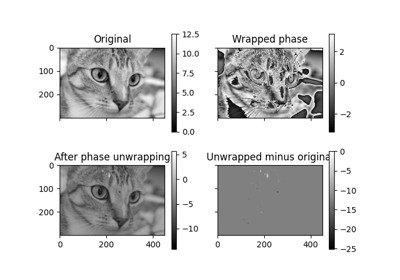
折り返された位相画像からオリジナルを復元します。
[-pi, pi) の範囲にラップされた画像から、元のラップされていない画像を復元します。
- パラメーター:
- image(M[, N[, P]]) floatsのndarrayまたはマスク配列
値は[-pi, pi)の範囲内である必要があります。マスク配列が指定されている場合、マスクされたエントリは変更されず、それらの値は、隣接するマスクされていない値のアンラップをガイドするためには使用されません。マスクされた1次元配列は許可されておらず、
ValueErrorが発生します。- wrap_aroundboolまたはboolのシーケンス(オプション)
シーケンスの要素が
Trueの場合、アンラッププロセスは、画像の対応する軸に沿ったエッジが接続されているとみなし、この接続性を使用して位相アンラッププロセスをガイドします。単一のブール値のみが与えられた場合は、すべての軸に適用されます。1次元配列の場合、ラップアラウンドはサポートされていません。- rng{
numpy.random.Generator, int}, optional 疑似乱数生成器。デフォルトでは、PCG64ジェネレーターが使用されます(
numpy.random.default_rng()を参照)。rngがintの場合、ジェネレーターのシードに使用されます。アンラップはランダムな初期化に依存しています。これにより、決定論的な動作を実現するために使用するPRNGが設定されます。
- 戻り値:
- image_unwrappedarray_like, double
入力と同じ形状のアンラップされた画像。入力
imageがマスク配列であった場合、マスクは保持されます。
- 例外:
- ValueError
マスクされた1次元配列で呼び出された場合、または1次元配列で
wrap_around=Trueで呼び出された場合。
参考文献
[1]Miguel Arevallilo Herraez, David R. Burton, Michael J. Lalor, and Munther A. Gdeisat, “Fast two-dimensional phase-unwrapping algorithm based on sorting by reliability following a noncontinuous path”, Journal Applied Optics, Vol. 41, No. 35 (2002) 7437,
[2]Abdul-Rahman, H., Gdeisat, M., Burton, D., & Lalor, M., “Fast three-dimensional phase-unwrapping algorithm based on sorting by reliability following a non-continuous path. In W. Osten, C. Gorecki, & E. L. Novak (Eds.), Optical Metrology (2005) 32–40, International Society for Optics and Photonics.
例
>>> c0, c1 = np.ogrid[-1:1:128j, -1:1:128j] >>> image = 12 * np.pi * np.exp(-(c0**2 + c1**2)) >>> image_wrapped = np.angle(np.exp(1j * image)) >>> image_unwrapped = unwrap_phase(image_wrapped) >>> np.std(image_unwrapped - image) < 1e-6 # A constant offset is normal True
- skimage.restoration.wiener(image, psf, balance, reg=None, is_real=True, clip=True)[ソース]#
ウィーナー-ハントのデコンボリューション
ウィーナー-ハントアプローチ(つまり、フーリエ対角化)によるデコンボリューションを返します。
- パラメーター:
- imagendarray
入力劣化した画像(n次元でも可)。
- psfndarray
点拡がり関数。データ型が実数の場合はインパルス応答(入力画像空間)とみなされ、データ型が複素数の場合は伝達関数(フーリエ空間)とみなされます。インパルス応答の形状に制約はありません。伝達関数は、
is_realがTrueの場合は(N1, N2, ..., ND)の形状である必要があり、それ以外の場合は(N1, N2, ..., ND // 2 + 1)の形状である必要があります(np.fft.rfftnを参照)。- balancefloat
周波数復元を改善するデータ妥当性と、周波数復元を低減する事前妥当性(ノイズアーチファクトを回避するため)のバランスを調整する正則化パラメータ値。
- regndarray, optional
正則化演算子。デフォルトではラプラシアン。psfと同様に、インパルス応答または伝達関数である可能性があります。形状制約は、
psfパラメータと同じです。- is_realboolean (オプション)
デフォルトはTrue。
psfとregがエルミート仮説で提供されているかどうかを指定します。つまり、周波数面の半分だけが提供されます(実信号のフーリエ変換の冗長性のため)。これは、psfおよび/またはregが伝達関数として提供されている場合にのみ適用されます。エルミートプロパティについては、uftモジュールまたはnp.fft.rfftnを参照してください。- clipboolean, optional
デフォルトはTrue。Trueの場合、1を超えるまたは-1未満の結果のピクセル値は、skimageパイプラインの互換性のためにしきい値処理されます。
- 戻り値:
- im_deconv(M, N) ndarray
デコンボリューションされた画像。
注釈
この関数は、インパルス応答(またはPSF)によってノイズが混入して劣化した画像にウィーナーフィルターを適用します。データモデルが
\[y = Hx + n\]ここで、\(n\)はノイズ、\(H\)はPSF、\(x\)は未知の元の画像である場合、ウィーナーフィルターは
\[\hat x = F^\dagger \left( |\Lambda_H|^2 + \lambda |\Lambda_D|^2 \right)^{-1} \Lambda_H^\dagger F y\]ここで、\(F\)と\(F^\dagger\)はそれぞれフーリエ変換と逆フーリエ変換、\(\Lambda_H\)は伝達関数(またはPSFのフーリエ変換、以下の[Hunt]を参照)、\(\Lambda_D\)は復元された画像の周波数をペナルティを課すフィルターです(デフォルトではラプラシアン、つまり高周波のペナルティ)。パラメータ\(\lambda\)は、データ(ノイズに由来するものであっても、高周波を増加させる傾向がある)と、正則化のバランスを調整します。
これらの方法は、事前のモデルに固有です。したがって、アプリケーションまたは真の画像の性質は、事前のモデルに対応している必要があります。デフォルトでは、事前のモデル(ラプラシアン)は、画像の滑らかさまたはピクセル相関を導入します。これは、データに対する解の不安定性を補償するための高周波ペナルティとして解釈することもできます(ノイズ増幅または「爆発的」解と呼ばれることもあります)。
最後に、フーリエ空間の使用は、\(H\)の巡回プロパティを意味します。 [2]を参照してください。
参考文献
[1]François Orieux, Jean-François Giovannelli, and Thomas Rodet, “Bayesian estimation of regularization and point spread function parameters for Wiener-Hunt deconvolution”, J. Opt. Soc. Am. A 27, 1593-1607 (2010)
https://www.osapublishing.org/josaa/abstract.cfm?URI=josaa-27-7-1593
[2]B. R. Hunt “A matrix theory proof of the discrete convolution theorem”, IEEE Trans. on Audio and Electroacoustics, vol. au-19, no. 4, pp. 285-288, dec. 1971
例
>>> from skimage import color, data, restoration >>> img = color.rgb2gray(data.astronaut()) >>> from scipy.signal import convolve2d >>> psf = np.ones((5, 5)) / 25 >>> img = convolve2d(img, psf, 'same') >>> rng = np.random.default_rng() >>> img += 0.1 * img.std() * rng.standard_normal(img.shape) >>> deconvolved_img = restoration.wiener(img, psf, 0.1)