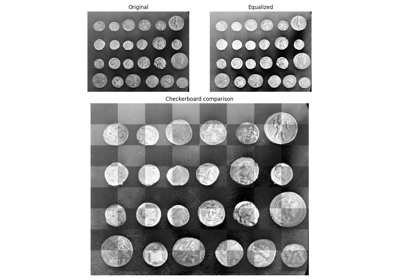
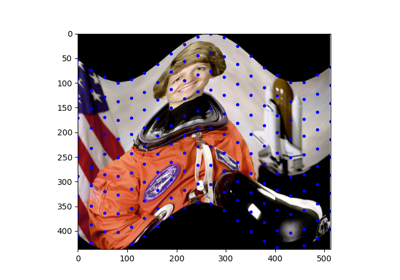
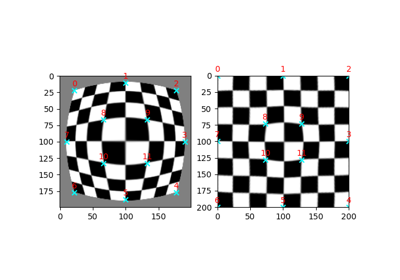
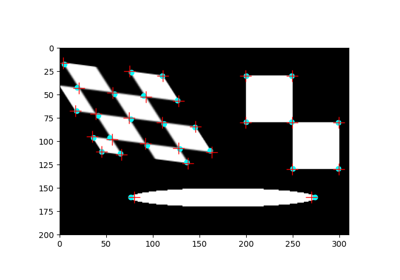
skimage.transform#
幾何学的変換やその他の変換(回転、ラドン変換など)。
幾何学的変換:これらの変換は、画像の形状や位置を変更します。画像の位置合わせ、アラインメント、幾何学的補正などのタスクに役立ちます。例:
AffineTransform、ProjectiveTransform、EuclideanTransform。画像のリサイズとリスケール:これらの変換は、画像のサイズまたは解像度を変更します。画像のサイズを縮小するためにダウンサンプリングしたり、解像度を上げるためにアップサンプリングしたりするタスクに役立ちます。例:
resize()、rescale()。特徴検出と抽出:これらの変換は、画像内の特定の機能やパターンを識別して抽出します。オブジェクト検出、画像セグメンテーション、特徴マッチングなどのタスクに役立ちます。例:
hough_circle()、pyramid_expand()、radon()。画像変換:これらの変換は、コンテンツを変更せずに画像の外観を変更します。画像モザイクの作成、アーティスティックエフェクトの適用、画像データの視覚化などのタスクに役立ちます。例:
warp()、iradon()。
局所平均によるN次元画像のダウンサンプリング。 |
|
2D幾何変換パラメータを推定します。 |
|
入力配列の2次元有限ラドン変換(FRT)を計算します。 |
|
円形ハフ変換を実行します。 |
|
円形ハフ変換のピークを返します。 |
|
楕円ハフ変換を実行します。 |
|
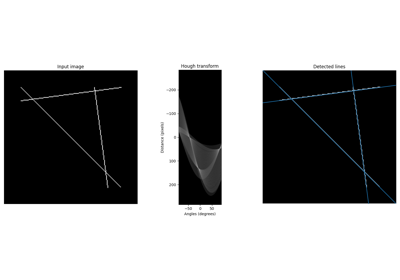
直線ハフ変換を実行します。 |
|
直線ハフ変換のピークを返します。 |
|
入力配列の2次元逆有限ラドン変換(iFRT)を計算します。 |
|
積分画像/総和領域テーブル。 |
|
積分画像を使用して、指定されたウィンドウで積分します。 |
|
逆ラドン変換。 |
|
逆ラドン変換。 |
|
2Dマトリックス変換を適用します。 |
|
後続の投影における相関情報の量を減らすために角度を順序付けます。 |
|
進行的な確率的線ハフ変換から線を返します。 |
|
画像をアップサンプリングしてから平滑化します。 |
|
入力画像によって形成されたガウスピラミッドの画像を生成します。 |
|
入力画像によって形成されたラプラシアンピラミッドの画像を生成します。 |
|
画像を平滑化してからダウンサンプリングします。 |
|
指定された投影角度で画像のラドン変換を計算します。 |
|
画像を特定の係数でスケーリングします。 |
|
画像を特定のサイズにリサイズします。 |
|
局所平均/双一次スケーリングで配列をリサイズします。 |
|
画像の中心を基準にして、画像を特定の角度で回転させます。 |
|
渦巻き変換を実行します。 |
|
指定された座標変換に従って画像をワープします。 |
|
2D画像ワープの出力のソース座標を構築します。 |
|
画像を極座標または対数極座標空間にリマップします。 |
|
アフィン変換。 |
|
本質行列変換。 |
|
ユークリッド変換(剛体変換とも呼ばれます)。 |
|
基本行列変換。 |
|
区分アフィン変換。 |
|
2D多項式変換。 |
|
射影変換。 |
|
相似変換。 |
|
薄板スプライン変換。 |
- skimage.transform.downscale_local_mean(image, factors, cval=0, clip=True)[ソース]#
局所平均によるN次元画像のダウンサンプリング。
整数係数で完全に割り切れない場合、画像は
cvalでパディングされます。skimage.transform.resizeおよびskimage.transform.rescaleの補間とは対照的に、この関数は入力画像内のサイズfactorsの各ブロック内の要素の局所平均を計算します。- パラメータ:
- image(M[, …]) ndarray
入力画像。
- factorsarray_like
各軸に沿ったダウンサンプリング整数係数を含む配列。
- cvalfloat, optional
画像が整数係数で完全に割り切れない場合の定数パディング値。
- clipbool, optional
未使用ですが、このモジュールの他の変換とのAPIの一貫性を保つためにここに保持されています。(提供された
cvalもその範囲内に収まると仮定すると、局所平均は入力画像の値の範囲外になることはありません。)
- 戻り値:
- imagendarray
入力画像と同じ数の次元を持つダウンサンプリングされた画像。整数入力の場合、出力dtypeは
float64になります。詳細については、numpy.mean()を参照してください。
サンプル
>>> a = np.arange(15).reshape(3, 5) >>> a array([[ 0, 1, 2, 3, 4], [ 5, 6, 7, 8, 9], [10, 11, 12, 13, 14]]) >>> downscale_local_mean(a, (2, 3)) array([[3.5, 4. ], [5.5, 4.5]])
- skimage.transform.estimate_transform(ttype, src, dst, *args, **kwargs)[ソース]#
2D幾何変換パラメータを推定します。
全最小二乗法を使用して、過決定、適決定、および過小決定パラメータを決定できます。
ソース座標と宛先座標の数は一致する必要があります。
- パラメータ:
- ttype{‘euclidean’, ‘similarity’, ‘affine’, ‘piecewise-affine’, ‘projective’, ‘polynomial’}
変換の種類。
- kwargsarray_like または int
関数パラメータ(src、dst、n、angle)
NAME / TTYPE FUNCTION PARAMETERS 'euclidean' `src, `dst` 'similarity' `src, `dst` 'affine' `src, `dst` 'piecewise-affine' `src, `dst` 'projective' `src, `dst` 'polynomial' `src, `dst`, `order` (polynomial order, default order is 2)以下の例も参照してください。
- 戻り値:
- tform
_GeometricTransform 変換パラメータを含み、順変換関数と逆変換関数へのアクセスを提供する変換オブジェクト。
- tform
サンプル
>>> import numpy as np >>> import skimage as ski
>>> # estimate transformation parameters >>> src = np.array([0, 0, 10, 10]).reshape((2, 2)) >>> dst = np.array([12, 14, 1, -20]).reshape((2, 2))
>>> tform = ski.transform.estimate_transform('similarity', src, dst)
>>> np.allclose(tform.inverse(tform(src)), src) True
>>> # warp image using the estimated transformation >>> image = ski.data.camera()
>>> ski.transform.warp(image, inverse_map=tform.inverse)
>>> # create transformation with explicit parameters >>> tform2 = ski.transform.SimilarityTransform(scale=1.1, rotation=1, ... translation=(10, 20))
>>> # unite transformations, applied in order from left to right >>> tform3 = tform + tform2 >>> np.allclose(tform3(src), tform2(tform(src))) True
- skimage.transform.frt2(a)[ソース]#
入力配列の2次元有限ラドン変換(FRT)を計算します。
- パラメータ:
- a整数のndarray、形状(M、M)
入力配列。
- 戻り値:
- FRT整数のndarray、形状(M + 1、M)
有限ラドン変換の係数配列。
こちらも参照
ifrt22次元逆FRT。
注
FRTには、Mが素数の場合にのみ一意の逆があります。[FRT]このアルゴリズムのアイデアは、Vlad Negnevitskiによるものです。
参考文献
[FRT]A. Kingston and I. Svalbe, “Projective transforms on periodic discrete image arrays,” in P. Hawkes (Ed), Advances in Imaging and Electron Physics, 139 (2006)
サンプル
テスト画像を生成します。配列の次元には素数を使用します
>>> SIZE = 59 >>> img = np.tri(SIZE, dtype=np.int32)
有限ラドン変換を適用します
>>> f = frt2(img)
- skimage.transform.hough_circle(image, radius, normalize=True, full_output=False)[ソース]#
円形ハフ変換を実行します。
- パラメータ:
- imagendarray, shape (M, N)
エッジを表す非ゼロ値を持つ入力画像。
- radiusスカラーまたはスカラーのシーケンス
Hough変換を計算する半径。浮動小数点数は整数に変換されます。
- normalizeブール値, オプション
アキュムレータを、半径を描画するために使用したピクセル数で正規化します。
- full_outputブール値, オプション
入力画像の外部の中心を検出するために、出力サイズを最大の半径の2倍に拡張します。
- 戻り値:
- Hndarray, shape (半径インデックス, M + 2R, N + 2R)
各半径に対するHough変換アキュムレータ。Rは、full_outputがTrueの場合の大きな半径を表します。それ以外の場合、R = 0。
サンプル
>>> from skimage.transform import hough_circle >>> from skimage.draw import circle_perimeter >>> img = np.zeros((100, 100), dtype=bool) >>> rr, cc = circle_perimeter(25, 35, 23) >>> img[rr, cc] = 1 >>> try_radii = np.arange(5, 50) >>> res = hough_circle(img, try_radii) >>> ridx, r, c = np.unravel_index(np.argmax(res), res.shape) >>> r, c, try_radii[ridx] (25, 35, 23)
- skimage.transform.hough_circle_peaks(hspaces, radii, min_xdistance=1, min_ydistance=1, threshold=None, num_peaks=inf, total_num_peaks=inf, normalize=False)[ソース]#
円形ハフ変換のピークを返します。
与えられたHough空間で、特定の距離で分離された最も顕著な円を識別します。ピークを識別するために、Hough空間の1次元目と2次元目で異なるサイズの非最大値抑制が個別に適用されます。半径が異なり、距離が近い円の場合、最も高いピークを持つ円のみが保持されます。
- パラメータ:
- hspaces(M, N, P) 配列
hough_circle関数によって返されるHough空間。- radii(M,) 配列
Hough空間に対応する半径。
- min_xdistanceint, オプション
x次元の中心を分離する最小距離。
- min_ydistanceint, オプション
y次元の中心を分離する最小距離。
- thresholdfloat, オプション
各Hough空間におけるピークの最小強度。デフォルトは、
0.5 * max(hspace)です。- num_peaksint, オプション
各Hough空間におけるピークの最大数。ピーク数が
num_peaksを超えると、ピーク強度に基づいて、対応する半径に対してnum_peaks座標のみが考慮されます。- total_num_peaksint, オプション
ピークの最大数。ピーク数が
num_peaksを超えると、ピーク強度に基づいてnum_peaks座標を返します。- normalizebool, オプション
Trueの場合、アキュムレータを半径で正規化して、目立つピークをソートします。
- 戻り値:
- accum, cx, cy, rad配列のタプル
Hough空間におけるピーク値、xおよびy中心座標、および半径。
注
半径が大きい円は、Hough空間でより高いピークを持っています。小さな円よりも大きな円が優先される場合は、
normalizeをFalseにする必要があります。それ以外の場合、円は投票数の多い順に返されます。サンプル
>>> from skimage import transform, draw >>> img = np.zeros((120, 100), dtype=int) >>> radius, x_0, y_0 = (20, 99, 50) >>> y, x = draw.circle_perimeter(y_0, x_0, radius) >>> img[x, y] = 1 >>> hspaces = transform.hough_circle(img, radius) >>> accum, cx, cy, rad = hough_circle_peaks(hspaces, [radius,])
- skimage.transform.hough_ellipse(image, threshold=4, accuracy=1, min_size=4, max_size=None)[ソース]#
楕円ハフ変換を実行します。
- パラメータ:
- image(M, N) ndarray
エッジを表す非ゼロ値を持つ入力画像。
- thresholdint, オプション
アキュムレータの閾値。低い値を設定すると、より多くの楕円が返されます。
- accuracydouble, オプション
アキュムレータで使用される短軸のビンサイズ。値を大きくすると、より多くの楕円が返されますが、短軸長の推定精度が低下します。
- min_sizeint, オプション
長軸の最小長。
- max_sizeint, オプション
短軸の最大長。Noneの場合、値は画像の小さい方の寸法の半分に設定されます。
- 戻り値:
- resultフィールド[(accumulator, yc, xc, a, b, orientation)]を持つndarray。
(yc, xc)は中心、(a, b)はそれぞれ長軸と短軸を表します。orientationの値は、skimage.draw.ellipse_perimeterの規則に従います。
注
画像内の潜在的な楕円は、長軸長と短軸長によって特徴付けられます。画像の少なくとも
min_sizeの半分離れた2つの非ゼロピクセルのペアについて、アキュムレータは、他のすべての非ゼロピクセルで形成された潜在的な楕円の短軸長を追跡します。蓄積された短軸長のヒストグラムのいずれかのビン(bin_size = accuracy * accuracy)がthresholdを上回る場合、対応する楕円が結果に追加されます。したがって、
accuracyを大きくすると、短軸長の推定精度は低下しますが、画像内でより多くの楕円が見つかるようになります。参考文献
[1]Xie, Yonghong, and Qiang Ji. “A new efficient ellipse detection method.” Pattern Recognition, 2002. Proceedings. 16th International Conference on. Vol. 2. IEEE, 2002
サンプル
>>> from skimage.transform import hough_ellipse >>> from skimage.draw import ellipse_perimeter >>> img = np.zeros((25, 25), dtype=np.uint8) >>> rr, cc = ellipse_perimeter(10, 10, 6, 8) >>> img[cc, rr] = 1 >>> result = hough_ellipse(img, threshold=8) >>> result.tolist() [(10, 10.0, 10.0, 8.0, 6.0, 0.0)]
- skimage.transform.hough_line(image, theta=None)[ソース]#
直線ハフ変換を実行します。
- パラメータ:
- image(M, N) ndarray
エッジを表す非ゼロ値を持つ入力画像。
- thetadoubleのndarray, shape (K,), オプション
変換を計算する角度(ラジアン単位)。デフォルトでは、範囲[-pi/2, pi/2)で等間隔に配置された180個の角度のベクトルになります。
- 戻り値:
- hspaceuint64のndarray, shape (P, Q)
Hough変換アキュムレータ。
- anglesndarray
変換が計算される角度(ラジアン単位)。
- distancesndarray
距離の値。
注
原点は、元の画像の左上隅です。X軸とY軸は、それぞれ水平エッジと垂直エッジです。距離は、原点から検出された線までの最小代数距離です。
theta配列のステップサイズを小さくすることで、角度精度を向上させることができます。サンプル
テスト画像の生成
>>> img = np.zeros((100, 150), dtype=bool) >>> img[30, :] = 1 >>> img[:, 65] = 1 >>> img[35:45, 35:50] = 1 >>> for i in range(90): ... img[i, i] = 1 >>> rng = np.random.default_rng() >>> img += rng.random(img.shape) > 0.95
Hough変換の適用
>>> out, angles, d = hough_line(img)
- skimage.transform.hough_line_peaks(hspace, angles, dists, min_distance=9, min_angle=10, threshold=None, num_peaks=inf)[source]#
直線ハフ変換のピークを返します。
ハフ変換において、特定の角度と距離で区切られた最も顕著な線を識別します。ハフ空間の最初の次元(距離)と2番目の次元(角度)で、異なるサイズの非最大値抑制を別々に適用してピークを識別します。
- パラメータ:
- hspacendarray, 形状 (M, N)
hough_line関数によって返されるハフ空間。- anglesarray, 形状 (N,)
hough_line関数によって返される角度。連続していると仮定されます。(angles[-1] - angles[0] == PI)。- distsarray, 形状 (M,)
hough_line関数によって返される距離。- min_distanceint, オプション
線を区切る最小距離(ハフ空間の最初の次元の最大フィルターサイズ)。
- min_angleint, オプション
線を区切る最小角度(ハフ空間の2番目の次元の最大フィルターサイズ)。
- thresholdfloat, オプション
ピークの最小強度。デフォルトは
0.5 * max(hspace)です。- num_peaksint, オプション
ピークの最大数。ピーク数が
num_peaksを超えると、ピーク強度に基づいてnum_peaks座標を返します。
- 戻り値:
- accum, angles, dists配列のタプル
ハフ空間でのピーク値、角度、距離。
サンプル
>>> from skimage.transform import hough_line, hough_line_peaks >>> from skimage.draw import line >>> img = np.zeros((15, 15), dtype=bool) >>> rr, cc = line(0, 0, 14, 14) >>> img[rr, cc] = 1 >>> rr, cc = line(0, 14, 14, 0) >>> img[cc, rr] = 1 >>> hspace, angles, dists = hough_line(img) >>> hspace, angles, dists = hough_line_peaks(hspace, angles, dists) >>> len(angles) 2
- skimage.transform.ifrt2(a)[ソース]#
入力配列の2次元逆有限ラドン変換(iFRT)を計算します。
- パラメータ:
- aint 型の ndarray, 形状 (M+1, M)
入力配列。
- 戻り値:
- iFRTint 型の ndarray, 形状 (M, M)
逆有限ラドン変換係数。
こちらも参照
frt22次元の FRT
注
FRT は、M が素数である場合に限り、一意の逆関数を持ちます。概要については、[1] を参照してください。このアルゴリズムのアイデアは、Vlad Negnevitski によるものです。
参考文献
[1]A. Kingston and I. Svalbe, “Projective transforms on periodic discrete image arrays,” in P. Hawkes (Ed), Advances in Imaging and Electron Physics, 139 (2006)
サンプル
>>> SIZE = 59 >>> img = np.tri(SIZE, dtype=np.int32)
有限ラドン変換を適用します
>>> f = frt2(img)
逆有限ラドン変換を適用して入力を復元します。
>>> fi = ifrt2(f)
元のものと同一であることを確認してください。
>>> assert len(np.nonzero(img-fi)[0]) == 0
- skimage.transform.integral_image(image, *, dtype=None)[ソース]#
積分画像/総和領域テーブル。
積分画像には、要素の左上にあるすべての要素の合計が含まれます。つまり、
\[S[m, n] = \sum_{i \leq m} \sum_{j \leq n} X[i, j]\]- パラメータ:
- imagendarray
入力画像。
- 戻り値:
- Sndarray
入力画像と同じ形状の積分画像/累積領域テーブル。
注
精度を高め、潜在的なオーバーフローを回避するために、デフォルトの dtype が None の場合、出力のデータ型が入力のデータ型と異なる場合があります。整数 dtype の入力の場合、動作は
numpy.cumsum()の動作と一致します。浮動小数点入力は、少なくとも倍精度に昇格されます。ユーザーはdtypeを設定してこの動作を上書きできます。参考文献
[1]F.C. Crow, “テクスチャマッピングのための累積領域テーブル,” ACM SIGGRAPH Computer Graphics, vol. 18, 1984, pp. 207-212.
- skimage.transform.integrate(ii, start, end)[ソース]#
積分画像を使用して、指定されたウィンドウで積分します。
- パラメータ:
- iindarray
積分画像。
- startタプルのリスト、各タプルは
iiの次元に等しい長さ ウィンドウの左上隅の座標。リスト内の各タプルには、開始行、列、... インデックスが含まれます。つまり、
[(row_win1, col_win1, ...), (row_win2, col_win2,...), ...]。- endタプルのリスト、各タプルは
iiの次元に等しい長さ ウィンドウの右下隅の座標。リスト内の各タプルには、終了行、列、... インデックスが含まれます。つまり、
[(row_win1, col_win1, ...), (row_win2, col_win2, ...), ...]。
- 戻り値:
- Sスカラーまたはndarray
指定されたウィンドウ全体での積分(合計)。
こちらも参照
integral_image積分画像/累積領域テーブルを作成します。
サンプル
>>> arr = np.ones((5, 6), dtype=float) >>> ii = integral_image(arr) >>> integrate(ii, (1, 0), (1, 2)) # sum from (1, 0) to (1, 2) array([3.]) >>> integrate(ii, [(3, 3)], [(4, 5)]) # sum from (3, 3) to (4, 5) array([6.]) >>> # sum from (1, 0) to (1, 2) and from (3, 3) to (4, 5) >>> integrate(ii, [(1, 0), (3, 3)], [(1, 2), (4, 5)]) array([3., 6.])
- skimage.transform.iradon(radon_image, theta=None, output_size=None, filter_name='ramp', interpolation='linear', circle=True, preserve_range=True)[ソース]#
逆ラドン変換。
フィルター処理されたバックプロジェクションアルゴリズムを使用して、ラドン変換から画像を再構成します。
- パラメータ:
- radon_imagendarray
ラドン変換(サイノグラム)を含む画像。画像の各列は、異なる角度に沿った投影に対応します。トモグラフィーの回転軸は、
radon_imageの 0 次元に沿ってピクセルインデックスradon_image.shape[0] // 2にある必要があります。- thetaarray, オプション
再構成角度(度単位)。デフォルト:0から180の間に均等に配置されたm個の角度(
radon_imageの形状が (N, M) の場合)。- output_sizeint, オプション
再構成における行と列の数。
- filter_namestr, オプション
周波数領域フィルタリングで使用されるフィルター。デフォルトで使用されるランプフィルター。利用可能なフィルター:ramp、shepp-logan、cosine、hamming、hann。フィルターを使用しない場合は None を割り当てます。
- interpolationstr, オプション
再構成で使用される補間方法。利用可能な方法:'linear'、'nearest'、および 'cubic' ('cubic' は遅いです)。
- circleboolean, オプション
再構成された画像は内接円の外側でゼロであると仮定します。また、
circle=Trueで呼び出されたradonの動作に一致するように、デフォルトの output_size も変更します。- preserve_rangebool, オプション
元の値の範囲を保持するかどうか。それ以外の場合、入力画像は
img_as_floatの規則に従って変換されます。 https://scikit-image.dokyumento.jp/docs/dev/user_guide/data_types.html も参照してください。
- 戻り値:
- reconstructedndarray
再構成された画像。回転軸は、インデックスが
(reconstructed.shape[0] // 2, reconstructed.shape[1] // 2)のピクセルに配置されます。
バージョン 0.19 で変更:
iradonでは、filter引数がfilter_nameに代わって非推奨になりました。
注
フーリエスライス定理を適用して、フィルターの周波数領域と投影データの FFT を乗算することにより、画像を再構成します。このアルゴリズムは、フィルター処理されたバックプロジェクションと呼ばれます。
参考文献
[1]AC Kak, M Slaney, “コンピュータ化された断層撮影イメージングの原理”, IEEE Press 1988.
[2]B.R. Ramesh, N. Srinivasa, K. Rajgopal, “いくつかのアプリケーションを使用した離散ラドン変換を計算するアルゴリズム”, 第 4 回 IEEE リージョン 10 国際会議議事録、TENCON ‘89, 1989
- skimage.transform.iradon_sart(radon_image, theta=None, image=None, projection_shifts=None, clip=None, relaxation=0.15, dtype=None)[ソース]#
逆ラドン変換。
Simultaneous Algebraic Reconstruction Technique (SART)アルゴリズムの単一の反復を使用して、ラドン変換から画像を再構築します。
- パラメータ:
- radon_imagendarray, 形状 (M, N)
ラドン変換(サイノグラム)を含む画像。画像の各列は、異なる角度に沿った投影に対応します。トモグラフィーの回転軸は、
radon_imageの 0 次元に沿ってピクセルインデックスradon_image.shape[0] // 2にある必要があります。- thetaarray, 形状 (N,), オプション
再構成角度(度単位)。デフォルト:0から180の間に均等に配置されたm個の角度(
radon_imageの形状が (N, M) の場合)。- imagendarray, 形状 (M, M), オプション
初期再構成推定値を含む画像。デフォルトはゼロの配列です。
- projection_shiftsarray, 形状 (N,), オプション
画像を再構成する前に、
radon_image(サイノグラム) に含まれる投影をこのピクセル数だけシフトします。i番目の値は、radon_imageのi番目の列のシフトを定義します。- clip長さ2のfloatのシーケンス、オプション
再構成されたトモグラム内のすべての値を範囲
[clip[0], clip[1]]に強制します。- relaxationfloat, オプション
更新ステップのリラクゼーションパラメータ。値を大きくすると収束率が向上する可能性がありますが、不安定になるリスクがあります。1に近い値または1より大きい値は推奨されません。
- dtypedtype, オプション
出力データ型。浮動小数点数である必要があります。デフォルトでは、入力データ型がfloatでない場合は、入力はdoubleにキャストされ、それ以外の場合はdtypeが入力データ型に設定されます。
- 戻り値:
- reconstructedndarray
再構成された画像。回転軸は、インデックスが
(reconstructed.shape[0] // 2, reconstructed.shape[1] // 2)のピクセルに配置されます。
注
代数再構成技術は、トモグラフィー再構成問題を一連の線形方程式として定式化することに基づいています。各光線に沿って、投影された値は光線に沿った断面のすべての値の合計です。SART(およびいくつかの他の代数技術のバリアント)の典型的な特徴は、断面のピクセル値間の線形補間を使用して、光線に沿って等距離の点で断面をサンプリングすることです。得られた一連の線形方程式は、わずかに変更されたKaczmarz法を使用して解かれます。
SARTを使用する場合、通常、良好な再構成を得るには1回の反復で十分です。さらに反復すると、高周波情報が強調される傾向がありますが、ノイズも増加することがよくあります。
参考文献
[1]AC Kak, M Slaney, “コンピュータ化された断層撮影イメージングの原理”, IEEE Press 1988.
[2]AH Andersen, AC Kak, “Simultaneous algebraic reconstruction technique (SART): a superior implementation of the ART algorithm”, Ultrasonic Imaging 6 pp 81–94 (1984)
[3]S Kaczmarz, “Angenäherte auflösung von systemen linearer gleichungen”, Bulletin International de l’Academie Polonaise des Sciences et des Lettres 35 pp 355–357 (1937)
[4]Kohler, T. “A projection access scheme for iterative reconstruction based on the golden section.” Nuclear Science Symposium Conference Record, 2004 IEEE. Vol. 6. IEEE, 2004.
[5]Kaczmarz’ method, Wikipedia, https://en.wikipedia.org/wiki/Kaczmarz_method
- skimage.transform.matrix_transform(coords, matrix)[ソース]#
2Dマトリックス変換を適用します。
- パラメータ:
- coords(N, 2) array_like
変換するx, y座標
- matrix(3, 3) array_like
同次変換行列。
- 戻り値:
- coords(N, 2) array
変換された座標。
- skimage.transform.order_angles_golden_ratio(theta)[ソース]#
後続の投影における相関情報の量を減らすために角度を順序付けます。
- パラメータ:
- thetafloatの配列, 形状 (M,)
度単位の投影角度。重複する角度は許可されていません。
- 戻り値:
- indices_generator符号なし整数を生成するジェネレーター
返されるジェネレーターは、
theta[indices]が投影の近似的な黄金比順序を与えるようなthetaへのインデックスを生成します。合計で、len(theta)個のインデックスが生成されます。すべての非負整数 <len(theta)は正確に1回生成されます。
注
ここで使用される方法は、T. Kohlerが導入した黄金比の方法です。
参考文献
[1]Kohler, T. “A projection access scheme for iterative reconstruction based on the golden section.” Nuclear Science Symposium Conference Record, 2004 IEEE. Vol. 6. IEEE, 2004.
[2]Winkelmann, Stefanie, et al. “An optimal radial profile order based on the Golden Ratio for time-resolved MRI.” Medical Imaging, IEEE Transactions on 26.1 (2007): 68-76.
- skimage.transform.probabilistic_hough_line(image, threshold=10, line_length=50, line_gap=10, theta=None, rng=None)[ソース]#
進行的な確率的線ハフ変換から線を返します。
- パラメータ:
- imagendarray, shape (M, N)
エッジを表す非ゼロ値を持つ入力画像。
- thresholdint, オプション
閾値
- line_lengthint, オプション
検出された線の最小許容長さ。より長い線を抽出するには、パラメータを大きくしてください。
- line_gapint, オプション
線を形成するためのピクセル間の最大ギャップ。壊れた線をより積極的にマージするには、パラメータを大きくしてください。
- thetadtypeのndarray, 形状 (K,), オプション
変換を計算する角度(ラジアン単位)。デフォルトでは、範囲[-pi/2, pi/2)で等間隔に配置された180個の角度のベクトルになります。
- rng{
numpy.random.Generator, int}, オプション 疑似乱数ジェネレーター。デフォルトでは、PCG64ジェネレーターが使用されます(
numpy.random.default_rng()を参照)。rngがintの場合、ジェネレーターのシードに使用されます。
- 戻り値:
- lineslist
識別された線のリスト。線は ((x0, y0), (x1, y1)) の形式で、線の開始と終了を示します。
参考文献
[1]C. Galamhos, J. Matas and J. Kittler, “Progressive probabilistic Hough transform for line detection”, in IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 1999.
- skimage.transform.pyramid_expand(image, upscale=2, sigma=None, order=1, mode='reflect', cval=0, preserve_range=False, *, channel_axis=None)[ソース]#
画像をアップサンプリングしてから平滑化します。
- パラメータ:
- imagendarray
入力画像。
- upscalefloat, オプション
アップスケール係数。
- sigmafloat, オプション
ガウシアンフィルターのシグマ。デフォルトは
2 * upscale / 6.0であり、これはガウス分布の99%以上をカバーするスケールファクターの2倍のサイズのフィルターマスクに対応します。- orderint, オプション
アップサンプリングの補間に使用されるスプラインの次数。詳細については、
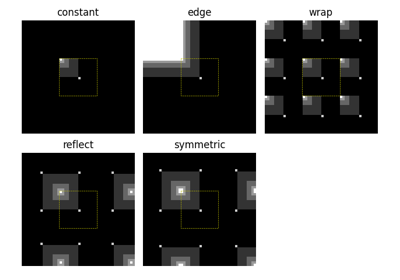
skimage.transform.warpを参照してください。- mode{‘reflect’, ‘constant’, ‘edge’, ‘symmetric’, ‘wrap’}, オプション
mode パラメーターは、配列の境界をどのように処理するかを決定します。ここで、cval は mode が ‘constant’ の場合の値を表します。
- cvalfloat, optional
mode が ‘constant’ の場合、入力の端を超えた領域を埋める値です。
- preserve_rangebool, オプション
元の値の範囲を保持するかどうか。それ以外の場合、入力画像は
img_as_floatの規則に従って変換されます。 https://scikit-image.dokyumento.jp/docs/dev/user_guide/data_types.html も参照してください。- channel_axisint または None, optional
None の場合、画像はグレースケール(シングルチャンネル)画像とみなされます。それ以外の場合、このパラメーターは配列のどの軸がチャンネルに対応するかを示します。
バージョン 0.19 で追加:
channel_axisが 0.19 で追加されました。
- 戻り値:
- outarray
アップサンプルおよび平滑化された float 画像。
参考文献
- skimage.transform.pyramid_gaussian(image, max_layer=-1, downscale=2, sigma=None, order=1, mode='reflect', cval=0, preserve_range=False, *, channel_axis=None)[source]#
入力画像によって形成されたガウスピラミッドの画像を生成します。
画像に対して
pyramid_reduce関数を再帰的に適用し、ダウンサンプリングされた画像を生成します。ピラミッドの最初の画像は、元のスケーリングされていない画像であることに注意してください。画像の総数は
max_layer + 1です。すべてのレイヤーが計算される場合、最後の画像は1ピクセル画像であるか、縮小によって形状が変わらない画像です。- パラメータ:
- imagendarray
入力画像。
- max_layerint, optional
ピラミッドのレイヤー数。0番目のレイヤーは元の画像です。デフォルトは-1で、可能なすべてのレイヤーを構築します。
- downscalefloat, optional
ダウン スケール ファクター。
- sigmafloat, オプション
ガウシアンフィルターのシグマ。デフォルトは
2 * downscale / 6.0で、これはスケールファクターの2倍のサイズのフィルターマスクに対応し、ガウス分布の99%以上をカバーします。- orderint, オプション
ダウンサンプリングの補間に使用されるスプラインの次数。詳細については、
skimage.transform.warpを参照してください。- mode{‘reflect’, ‘constant’, ‘edge’, ‘symmetric’, ‘wrap’}, オプション
mode パラメーターは、配列の境界をどのように処理するかを決定します。ここで、cval は mode が ‘constant’ の場合の値を表します。
- cvalfloat, optional
mode が ‘constant’ の場合、入力の端を超えた領域を埋める値です。
- preserve_rangebool, オプション
元の値の範囲を保持するかどうか。それ以外の場合、入力画像は
img_as_floatの規則に従って変換されます。 https://scikit-image.dokyumento.jp/docs/dev/user_guide/data_types.html も参照してください。- channel_axisint または None, optional
None の場合、画像はグレースケール(シングルチャンネル)画像とみなされます。それ以外の場合、このパラメーターは配列のどの軸がチャンネルに対応するかを示します。
バージョン 0.19 で追加:
channel_axisが 0.19 で追加されました。
- 戻り値:
- pyramidgenerator
ピラミッドレイヤーをfloat画像として生成するジェネレーター。
参考文献
- skimage.transform.pyramid_laplacian(image, max_layer=-1, downscale=2, sigma=None, order=1, mode='reflect', cval=0, preserve_range=False, *, channel_axis=None)[source]#
入力画像によって形成されたラプラシアンピラミッドの画像を生成します。
各レイヤーには、ダウンサンプリングされた画像と、ダウンサンプリングおよび平滑化された画像の差が含まれています。
layer = resize(prev_layer) - smooth(resize(prev_layer))
ピラミッドの最初の画像は、元のスケーリングされていない画像とその平滑化バージョンの差であることに注意してください。画像の総数は
max_layer + 1です。すべてのレイヤーが計算される場合、最後の画像は1ピクセル画像であるか、縮小によって形状が変わらない画像です。- パラメータ:
- imagendarray
入力画像。
- max_layerint, optional
ピラミッドのレイヤー数。0番目のレイヤーは元の画像です。デフォルトは-1で、可能なすべてのレイヤーを構築します。
- downscalefloat, optional
ダウン スケール ファクター。
- sigmafloat, オプション
ガウシアンフィルターのシグマ。デフォルトは
2 * downscale / 6.0で、これはスケールファクターの2倍のサイズのフィルターマスクに対応し、ガウス分布の99%以上をカバーします。- orderint, オプション
ダウンサンプリングの補間に使用されるスプラインの次数。詳細については、
skimage.transform.warpを参照してください。- mode{‘reflect’, ‘constant’, ‘edge’, ‘symmetric’, ‘wrap’}, オプション
mode パラメーターは、配列の境界をどのように処理するかを決定します。ここで、cval は mode が ‘constant’ の場合の値を表します。
- cvalfloat, optional
mode が ‘constant’ の場合、入力の端を超えた領域を埋める値です。
- preserve_rangebool, オプション
元の値の範囲を保持するかどうか。それ以外の場合、入力画像は
img_as_floatの規則に従って変換されます。 https://scikit-image.dokyumento.jp/docs/dev/user_guide/data_types.html も参照してください。- channel_axisint または None, optional
None の場合、画像はグレースケール(シングルチャンネル)画像とみなされます。それ以外の場合、このパラメーターは配列のどの軸がチャンネルに対応するかを示します。
バージョン 0.19 で追加:
channel_axisが 0.19 で追加されました。
- 戻り値:
- pyramidgenerator
ピラミッドレイヤーをfloat画像として生成するジェネレーター。
参考文献
- skimage.transform.pyramid_reduce(image, downscale=2, sigma=None, order=1, mode='reflect', cval=0, preserve_range=False, *, channel_axis=None)[source]#
画像を平滑化してからダウンサンプリングします。
- パラメータ:
- imagendarray
入力画像。
- downscalefloat, optional
ダウン スケール ファクター。
- sigmafloat, オプション
ガウシアンフィルターのシグマ。デフォルトは
2 * downscale / 6.0で、これはスケールファクターの2倍のサイズのフィルターマスクに対応し、ガウス分布の99%以上をカバーします。- orderint, オプション
ダウンサンプリングの補間に使用されるスプラインの次数。詳細については、
skimage.transform.warpを参照してください。- mode{‘reflect’, ‘constant’, ‘edge’, ‘symmetric’, ‘wrap’}, オプション
mode パラメーターは、配列の境界をどのように処理するかを決定します。ここで、cval は mode が ‘constant’ の場合の値を表します。
- cvalfloat, optional
mode が ‘constant’ の場合、入力の端を超えた領域を埋める値です。
- preserve_rangebool, オプション
元の値の範囲を保持するかどうか。それ以外の場合、入力画像は
img_as_floatの規則に従って変換されます。 https://scikit-image.dokyumento.jp/docs/dev/user_guide/data_types.html も参照してください。- channel_axisint または None, optional
None の場合、画像はグレースケール(シングルチャンネル)画像とみなされます。それ以外の場合、このパラメーターは配列のどの軸がチャンネルに対応するかを示します。
バージョン 0.19 で追加:
channel_axisが 0.19 で追加されました。
- 戻り値:
- outarray
平滑化およびダウンサンプリングされた float 画像。
参考文献
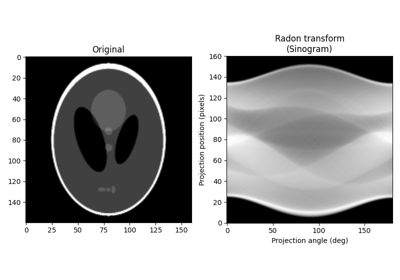
- skimage.transform.radon(image, theta=None, circle=True, *, preserve_range=False)[source]#
指定された投影角度で画像のラドン変換を計算します。
- パラメータ:
- imagendarray
入力画像。回転軸は、インデックス
(image.shape[0] // 2, image.shape[1] // 2)を持つピクセルに配置されます。- thetaarray, オプション
投影角度(度単位)。
Noneの場合、値は np.arange(180) に設定されます。- circleboolean, オプション
画像は内接円の外側ではゼロであると仮定し、各投影の幅(シノグラムの最初の次元)を
min(image.shape)と等しくします。- preserve_rangebool, オプション
元の値の範囲を保持するかどうか。それ以外の場合、入力画像は
img_as_floatの規則に従って変換されます。 https://scikit-image.dokyumento.jp/docs/dev/user_guide/data_types.html も参照してください。
- 戻り値:
- radon_imagendarray
ラドン変換(シノグラム)。トモグラフィーの回転軸は、
radon_imageの0番目の次元に沿って、ピクセルインデックスradon_image.shape[0] // 2に位置します。
注
Justin K. Romberg のコードに基づいています (https://www.clear.rice.edu/elec431/projects96/DSP/bpanalysis.html)
参考文献
[1]AC Kak, M Slaney, “コンピュータ化された断層撮影イメージングの原理”, IEEE Press 1988.
[2]B.R. Ramesh, N. Srinivasa, K. Rajgopal, “いくつかのアプリケーションを使用した離散ラドン変換を計算するアルゴリズム”, 第 4 回 IEEE リージョン 10 国際会議議事録、TENCON ‘89, 1989
- skimage.transform.rescale(image, scale, order=None, mode='reflect', cval=0, clip=True, preserve_range=False, anti_aliasing=None, anti_aliasing_sigma=None, *, channel_axis=None)[source]#
画像を特定の係数でスケーリングします。
N次元画像のアップスケールまたはダウンスケールを行うために補間を実行します。エイリアシングアーティファクトを避けるために、画像をダウンサイズする際にはアンチエイリアシングを有効にする必要があることに注意してください。整数係数でのダウンサンプリングについては、
skimage.transform.downscale_local_meanも参照してください。- パラメータ:
- image(M, N[, …][, C]) ndarray
入力画像。
- scale{float, floatのタプル}
空間次元のスケーリング係数。個別のスケーリング係数を(m, n[, …])として定義できます。
- 戻り値:
- scaledndarray
入力のスケーリングされたバージョン。
- その他のパラメータ:
- orderint, オプション
スプライン補間の次数。デフォルトは、image.dtypeがboolの場合は0、それ以外の場合は1です。次数は0〜5の範囲でなければなりません。詳細については、
skimage.transform.warpを参照してください。- mode{‘constant’, ‘edge’, ‘symmetric’, ‘reflect’, ‘wrap’}, オプション
入力の境界外の点は、指定されたモードに従って塗りつぶされます。モードは、
numpy.padの動作に一致します。- cvalfloat, optional
モード ‘constant’ と組み合わせて使用される場合、画像境界外の値です。
- clipbool, optional
出力を入力画像の範囲の値にクリップするかどうか。高次補間によって指定された入力範囲外の値が生成される可能性があるため、デフォルトで有効になっています。
- preserve_rangebool, オプション
元の値の範囲を保持するかどうか。それ以外の場合、入力画像は
img_as_floatの規則に従って変換されます。 https://scikit-image.dokyumento.jp/docs/dev/user_guide/data_types.html も参照してください。- anti_aliasingbool, オプション
ダウンスケーリングする前に、ガウシアンフィルターを適用して画像を平滑化するかどうか。エイリアシングアーティファクトを避けるために、画像をダウンサンプリングする際にはフィルタリングが重要です。入力画像データ型がboolの場合、アンチエイリアシングは適用されません。
- anti_aliasing_sigma{float, floatのタプル}, オプション
エイリアシングアーティファクトを避けるためのガウシアンフィルタリングの標準偏差。デフォルトでは、この値はダウンサンプリング係数sに対して(s - 1) / 2として選択されます。
- channel_axisint または None, optional
None の場合、画像はグレースケール(シングルチャンネル)画像とみなされます。それ以外の場合、このパラメーターは配列のどの軸がチャンネルに対応するかを示します。
バージョン 0.19 で追加:
channel_axisが 0.19 で追加されました。
注
モード ‘reflect’ と ‘symmetric’ は似ていますが、反射中にエッジピクセルが複製されるかどうかで異なります。たとえば、配列の値が [0, 1, 2] で、symmetric を使用して右側に4つの値がパディングされた場合、結果は [0, 1, 2, 2, 1, 0, 0] になります。一方、reflect の場合は [0, 1, 2, 1, 0, 1, 2] になります。
サンプル
>>> from skimage import data >>> from skimage.transform import rescale >>> image = data.camera() >>> rescale(image, 0.1).shape (51, 51) >>> rescale(image, 0.5).shape (256, 256)
- skimage.transform.resize(image, output_shape, order=None, mode='reflect', cval=0, clip=True, preserve_range=False, anti_aliasing=None, anti_aliasing_sigma=None)[source]#
画像を特定のサイズにリサイズします。
N次元画像のアップサイズまたはダウンサイズを行うために補間を実行します。エイリアシングアーティファクトを避けるために、画像をダウンサイズする際にはアンチエイリアシングを有効にする必要があることに注意してください。整数係数でのダウンサンプリングについては、
skimage.transform.downscale_local_meanも参照してください。- パラメータ:
- imagendarray
入力画像。
- output_shapeiterable
生成される出力画像のサイズ
(rows, cols[, ...][, dim])。dimが指定されていない場合、チャネル数が保持されます。入力チャネル数が出力チャネル数と等しくない場合、n次元補間が適用されます。
- 戻り値:
- resizedndarray
入力のリサイズされたバージョン。
- その他のパラメータ:
- orderint, オプション
スプライン補間の次数。デフォルトは、image.dtypeがboolの場合は0、それ以外の場合は1です。次数は0〜5の範囲でなければなりません。詳細については、
skimage.transform.warpを参照してください。- mode{‘constant’, ‘edge’, ‘symmetric’, ‘reflect’, ‘wrap’}, オプション
入力の境界外の点は、指定されたモードに従って塗りつぶされます。モードは、
numpy.padの動作に一致します。- cvalfloat, optional
モード ‘constant’ と組み合わせて使用される場合、画像境界外の値です。
- clipbool, optional
出力を入力画像の範囲の値にクリップするかどうか。高次補間によって指定された入力範囲外の値が生成される可能性があるため、デフォルトで有効になっています。
- preserve_rangebool, オプション
元の値の範囲を保持するかどうか。それ以外の場合、入力画像は
img_as_floatの規則に従って変換されます。 https://scikit-image.dokyumento.jp/docs/dev/user_guide/data_types.html も参照してください。- anti_aliasingbool, オプション
ダウンサンプリングする前に、ガウシアンフィルターを適用して画像を平滑化するかどうか。エイリアシングアーティファクトを避けるために、画像をダウンサンプリングする際にはフィルタリングが重要です。指定しない場合、データ型がboolではない画像をダウンサンプリングするときはTrueに設定されます。また、整数入力データ型で最近傍補間(
order== 0)を使用する場合はFalseに設定されます。- anti_aliasing_sigma{float, floatのタプル}, オプション
アンチエイリアシング時に使用されるガウシアンフィルタリングの標準偏差。デフォルトでは、この値はダウンサンプリング係数sに対して(s - 1) / 2として選択されます。ここで、s > 1です。アップサイズの場合、s < 1では、リサイジングの前にアンチエイリアシングは実行されません。
注
モード ‘reflect’ と ‘symmetric’ は似ていますが、反射中にエッジピクセルが複製されるかどうかで異なります。たとえば、配列の値が [0, 1, 2] で、symmetric を使用して右側に4つの値がパディングされた場合、結果は [0, 1, 2, 2, 1, 0, 0] になります。一方、reflect の場合は [0, 1, 2, 1, 0, 1, 2] になります。
サンプル
>>> from skimage import data >>> from skimage.transform import resize >>> image = data.camera() >>> resize(image, (100, 100)).shape (100, 100)
- skimage.transform.resize_local_mean(image, output_shape, grid_mode=True, preserve_range=False, *, channel_axis=None)[source]#
局所平均/双一次スケーリングで配列をリサイズします。
- パラメータ:
- imagendarray
入力画像。これがマルチチャネル画像の場合、
channel_axisを使用してチャネルに対応する軸を指定する必要があります。- output_shapeiterable
生成される出力画像のサイズ。
channel_axisがNoneでない場合、channel_axisはoutput_shapeから省略するか、output_shape[channel_axis]はimage.shape[channel_axis]と一致する必要があります。output_shapeの長さが image.ndim を超える場合、必要に応じて、追加のシングルトン次元が入力imageに追加されます。- grid_modebool, オプション
imageピクセルの位置を定義します。Trueの場合、ピクセルはグリッド交点にあるとみなされ、それ以外の場合はセル中心にあるとみなされます。その結果、たとえば、長さ5の1次元信号は、grid_modeがFalseの場合は長さ4とみなされますが、grid_modeがTrueの場合は長さ5とみなされます。以下の図解を参照してください。| pixel 1 | pixel 2 | pixel 3 | pixel 4 | pixel 5 | |<-------------------------------------->| vs. |<----------------------------------------------->|上記の図の矢印の始点は、各モードの座標位置0に対応します。
- preserve_rangebool, オプション
元の値の範囲を保持するかどうか。それ以外の場合、入力画像は
img_as_floatの規則に従って変換されます。 https://scikit-image.dokyumento.jp/docs/dev/user_guide/data_types.html も参照してください。
- 戻り値:
- resizedndarray
入力のリサイズされたバージョン。
こちらも参照
注
この方法は、「面積ベース」補間または「ピクセルミキシング」補間とも呼ばれることがあります[1]。
grid_modeがTrueの場合、OpenCVのリサイズをINTER_AREA補間モードで使用するのと同等です。これは、一般に画像のダウンサイジングに使用されます。ダウンサイジング係数が整数の場合、代わりにdownscale_local_meanを使用する必要があります。参考文献
サンプル
>>> from skimage import data >>> from skimage.transform import resize_local_mean >>> image = data.camera() >>> resize_local_mean(image, (100, 100)).shape (100, 100)
- skimage.transform.rotate(image, angle, resize=False, center=None, order=None, mode='constant', cval=0, clip=True, preserve_range=False)[ソース]#
画像の中心を基準にして、画像を特定の角度で回転させます。
- パラメータ:
- imagendarray
入力画像。
- anglefloat
反時計回りの回転角度(度単位)。
- resizebool, optional
回転後の画像全体がぴったり収まるように、出力画像の形状を自動的に計算するかどうかを決定します。デフォルトはFalseです。
- center長さ2のイテラブル
回転の中心。
center=Noneの場合、画像はその中心、つまりcenter=(cols / 2 - 0.5, rows / 2 - 0.5)を中心に回転します。このパラメーターは、通常のskimageの順序とは異なり、(cols, rows)であることに注意してください。
- 戻り値:
- rotatedndarray
入力の回転版。
- その他のパラメータ:
- orderint, オプション
スプライン補間の次数。デフォルトは、image.dtypeがboolの場合は0、それ以外の場合は1です。次数は0〜5の範囲でなければなりません。詳細については、
skimage.transform.warpを参照してください。- mode{‘constant’, ‘edge’, ‘symmetric’, ‘reflect’, ‘wrap’}, オプション
入力の境界外の点は、指定されたモードに従って塗りつぶされます。モードは、
numpy.padの動作に一致します。- cvalfloat, optional
モード ‘constant’ と組み合わせて使用される場合、画像境界外の値です。
- clipbool, optional
出力を入力画像の範囲の値にクリップするかどうか。高次補間によって指定された入力範囲外の値が生成される可能性があるため、デフォルトで有効になっています。
- preserve_rangebool, オプション
元の値の範囲を保持するかどうか。それ以外の場合、入力画像は
img_as_floatの規則に従って変換されます。 https://scikit-image.dokyumento.jp/docs/dev/user_guide/data_types.html も参照してください。
注
モード ‘reflect’ と ‘symmetric’ は似ていますが、反射中にエッジピクセルが複製されるかどうかで異なります。たとえば、配列の値が [0, 1, 2] で、symmetric を使用して右側に4つの値がパディングされた場合、結果は [0, 1, 2, 2, 1, 0, 0] になります。一方、reflect の場合は [0, 1, 2, 1, 0, 1, 2] になります。
サンプル
>>> from skimage import data >>> from skimage.transform import rotate >>> image = data.camera() >>> rotate(image, 2).shape (512, 512) >>> rotate(image, 2, resize=True).shape (530, 530) >>> rotate(image, 90, resize=True).shape (512, 512)
- skimage.transform.swirl(image, center=None, strength=1, radius=100, rotation=0, output_shape=None, order=None, mode='reflect', cval=0, clip=True, preserve_range=False)[ソース]#
渦巻き変換を実行します。
- パラメータ:
- imagendarray
入力画像。
- center(column, row)タプルまたは(2,) ndarray, optional
変換の中心座標。
- strengthfloat, optional
適用される渦巻きの量。
- radiusfloat, optional
渦巻きの範囲(ピクセル単位)。効果は、
radiusを超えると急速に薄れます。- rotationfloat, optional
画像に適用される追加の回転。
- 戻り値:
- swirledndarray
入力の渦巻き版。
- その他のパラメータ:
- output_shapetuple (rows, cols), optional
生成される出力画像の形状。デフォルトでは、入力画像の形状が保持されます。
- orderint, オプション
スプライン補間の次数。デフォルトは、image.dtypeがboolの場合は0、それ以外の場合は1です。次数は0〜5の範囲でなければなりません。詳細については、
skimage.transform.warpを参照してください。- mode{‘constant’, ‘edge’, ‘symmetric’, ‘reflect’, ‘wrap’}, オプション
入力の境界外の点は、指定されたモードに従って塗りつぶされ、デフォルトとして「reflect」が使用されます。モードは、
numpy.padの動作と一致します。- cvalfloat, optional
モード ‘constant’ と組み合わせて使用される場合、画像境界外の値です。
- clipbool, optional
出力を入力画像の範囲の値にクリップするかどうか。高次補間によって指定された入力範囲外の値が生成される可能性があるため、デフォルトで有効になっています。
- preserve_rangebool, オプション
元の値の範囲を保持するかどうか。それ以外の場合、入力画像は
img_as_floatの規則に従って変換されます。 https://scikit-image.dokyumento.jp/docs/dev/user_guide/data_types.html も参照してください。
- skimage.transform.warp(image, inverse_map, map_args=None, output_shape=None, order=None, mode='constant', cval=0.0, clip=True, preserve_range=False)[ソース]#
指定された座標変換に従って画像をワープします。
- パラメータ:
- imagendarray
入力画像。
- inverse_map変換オブジェクト, 呼び出し可能
cr = f(cr, **kwargs), またはndarray 出力画像内の座標を、入力画像内の対応する座標に変換する逆座標マップ。
入力画像の次元に応じて、このマップを定義するためのさまざまなオプションがあります。2次元画像は、グレースケール画像の場合は2次元、カラー情報を含む場合は3次元を持つことができます。
2次元画像の場合、
skimage.transform.SimilarityTransformなどの変換オブジェクト、またはその逆を直接渡すことができます。2次元画像の場合、
(3, 3)の同次変換行列、たとえばskimage.transform.SimilarityTransform.paramsを渡すことができます。2次元画像の場合、出力画像の
(col, row)座標の(M, 2)配列を、入力画像の対応する座標に変換する関数。関数の追加パラメーターは、map_argsで指定できます。N次元画像の場合、座標の配列を直接渡すことができます。最初の次元は入力画像の座標を指定し、後続の次元は出力画像の位置を決定します。例えば、2次元画像の場合、
(2, rows, cols)の形状の配列を渡す必要があります。ここで、rowsとcolsは出力画像の形状を決定し、最初の次元には入力画像の(row, col)座標が含まれています。詳細については、scipy.ndimage.map_coordinatesを参照してください。
(3, 3)行列は同次変換行列として解釈されるため、出力が(3,)の形状の場合、3次元入力から値を補間することはできません。使用例については、例のセクションを参照してください。
- map_argsdict, optional
inverse_mapに渡されるキーワード引数。- output_shapetuple (rows, cols), optional
生成される出力画像の形状。デフォルトでは、入力画像の形状が保持されます。マルチバンド画像の場合でも、指定する必要があるのは行と列のみであることに注意してください。
- orderint, オプション
- 補間の次数。次数は0〜5の範囲でなければなりません
0:最近傍
1:双一次(デフォルト)
2:双二次
3:双三次
4:双四次
5:双五次
image.dtypeがboolの場合は0、それ以外の場合は1がデフォルトです。
- mode{‘constant’, ‘edge’, ‘symmetric’, ‘reflect’, ‘wrap’}, オプション
入力の境界外の点は、指定されたモードに従って塗りつぶされます。モードは、
numpy.padの動作に一致します。- cvalfloat, optional
モード ‘constant’ と組み合わせて使用される場合、画像境界外の値です。
- clipbool, optional
出力を入力画像の範囲の値にクリップするかどうか。高次補間によって指定された入力範囲外の値が生成される可能性があるため、デフォルトで有効になっています。
- preserve_rangebool, オプション
元の値の範囲を保持するかどうか。それ以外の場合、入力画像は
img_as_floatの規則に従って変換されます。 https://scikit-image.dokyumento.jp/docs/dev/user_guide/data_types.html も参照してください。
- 戻り値:
- warpeddouble ndarray
ワープされた入力画像。
注
入力画像は
double画像に変換されます。SimilarityTransform、AffineTransform、ProjectiveTransformの場合、およびorderが[0, 3]の場合、この関数は、はるかに高速なルーチンで画像をワープするために、基礎となる変換行列を使用します。
サンプル
>>> from skimage.transform import warp >>> from skimage import data >>> image = data.camera()
以下の画像のワープはすべて同じですが、実行時間に大幅な違いがあります。画像は下にシフトします。
幾何変換を使用して画像をワープする(高速)
>>> from skimage.transform import SimilarityTransform >>> tform = SimilarityTransform(translation=(0, -10)) >>> warped = warp(image, tform)
呼び出し可能オブジェクトを使用する(低速)
>>> def shift_down(xy): ... xy[:, 1] -= 10 ... return xy >>> warped = warp(image, shift_down)
変換行列を使用して画像をワープする(高速)
>>> matrix = np.array([[1, 0, 0], [0, 1, -10], [0, 0, 1]]) >>> warped = warp(image, matrix) >>> from skimage.transform import ProjectiveTransform >>> warped = warp(image, ProjectiveTransform(matrix=matrix))
幾何変換の逆を使用することもできます(高速)
>>> warped = warp(image, tform.inverse)
N次元画像の場合、出力画像のすべての要素の入力画像内の座標を指定する座標配列を渡すことができます。例えば、3次元の立方体をリスケールしたい場合は、次のようにします。
>>> cube_shape = np.array([30, 30, 30]) >>> rng = np.random.default_rng() >>> cube = rng.random(cube_shape)
スケーリングを定義する座標配列を設定します
>>> scale = 0.1 >>> output_shape = (scale * cube_shape).astype(int) >>> coords0, coords1, coords2 = np.mgrid[:output_shape[0], ... :output_shape[1], :output_shape[2]] >>> coords = np.array([coords0, coords1, coords2])
立方体には空間データが含まれており、最初の配列要素の中心が実空間の座標(0.5, 0.5, 0.5)にあると仮定します。つまり、画像をスケーリングするときにこの追加オフセットを考慮する必要があります
>>> coords = (coords + 0.5) / scale - 0.5 >>> warped = warp(cube, coords)
- skimage.transform.warp_coords(coord_map, shape, dtype=<class 'numpy.float64'>)[source]#
2D画像ワープの出力のソース座標を構築します。
- パラメータ:
- coord_mapGeometricTransform.inverse のような callable
指定された出力座標に対する入力座標を返します。座標は (P, 2) の形状で、P は座標の数で、各要素は
(行, 列)のペアです。- shapetuple
出力画像の形状
(行数, 列数[, バンド数])。- dtypenp.dtype または文字列
戻り値の dtype (適切な選択肢: float32 または float64)。
- 戻り値:
- coords(ndim, 行数, 列数[, バンド数]) dtype
dtypeの配列 scipy.ndimage.map_coordinates のための座標で、
coord_transform_fnに従ってソースポイントから描画することにより、(orows, ocols, バンド数) の形状の画像を生成します。
- coords(ndim, 行数, 列数[, バンド数]) dtype
注
これは、
warp()で使用される2次元画像のソース座標を生成する低レベルルーチンです。これは、例えば、特定の座標マッピングを再利用したり、画像ワーピングプロセスの様々なポイントで特定のdtypeを使用したり、
ndi.map_coordinatesの呼び出し後にwarpが実行するロジックとは異なる後処理ロジックを実装したりする場合に、ユーザーに追加の柔軟性を提供するために、warpとは別に提供されます。サンプル
画像を上と右にシフトする座標マップを生成します
>>> from skimage import data >>> from scipy.ndimage import map_coordinates >>> >>> def shift_up10_left20(xy): ... return xy - np.array([-20, 10])[None, :] >>> >>> image = data.astronaut().astype(np.float32) >>> coords = warp_coords(shift_up10_left20, image.shape) >>> warped_image = map_coordinates(image, coords)
- skimage.transform.warp_polar(image, center=None, *, radius=None, output_shape=None, scaling='linear', channel_axis=None, **kwargs)[source]#
画像を極座標または対数極座標空間にリマップします。
- パラメータ:
- image(M, N[, C]) ndarray
入力画像。マルチチャネル画像の場合、
channel_axisを指定する必要があります。- center2要素タプル, optional
image内の変換の中心を表すポイントの(行, 列)座標 (つまり、デカルト空間の原点)。値はfloat型にすることができます。値が指定されていない場合、中心はimageの中心点であると見なされます。- radiusfloat, optional
変換する領域を囲む円の半径。
- output_shapeタプル (行, 列), optional
- scaling{'linear', 'log'}, optional
画像ワーピングが極座標か対数極座標かを指定します。デフォルトは 'linear' です。
- channel_axisint または None, optional
None の場合、画像はグレースケール(シングルチャンネル)画像とみなされます。それ以外の場合、このパラメーターは配列のどの軸がチャンネルに対応するかを示します。
バージョン 0.19 で追加:
channel_axisが 0.19 で追加されました。- **kwargsキーワード引数
transform.warpに渡されます。
- 戻り値:
- warpedndarray
極座標または対数極座標でワーピングされた画像。
サンプル
グレースケール画像に基本的な極座標ワーピングを実行します
>>> from skimage import data >>> from skimage.transform import warp_polar >>> image = data.checkerboard() >>> warped = warp_polar(image)
グレースケール画像に対数極座標ワーピングを実行します
>>> warped = warp_polar(image, scaling='log')
中心、半径、および出力形状を指定しながら、グレースケール画像に対数極座標ワーピングを実行します
>>> warped = warp_polar(image, (100,100), radius=100, ... output_shape=image.shape, scaling='log')
カラー画像に対数極座標ワーピングを実行します
>>> image = data.astronaut() >>> warped = warp_polar(image, scaling='log', channel_axis=-1)
- class skimage.transform.AffineTransform(matrix=None, scale=None, rotation=None, shear=None, translation=None, *, dimensionality=2)[source]#
基底クラス:
ProjectiveTransformアフィン変換。
次の形式を持ちます
X = a0 * x + a1 * y + a2 = sx * x * [cos(rotation) + tan(shear_y) * sin(rotation)] - sy * y * [tan(shear_x) * cos(rotation) + sin(rotation)] + translation_x Y = b0 * x + b1 * y + b2 = sx * x * [sin(rotation) - tan(shear_y) * cos(rotation)] - sy * y * [tan(shear_x) * sin(rotation) - cos(rotation)] + translation_y
ここで、
sxとsyは x および y 方向のスケールファクターです。これは、次の順序で操作を適用することと同等です
スケール
シア
回転
平行移動
同次変換行列は次のとおりです
[[a0 a1 a2] [b0 b1 b2] [0 0 1]]
2Dでは、変換パラメータは、上記の同次変換行列として、または暗黙的なパラメータであるスケール、回転、シア、およびx(a2)とy(b2)の平行移動として与えることができます。3D以上では、行列形式のみが許可されます。
ユークリッド変換(回転と平行移動のみ)や類似変換(回転、平行移動、グローバルスケールファクター)など、より狭い変換では、暗黙的なパラメータを使用して3D変換を指定することも可能です。
- パラメータ:
- matrix(D+1, D+1) array_like, optional
同次変換行列。この行列が提供されている場合、スケール、回転、シア、または平行移動のいずれかを提供することはエラーになります。
- scale{s (float) または (sx, sy) (array, list, tuple)}, optional
スケールファクター。単一の値の場合、sx と sy の両方に割り当てられます。2Dでのみ利用可能です。
バージョン 0.17 で追加: 単一のスカラー値を提供するサポートを追加しました。
- rotationfloat, optional
回転角、時計回り、ラジアン単位。2Dでのみ利用可能です。
- shearfloat または float の 2要素タプル, optional
原点を中心にこれらの軸が回転する時計回りの x および y のシア角[2]。単一の値が指定された場合、それを x のシア角とし、y の角度は 0 のままにします。2Dでのみ利用可能です。
- translation(tx, ty) (array, list, tuple), optional
平行移動パラメータ。2Dでのみ利用可能です。
- dimensionalityint, optional
変換の次元。他のパラメータが提供されている場合は使用されません。
- 属性:
- params(D+1, D+1) 配列
同次変換行列。
- 発生する例外:
- ValueError
matrixとその他のパラメータのいずれかが提供されている場合。
参考文献
[1]Wikipedia, “Affine transformation”, https://en.wikipedia.org/wiki/Affine_transformation#Image_transformation
[2]Wikipedia, “Shear mapping”, https://en.wikipedia.org/wiki/Shear_mapping
サンプル
>>> import numpy as np >>> import skimage as ski >>> img = ski.data.astronaut()
ソースポイントとデスティネーションポイントを定義します
>>> src = np.array([[150, 150], ... [250, 100], ... [150, 200]]) >>> dst = np.array([[200, 200], ... [300, 150], ... [150, 400]])
変換行列を推定します
>>> tform = ski.transform.AffineTransform() >>> tform.estimate(src, dst) True
変換を適用します
>>> warped = ski.transform.warp(img, inverse_map=tform.inverse)
- __init__(matrix=None, scale=None, rotation=None, shear=None, translation=None, *, dimensionality=2)[source]#
- property dimensionality#
変換の次元。
- estimate(src, dst, weights=None)[source]#
対応するポイントのセットから変換を推定します。
全最小二乗法を使用して、過決定、適決定、および過小決定パラメータを決定できます。
ソース座標と宛先座標の数は一致する必要があります。
変換は次のように定義されます
X = (a0*x + a1*y + a2) / (c0*x + c1*y + 1) Y = (b0*x + b1*y + b2) / (c0*x + c1*y + 1)
これらの式は、次の形式に変換できます
0 = a0*x + a1*y + a2 - c0*x*X - c1*y*X - X 0 = b0*x + b1*y + b2 - c0*x*Y - c1*y*Y - Y
これは、対応する各ポイントのセットに存在するため、N * 2 個の方程式のセットがあります。係数は線形に現れるため、A x = 0 と書くことができ、ここで
A = [[x y 1 0 0 0 -x*X -y*X -X] [0 0 0 x y 1 -x*Y -y*Y -Y] ... ... ] x.T = [a0 a1 a2 b0 b1 b2 c0 c1 c3]
総最小二乗法の場合、この同次方程式系の解は、係数c3で正規化された、Aの最小特異値に対応する右特異ベクトルになります。
各対応点ペアに重みを適用することで、特に過決定系において、点ペアの信頼性や関連する不確かさの高低を示すことができます。最小二乗問題の行列処理では、これらの重み値は正規化され、平方根が取られ、対角行列に組み込まれ、それによってAが乗算されます。
アフィン変換の場合、係数c0とc1は0です。したがって、方程式系は次のようになります。
A = [[x y 1 0 0 0 -X] [0 0 0 x y 1 -Y] ... ... ] x.T = [a0 a1 a2 b0 b1 b2 c3]
- パラメータ:
- src(N, 2) array_like
ソース座標。
- dst(N, 2) array_like
デスティネーション座標。
- weights(N,) array_like, optional
各点ペアの相対的な重み値。
- 戻り値:
- successbool
モデル推定が成功した場合はTrue。
- property inverse#
逆変換を表す変換オブジェクトを返します。
- residuals(src, dst)[ソース]#
変換されたデスティネーション座標の残差を決定します。
変換された各ソース座標について、対応するデスティネーション座標までのユークリッド距離が決定されます。
- パラメータ:
- src(N, 2) array
ソース座標。
- dst(N, 2) array
デスティネーション座標。
- 戻り値:
- residuals(N,) array
座標の残差。
- property rotation#
- property scale#
- property shear#
- property translation#
- class skimage.transform.EssentialMatrixTransform(rotation=None, translation=None, matrix=None, *, dimensionality=2)[ソース]#
ベースクラス:
FundamentalMatrixTransform本質行列変換。
エッセンシャル行列は、キャリブレーションされた画像のペア間の対応点を関連付けます。この行列は、ある画像内の正規化された同次画像点を、もう一方の画像内のエピポーラ線に変換します。
エッセンシャル行列は、非平面シーンをキャプチャする移動画像のペアに対してのみ定義されます。純粋な回転または平面シーンの場合、ホモグラフィーが2つの画像間の幾何学的関係を記述します(
ProjectiveTransform)。画像の内部キャリブレーションが不明な場合、基礎行列が2つの画像間の射影関係を記述します(FundamentalMatrixTransform)。- パラメータ:
- rotation(3, 3) array_like, optional
相対的なカメラモーションの回転行列。
- translation(3, 1) array_like, optional
相対的なカメラモーションの並進ベクトル。ベクトルは単位長である必要があります。
- matrix(3, 3) array_like, optional
エッセンシャル行列。
- 属性:
- params(3, 3) array
エッセンシャル行列。
参考文献
[1]Hartley, Richard, and Andrew Zisserman. Multiple view geometry in computer vision. Cambridge university press, 2003.
サンプル
>>> import numpy as np >>> import skimage as ski >>> >>> tform_matrix = ski.transform.EssentialMatrixTransform( ... rotation=np.eye(3), translation=np.array([0, 0, 1]) ... ) >>> tform_matrix.params array([[ 0., -1., 0.], [ 1., 0., 0.], [ 0., 0., 0.]]) >>> src = np.array([[ 1.839035, 1.924743], ... [ 0.543582, 0.375221], ... [ 0.47324 , 0.142522], ... [ 0.96491 , 0.598376], ... [ 0.102388, 0.140092], ... [15.994343, 9.622164], ... [ 0.285901, 0.430055], ... [ 0.09115 , 0.254594]]) >>> dst = np.array([[1.002114, 1.129644], ... [1.521742, 1.846002], ... [1.084332, 0.275134], ... [0.293328, 0.588992], ... [0.839509, 0.08729 ], ... [1.779735, 1.116857], ... [0.878616, 0.602447], ... [0.642616, 1.028681]]) >>> tform_matrix.estimate(src, dst) True >>> tform_matrix.residuals(src, dst) array([0.42455187, 0.01460448, 0.13847034, 0.12140951, 0.27759346, 0.32453118, 0.00210776, 0.26512283])
- estimate(src, dst)[ソース]#
8点アルゴリズムを使用してエッセンシャル行列を推定します。
8点アルゴリズムでは、十分に条件付けられた解を得るためには少なくとも8つの対応する点ペアが必要です。そうでない場合は、過決定解が推定されます。
- パラメータ:
- src(N, 2) array_like
ソース座標。
- dst(N, 2) array_like
デスティネーション座標。
- 戻り値:
- successbool
モデル推定が成功した場合はTrue。
- property inverse#
逆変換を表す変換オブジェクトを返します。
F.Tが逆になる理由については、Hartley & Zisserman, Ch. 8: Epipolar Geometry and the Fundamental Matrixを参照してください。
- class skimage.transform.EuclideanTransform(matrix=None, rotation=None, translation=None, *, dimensionality=2)[ソース]#
基底クラス:
ProjectiveTransformユークリッド変換(剛体変換とも呼ばれます)。
次の形式を持ちます
X = a0 * x - b0 * y + a1 = = x * cos(rotation) - y * sin(rotation) + a1 Y = b0 * x + a0 * y + b1 = = x * sin(rotation) + y * cos(rotation) + b1
ここで、同次変換行列は次のようになります。
[[a0 -b0 a1] [b0 a0 b1] [0 0 1 ]]
ユークリッド変換は、回転と並進のパラメーターを持つ剛体変換です。相似変換は、ユークリッド変換を単一のスケーリングファクターで拡張します。
2Dおよび3Dでは、変換パラメーターは、上記の同次変換行列である
matrix、または暗黙的なパラメーターrotationおよび/またはtranslation(ここでa1はxに沿った並進、b1はyに沿った並進など)を介して提供できます。3Dを超えて、変換が並進のみである場合は、暗黙的なパラメーターtranslationを使用できます。それ以外の場合は、matrixを使用する必要があります。- パラメータ:
- matrix(D+1, D+1) array_like, optional
同次変換行列。
- rotationfloat または float のシーケンス, optional
回転角(時計回り、ラジアン単位)。ベクトルとして指定された場合は、オイラー回転角[1]として解釈されます。2D(単一回転)および3D(オイラー回転)の値のみがサポートされています。高次元の場合、変換行列を提供または推定する必要があります。
- translation(x, y[, z, …]) float のシーケンス, 長さ D, optional
各軸の並進パラメーター。
- dimensionalityint, optional
変換の次元数。
- 属性:
- params(D+1, D+1) 配列
同次変換行列。
参考文献
- プロパティ dimensionality#
変換の次元。
- estimate(src, dst)[ソース]#
対応するポイントのセットから変換を推定します。
全最小二乗法を使用して、過決定、適決定、および過小決定パラメータを決定できます。
ソース座標と宛先座標の数は一致する必要があります。
- パラメータ:
- src(N, 2) array_like
ソース座標。
- dst(N, 2) array_like
デスティネーション座標。
- 戻り値:
- successbool
モデル推定が成功した場合はTrue。
- プロパティ inverse#
逆変換を表す変換オブジェクトを返します。
- residuals(src, dst)[ソース]#
変換されたデスティネーション座標の残差を決定します。
変換された各ソース座標について、対応するデスティネーション座標までのユークリッド距離が決定されます。
- パラメータ:
- src(N, 2) array
ソース座標。
- dst(N, 2) array
デスティネーション座標。
- 戻り値:
- residuals(N,) array
座標の残差。
- プロパティ rotation#
- プロパティ translation#
- クラス skimage.transform.FundamentalMatrixTransform(matrix=None, *, dimensionality=2)[ソース]#
ベース:
_GeometricTransform基本行列変換。
基本行列は、キャリブレーションされていない一対の画像間で対応する点を関連付けます。この行列は、ある画像の同次座標の点を別の画像の極線に変換します。
基本行列は、動いている画像ペアに対してのみ定義されます。純粋な回転や平面シーンの場合、ホモグラフィーは2つの画像間の幾何学的関係を記述します(
ProjectiveTransform)。画像の内部キャリブレーションが既知の場合、本質行列は2つの画像間のメトリック関係を記述します(EssentialMatrixTransform)。- パラメータ:
- matrix(3, 3) array_like, optional
基本行列。
- 属性:
- params(3, 3) array
基本行列。
参考文献
[1]Hartley, Richard, and Andrew Zisserman. Multiple view geometry in computer vision. Cambridge university press, 2003.
サンプル
>>> import numpy as np >>> import skimage as ski >>> tform_matrix = ski.transform.FundamentalMatrixTransform()
ソースポイントとデスティネーションポイントを定義します
>>> src = np.array([1.839035, 1.924743, ... 0.543582, 0.375221, ... 0.473240, 0.142522, ... 0.964910, 0.598376, ... 0.102388, 0.140092, ... 15.994343, 9.622164, ... 0.285901, 0.430055, ... 0.091150, 0.254594]).reshape(-1, 2) >>> dst = np.array([1.002114, 1.129644, ... 1.521742, 1.846002, ... 1.084332, 0.275134, ... 0.293328, 0.588992, ... 0.839509, 0.087290, ... 1.779735, 1.116857, ... 0.878616, 0.602447, ... 0.642616, 1.028681]).reshape(-1, 2)
変換行列を推定します
>>> tform_matrix.estimate(src, dst) True >>> tform_matrix.params array([[-0.21785884, 0.41928191, -0.03430748], [-0.07179414, 0.04516432, 0.02160726], [ 0.24806211, -0.42947814, 0.02210191]])
サンプソン距離を計算します
>>> tform_matrix.residuals(src, dst) array([0.0053886 , 0.00526101, 0.08689701, 0.01850534, 0.09418259, 0.00185967, 0.06160489, 0.02655136])
逆変換を適用します
>>> tform_matrix.inverse(dst) array([[-0.0513591 , 0.04170974, 0.01213043], [-0.21599496, 0.29193419, 0.00978184], [-0.0079222 , 0.03758889, -0.00915389], [ 0.14187184, -0.27988959, 0.02476507], [ 0.05890075, -0.07354481, -0.00481342], [-0.21985267, 0.36717464, -0.01482408], [ 0.01339569, -0.03388123, 0.00497605], [ 0.03420927, -0.1135812 , 0.02228236]])
- estimate(src, dst)[ソース]#
8点アルゴリズムを使用して基本行列を推定します。
8点アルゴリズムでは、十分に条件付けられた解を得るためには少なくとも8つの対応する点ペアが必要です。そうでない場合は、過決定解が推定されます。
- パラメータ:
- src(N, 2) array_like
ソース座標。
- dst(N, 2) array_like
デスティネーション座標。
- 戻り値:
- successbool
モデル推定が成功した場合はTrue。
- プロパティ inverse#
逆変換を表す変換オブジェクトを返します。
F.Tが逆になる理由については、Hartley & Zisserman, Ch. 8: Epipolar Geometry and the Fundamental Matrixを参照してください。
- クラス skimage.transform.PiecewiseAffineTransform[ソース]#
ベース:
_GeometricTransform区分アフィン変換。
制御点は、マッピングを定義するために使用されます。この変換は、点をメッシュにするためのドロネー三角形分割に基づいています。各三角形は、ローカルアフィン変換を見つけるために使用されます。
- 属性:
- affinesAffineTransformオブジェクトのリスト
メッシュ内の各三角形のアフィン変換。
- inverse_affinesAffineTransformオブジェクトのリスト
メッシュ内の各三角形の逆アフィン変換。
- estimate(src, dst)[ソース]#
対応するポイントのセットから変換を推定します。
ソース座標と宛先座標の数は一致する必要があります。
- パラメータ:
- src(N, D) array_like
ソース座標。
- dst(N, D) array_like
デスティネーション座標。
- 戻り値:
- successbool
モデルのすべての部分が正常に推定された場合はTrue。
- プロパティ inverse#
逆変換を表す変換オブジェクトを返します。
- クラス skimage.transform.PolynomialTransform(params=None, *, dimensionality=2)[ソース]#
ベース:
_GeometricTransform2D多項式変換。
次の形式を持ちます
X = sum[j=0:order]( sum[i=0:j]( a_ji * x**(j - i) * y**i )) Y = sum[j=0:order]( sum[i=0:j]( b_ji * x**(j - i) * y**i ))
- パラメータ:
- params(2, N) array_like, オプション
多項式係数。ここで、
N * 2 = (order + 1) * (order + 2)です。したがって、a_jiはparams[0, :]で定義され、b_jiはparams[1, :]で定義されます。
- 属性:
- params(2, N) 配列
多項式係数。ここで、
N * 2 = (order + 1) * (order + 2)です。したがって、a_jiはparams[0, :]で定義され、b_jiはparams[1, :]で定義されます。
- estimate(src, dst, order=2, weights=None)[ソース]#
対応するポイントのセットから変換を推定します。
全最小二乗法を使用して、過決定、適決定、および過小決定パラメータを決定できます。
ソース座標と宛先座標の数は一致する必要があります。
変換は次のように定義されます
X = sum[j=0:order]( sum[i=0:j]( a_ji * x**(j - i) * y**i )) Y = sum[j=0:order]( sum[i=0:j]( b_ji * x**(j - i) * y**i ))
これらの式は、次の形式に変換できます
0 = sum[j=0:order]( sum[i=0:j]( a_ji * x**(j - i) * y**i )) - X 0 = sum[j=0:order]( sum[i=0:j]( b_ji * x**(j - i) * y**i )) - Y
これは、対応する各ポイントのセットに存在するため、N * 2 個の方程式のセットがあります。係数は線形に現れるため、A x = 0 と書くことができ、ここで
A = [[1 x y x**2 x*y y**2 ... 0 ... 0 -X] [0 ... 0 1 x y x**2 x*y y**2 -Y] ... ... ] x.T = [a00 a10 a11 a20 a21 a22 ... ann b00 b10 b11 b20 b21 b22 ... bnn c3]
総最小二乗法の場合、この同次方程式系の解は、係数c3で正規化された、Aの最小特異値に対応する右特異ベクトルになります。
各対応点ペアに重みを適用することで、特に過決定系において、点ペアの信頼性や関連する不確かさの高低を示すことができます。最小二乗問題の行列処理では、これらの重み値は正規化され、平方根が取られ、対角行列に組み込まれ、それによってAが乗算されます。
- パラメータ:
- src(N, 2) array_like
ソース座標。
- dst(N, 2) array_like
デスティネーション座標。
- orderint, オプション
多項式の次数(係数の数は次数+ 1です)。
- weights(N,) array_like, optional
各点ペアの相対的な重み値。
- 戻り値:
- successbool
モデル推定が成功した場合はTrue。
- プロパティ inverse#
逆変換を表す変換オブジェクトを返します。
- class skimage.transform.ProjectiveTransform(matrix=None, *, dimensionality=2)[source]#
ベース:
_GeometricTransform射影変換。
座標に射影変換(ホモグラフィー)を適用します。
各同次座標 \(\mathbf{x} = [x, y, 1]^T\) について、その目標位置は、与えられた行列 \(H\) を掛けることによって計算され、\(H \mathbf{x}\) が得られます。
[[a0 a1 a2] [b0 b1 b2] [c0 c1 1 ]].
例えば、theta度時計回りに回転させるには、行列は次のようになります。
[[cos(theta) -sin(theta) 0] [sin(theta) cos(theta) 0] [0 0 1]]
または、xを10、yを20だけ平行移動するには、次のようになります。
[[1 0 10] [0 1 20] [0 0 1 ]].
- パラメータ:
- matrix(D+1, D+1) array_like, optional
同次変換行列。
- dimensionalityint, optional
変換の次元数。
matrixが None でない場合は無視されます。
- 属性:
- params(D+1, D+1) 配列
同次変換行列。
- property dimensionality#
変換の次元。
- estimate(src, dst, weights=None)[source]#
対応するポイントのセットから変換を推定します。
全最小二乗法を使用して、過決定、適決定、および過小決定パラメータを決定できます。
ソース座標と宛先座標の数は一致する必要があります。
変換は次のように定義されます
X = (a0*x + a1*y + a2) / (c0*x + c1*y + 1) Y = (b0*x + b1*y + b2) / (c0*x + c1*y + 1)
これらの式は、次の形式に変換できます
0 = a0*x + a1*y + a2 - c0*x*X - c1*y*X - X 0 = b0*x + b1*y + b2 - c0*x*Y - c1*y*Y - Y
これは、対応する各ポイントのセットに存在するため、N * 2 個の方程式のセットがあります。係数は線形に現れるため、A x = 0 と書くことができ、ここで
A = [[x y 1 0 0 0 -x*X -y*X -X] [0 0 0 x y 1 -x*Y -y*Y -Y] ... ... ] x.T = [a0 a1 a2 b0 b1 b2 c0 c1 c3]
総最小二乗法の場合、この同次方程式系の解は、係数c3で正規化された、Aの最小特異値に対応する右特異ベクトルになります。
各対応点ペアに重みを適用することで、特に過決定系において、点ペアの信頼性や関連する不確かさの高低を示すことができます。最小二乗問題の行列処理では、これらの重み値は正規化され、平方根が取られ、対角行列に組み込まれ、それによってAが乗算されます。
アフィン変換の場合、係数c0とc1は0です。したがって、方程式系は次のようになります。
A = [[x y 1 0 0 0 -X] [0 0 0 x y 1 -Y] ... ... ] x.T = [a0 a1 a2 b0 b1 b2 c3]
- パラメータ:
- src(N, 2) array_like
ソース座標。
- dst(N, 2) array_like
デスティネーション座標。
- weights(N,) array_like, optional
各点ペアの相対的な重み値。
- 戻り値:
- successbool
モデル推定が成功した場合はTrue。
- property inverse#
逆変換を表す変換オブジェクトを返します。
- class skimage.transform.SimilarityTransform(matrix=None, scale=None, rotation=None, translation=None, *, dimensionality=2)[source]#
ベース:
EuclideanTransform相似変換。
2Dでは次の形式を持ちます
X = a0 * x - b0 * y + a1 = = s * x * cos(rotation) - s * y * sin(rotation) + a1 Y = b0 * x + a0 * y + b1 = = s * x * sin(rotation) + s * y * cos(rotation) + b1
ここで、
sはスケールファクターであり、同次変換行列は[[a0 -b0 a1] [b0 a0 b1] [0 0 1 ]]
相似変換は、回転および平行移動パラメータに加えて、単一のスケーリングファクターでユークリッド変換を拡張します。
- パラメータ:
- matrix(dim+1, dim+1) array_like, optional
同次変換行列。
- scalefloat, optional
スケールファクター。2Dおよび3Dのみに実装されています。
- rotationfloat, optional
回転角、時計回り、ラジアン単位。2Dおよび3Dのみに実装されています。3Dの場合、これはZYXオイラー角で与えられます。
- translation(dim,) array_like, optional
x, y[, z] 平行移動パラメータ。2Dおよび3Dのみに実装されています。
- 属性:
- params(dim+1, dim+1) array
同次変換行列。
- property dimensionality#
変換の次元。
- estimate(src, dst)[source]#
対応するポイントのセットから変換を推定します。
全最小二乗法を使用して、過決定、適決定、および過小決定パラメータを決定できます。
ソース座標と宛先座標の数は一致する必要があります。
- パラメータ:
- src(N, 2) array_like
ソース座標。
- dst(N, 2) array_like
デスティネーション座標。
- 戻り値:
- successbool
モデル推定が成功した場合はTrue。
- property inverse#
逆変換を表す変換オブジェクトを返します。
- residuals(src, dst)[source]#
変換されたデスティネーション座標の残差を決定します。
変換された各ソース座標について、対応するデスティネーション座標までのユークリッド距離が決定されます。
- パラメータ:
- src(N, 2) array
ソース座標。
- dst(N, 2) array
デスティネーション座標。
- 戻り値:
- residuals(N,) array
座標の残差。
- property rotation#
- property scale#
- property translation#
- class skimage.transform.ThinPlateSplineTransform[source]#
ベース:
object薄板スプライン変換。
ソースと宛先の2組の一致する点が与えられた場合、このクラスは、ソース内の各点を宛先に対応するものに変換する薄板スプライン(TPS)変換を推定します。
- 属性:
- src(N, 2) array_like
ソース画像内の制御点の座標。
参考文献
[1]Bookstein, Fred L. “Principal warps: Thin-plate splines and the decomposition of deformations,” IEEE Transactions on pattern analysis and machine intelligence 11.6 (1989): 567–585. DOI:
10.1109/34.24792https://user.engineering.uiowa.edu/~aip/papers/bookstein-89.pdfサンプル
>>> import skimage as ski
90度回転をシミュレートするようにソースおよび宛先の制御点を定義し、それらからメッシュグリッドを生成します。
>>> src = np.array([[0, 0], [0, 5], [5, 5], [5, 0]]) >>> dst = np.array([[5, 0], [0, 0], [0, 5], [5, 5]])
変換を推定します。
>>> tps = ski.transform.ThinPlateSplineTransform() >>> tps.estimate(src, dst) True
srcに変換を適用すると、dstが近似されます。>>> np.round(tps(src)) array([[5., 0.], [0., 0.], [0., 5.], [5., 5.]])
変換を適用するためのメッシュグリッドを作成します。
>>> grid = np.meshgrid(np.arange(5), np.arange(5)) >>> grid[1] array([[0, 0, 0, 0, 0], [1, 1, 1, 1, 1], [2, 2, 2, 2, 2], [3, 3, 3, 3, 3], [4, 4, 4, 4, 4]])
>>> coords = np.vstack([grid[0].ravel(), grid[1].ravel()]).T >>> transformed = tps(coords) >>> np.round(transformed[:, 1]).reshape(5, 5).astype(int) array([[0, 1, 2, 3, 4], [0, 1, 2, 3, 4], [0, 1, 2, 3, 4], [0, 1, 2, 3, 4], [0, 1, 2, 3, 4]])
- estimate(src, dst)[source]#
ソース点と宛先点の間の最適なスプラインマッピングを推定します。
- パラメータ:
- src(N, 2) array_like
ソース座標での制御点。
- dst(N, 2) array_like
宛先座標での制御点。
- 戻り値:
- success: bool
True は推定が成功したことを示します。
注
ソース点と宛先点の数 N は一致する必要があります。
- property inverse#