skimage.morphology#
モルフォロジーアルゴリズム、例えば、クロージング、オープニング、スケルトン化など。
画像の面積クロージングを実行します。 |
|
画像の面積オープニングを実行します。 |
|
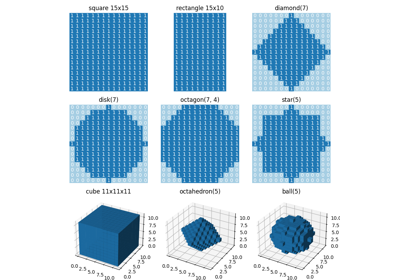
球状のフットプリントを生成します。 |
|
画像の高速なバイナリモルフォロジークロージングを返します。 |
|
画像の高速なバイナリモルフォロジー膨張を返します。 |
|
画像の高速なバイナリモルフォロジー収縮を返します。 |
|
画像の高速なバイナリモルフォロジーオープニングを返します。 |
|
画像のブラックトップハットを返します。 |
|
画像のグレースケールモルフォロジークロージングを返します。 |
|
バイナリ画像の凸包画像を計算します。 |
|
バイナリ画像内の個々のオブジェクトの凸包画像を計算します。 |
|
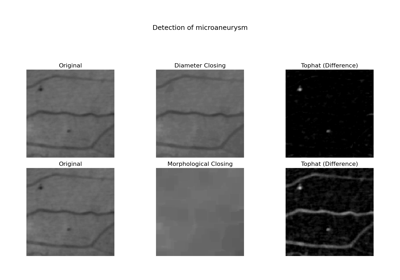
画像の直径クロージングを実行します。 |
|
画像の直径オープニングを実行します。 |
|
平坦なダイヤモンド型のフットプリントを生成します。 |
|
画像のグレースケールモルフォロジー膨張を返します。 |
|
平坦な円盤型のフットプリントを生成します。 |
|
平坦な楕円形のフットプリントを生成します。 |
|
画像のグレースケールモルフォロジー収縮を返します。 |
|
フラッドフィルに対応するマスク。 |
|
画像にフラッドフィルを実行します。 |
|
フットプリントシーケンスを等価なndarrayに変換します。 |
|
矩形または超矩形のフットプリントを生成します。 |
|
高さ>= hの画像のすべての極大値を決定します。 |
|
深さ>= hの画像のすべての極小値を決定します。 |
|
画像のバイナリモルフォロジークロージングを返します。 |
|
画像のバイナリモルフォロジー膨張を返します。 |
|
画像のバイナリモルフォロジー収縮を返します。 |
|
画像のバイナリモルフォロジーオープニングを返します。 |
|
整数配列の連結領域にラベルを付けます。 |
|
n次元配列の局所的最大値を見つけます。 |
|
n次元配列の局所的最小値を見つけます。 |
|
画像から最大ツリーを構築します。 |
|
画像のすべての局所的最大値を決定します。 |
|
バイナリ画像の中軸変換を計算します。 |
|
フットプリントの各次元を反転します。 |
|
八角形のフットプリントを生成します。 |
|
八面体型のフットプリントを生成します。 |
|
画像のグレースケールモルフォロジーオープニングを返します。 |
|
フットプリントを各次元で奇数サイズにパディングします。 |
|
画像のモルフォロジー再構成を実行します。 |
|
残りのオブジェクトが最小距離離れるまで、指定された順序でオブジェクトを削除します。 |
|
指定されたサイズより小さい連続した穴を削除します。 |
|
指定されたサイズより小さいオブジェクトを削除します。 |
|
間引きによって入力画像のスケルトンを計算します。 |
|
星型のフットプリントを生成します。 |
|
バイナリ画像のモルフォロジー細線化を実行します。 |
|
画像のホワイトトップハットを返します。 |
- skimage.morphology.area_closing(image, area_threshold=64, connectivity=1, parent=None, tree_traverser=None)[source]#
画像の面積クロージングを実行します。
面積クロージングは、表面積が area_threshold より小さい画像のすべての暗い構造を削除します。出力画像は、すべてのピクセルについて入力画像以上であり、すべての局所的最小値は少なくとも area_threshold ピクセルの表面積を持ちます。
面積クロージングはモルフォロジークロージングに似ていますが、固定フットプリントを使用するのではなく、表面積 = area_threshold の変形可能なフットプリントを使用します。
バイナリの場合、面積クロージングは remove_small_holes と同等です。したがって、この演算子はグレースケール画像に拡張されます。
技術的には、この演算子は画像の最大ツリー表現に基づいています。
- パラメータ:
- **image**: ndarray
area_closing を計算する入力画像。この画像は任意の型にすることができます。
- **area_threshold**: 符号なし整数
サイズパラメータ(ピクセル数)。デフォルト値は任意に64に選択されます。
- **connectivity**: 符号なし整数、オプション
近傍接続性。整数は、隣接に到達するための直交ステップの最大数を表します。2Dでは、4近傍の場合は1、8近傍の場合は2です。デフォルト値は1です。
- **parent**: ndarray、int64、オプション
反転画像の最大ツリーを表す親画像。各ピクセルの値は、ravelled配列における親のインデックスです。詳細は注記を参照してください。
- **tree_traverser**: 1D配列、int64、オプション
順序付けられたピクセルインデックス(ravelled配列を参照)。ピクセルは、すべてのピクセルがその親の前に来るように順序付けられます(親のないルートを除く)。
- 戻り値:
- **output**: ndarray
入力画像と同じ形状と型の出力画像。
参照
注記
最大ツリー表現(parentとtree_traverser)が関数に与えられる場合、この関数の反転画像から計算する必要があります。つまり、>>> P, S = max_tree(invert(f)) >>> closed = diameter_closing(f, 3, parent=P, tree_traverser=S)
参考文献
[1]Vincent L., Proc. “Grayscale area openings and closings, their efficient implementation and applications”, EURASIP Workshop on Mathematical Morphology and its Applications to Signal Processing, Barcelona, Spain, pp.22-27, May 1993.
[2]Soille, P., “Morphological Image Analysis: Principles and Applications” (Chapter 6), 2nd edition (2003), ISBN 3540429883. DOI:10.1007/978-3-662-05088-0
[3]Salembier, P., Oliveras, A., & Garrido, L. (1998). Antiextensive Connected Operators for Image and Sequence Processing. IEEE Transactions on Image Processing, 7(4), 555-570. DOI:10.1109/83.663500
[4]Najman, L., & Couprie, M. (2006). Building the component tree in quasi-linear time. IEEE Transactions on Image Processing, 15(11), 3531-3539. DOI:10.1109/TIP.2006.877518
[5]Carlinet, E., & Geraud, T. (2014). A Comparative Review of Component Tree Computation Algorithms. IEEE Transactions on Image Processing, 23(9), 3885-3895. DOI:10.1109/TIP.2014.2336551
例
画像を作成します(中心に最小値、さらに4つの局所的最小値を持つ二次関数)。
>>> w = 12 >>> x, y = np.mgrid[0:w,0:w] >>> f = 180 + 0.2*((x - w/2)**2 + (y-w/2)**2) >>> f[2:3,1:5] = 160; f[2:4,9:11] = 140; f[9:11,2:4] = 120 >>> f[9:10,9:11] = 100; f[10,10] = 100 >>> f = f.astype(int)
面積クロージングを計算できます
>>> closed = area_closing(f, 8, connectivity=1)
すべての小さな最小値が削除され、残りの最小値は少なくともサイズ8になります。
- skimage.morphology.area_opening(image, area_threshold=64, connectivity=1, parent=None, tree_traverser=None)[source]#
画像の面積オープニングを実行します。
面積オープニングは、表面積が area_threshold より小さい画像のすべての明るい構造を削除します。したがって、出力画像は、すべての局所的最大値が少なくとも area_threshold ピクセルの表面積を持つ入力画像より小さい最大の画像です。
面積オープニングはモルフォロジーオープニングに似ていますが、固定フットプリントを使用するのではなく、表面積 = area_threshold の変形可能なフットプリントを使用します。したがって、area_threshold=1 の面積オープニングは恒等変換です。
バイナリの場合、面積オープニングは remove_small_objects と同等です。したがって、この演算子はグレースケール画像に拡張されます。
技術的には、この演算子は画像の最大ツリー表現に基づいています。
- パラメータ:
- **image**: ndarray
area_opening を計算する入力画像。この画像は任意の型にすることができます。
- **area_threshold**: 符号なし整数
サイズパラメータ(ピクセル数)。デフォルト値は任意に64に選択されます。
- **connectivity**: 符号なし整数、オプション
近傍接続性。整数は、隣接に到達するための直交ステップの最大数を表します。2Dでは、4近傍の場合は1、8近傍の場合は2です。デフォルト値は1です。
- **parent**: ndarray、int64、オプション
画像の最大ツリーを表す親画像。各ピクセルの値は、ravelled配列における親のインデックスです。
- **tree_traverser**: 1D配列、int64、オプション
順序付けられたピクセルインデックス(ravelled配列を参照)。ピクセルは、すべてのピクセルがその親の前に来るように順序付けられます(親のないルートを除く)。
- 戻り値:
- **output**: ndarray
入力画像と同じ形状と型の出力画像。
参照
参考文献
[1]Vincent L., Proc. “Grayscale area openings and closings, their efficient implementation and applications”, EURASIP Workshop on Mathematical Morphology and its Applications to Signal Processing, Barcelona, Spain, pp.22-27, May 1993.
[2]Soille, P., “Morphological Image Analysis: Principles and Applications” (Chapter 6), 2nd edition (2003), ISBN 3540429883. DOI:10.1007/978-3-662-05088-0
[3]Salembier, P., Oliveras, A., & Garrido, L. (1998). Antiextensive Connected Operators for Image and Sequence Processing. IEEE Transactions on Image Processing, 7(4), 555-570. DOI:10.1109/83.663500
[4]Najman, L., & Couprie, M. (2006). Building the component tree in quasi-linear time. IEEE Transactions on Image Processing, 15(11), 3531-3539. DOI:10.1109/TIP.2006.877518
[5]Carlinet, E., & Geraud, T. (2014). A Comparative Review of Component Tree Computation Algorithms. IEEE Transactions on Image Processing, 23(9), 3885-3895. DOI:10.1109/TIP.2014.2336551
例
画像を作成します(中心に最大値、さらに4つの局所的最大値を持つ二次関数)。
>>> w = 12 >>> x, y = np.mgrid[0:w,0:w] >>> f = 20 - 0.2*((x - w/2)**2 + (y-w/2)**2) >>> f[2:3,1:5] = 40; f[2:4,9:11] = 60; f[9:11,2:4] = 80 >>> f[9:10,9:11] = 100; f[10,10] = 100 >>> f = f.astype(int)
開口部の面積を計算できます。
>>> open = area_opening(f, 8, connectivity=1)
表面積が8未満のピークは削除されます。
- skimage.morphology.ball(radius, dtype=<class 'numpy.uint8'>, *, strict_radius=True, decomposition=None)[ソース]#
球状のフットプリントを生成します。
これは、ディスクの3次元版です。ピクセルは、原点とのユークリッド距離が半径以下であれば、近傍内にあります。
- パラメータ:
- radius浮動小数点数
球状フットプリントの半径。
- 戻り値:
- footprintndarray または タプル
近傍の要素が1、それ以外の要素が0であるフットプリント。
- その他の引数:
- dtypeデータ型、オプション
フットプリントのデータ型。
- strict_radius真偽値、オプション
Falseの場合、半径を0.5拡張します。これにより、円は、各軸に沿ってサイズが
2 * radius + 1のままである立方体内をさらに拡張できます。 decomposition が None でない場合、このパラメータは無視されます。- decomposition{None, 'sequence'}、オプション
Noneの場合、単一の配列が返されます。 'sequence'の場合、より小さなフットプリントのタプルが返されます。 この一連の小さなフットプリントを適用すると、単一の大きなフットプリントと同等の結果が得られますが、計算パフォーマンスが向上します。 ボールフットプリントの場合、シーケンス分解はdecomposition = Noneとまったく同じではありません。 詳細については、注意事項を参照してください。
注記
decomposition='sequence' モードで生成されるディスクは、decomposition=None のディスクと同じではありません。 ここでは、ディスクの [1] で採用されたアプローチを3次元の場合に拡張し、その出版物からの「正方形」、「ダイヤモンド」、「T字型」要素の3次元拡張を使用します。 これらの基本要素はすべてサイズ
(3,) * ndimです。 引数strict_radius=False, decomposition=Noneで計算されたボールに最も近い一致を与える各要素の繰り返し回数を数値的に計算しました。経験的に、シーケンス分解と同等の複合フットプリントは、斜方立方八面体(26面 [2])に近づきます。
参考文献
[1]Park, H and Chin R.T. Decomposition of structuring elements for optimal implementation of morphological operations. In Proceedings: 1997 IEEE Workshop on Nonlinear Signal and Image Processing, London, UK. https://www.iwaenc.org/proceedings/1997/nsip97/pdf/scan/ns970226.pdf
- skimage.morphology.binary_closing(image, footprint=None, out=None, *, mode='ignore')[ソース]#
画像の高速なバイナリモルフォロジークロージングを返します。
この関数は、グレースケールクロージングと同じ結果を返しますが、バイナリ画像の方が高速に実行されます。
画像のモルフォロジー的クロージングは、膨張に続いて収縮を行うものとして定義されます。 クロージングは、小さな暗い点(つまり「胡椒」)を取り除き、小さな明るい亀裂をつなぐことができます。 これは、(明るい)特徴間の(暗い)ギャップを「閉じる」傾向があります。
- パラメータ:
- **image**: ndarray
バイナリ入力画像。
- footprintndarray または タプル、オプション
1と0の2次元配列として表される近傍。 Noneの場合、十字型のフットプリント(connectivity = 1)を使用します。 フットプリントは、以下の注記で説明されているように、より小さなフットプリントのシーケンスとして提供することもできます。
- out真偽値のndarray、オプション
モルフォロジーの結果を格納する配列。 Noneが渡された場合は、新しい配列が割り当てられます。
- mode文字列、オプション
modeパラメータは、配列の境界をどのように処理するかを決定します。 有効なモードは、「max」、「min」、「ignore」です。 「ignore」の場合、画像ドメイン外のピクセルは、収縮の場合はTrue、膨張の場合はFalseであると想定されるため、結果に影響を与えません。 デフォルトは「ignore」です。バージョン0.23で追加:
modeは0.23で追加されました。
- 戻り値:
- closing真偽値のndarray
モルフォロジー的クロージングの結果。
注記
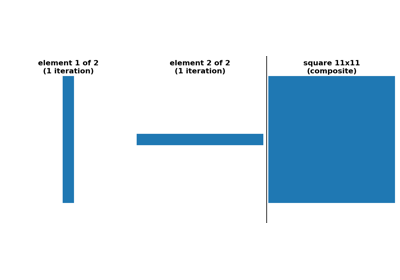
フットプリントは、2タプルのシーケンスとして提供することもできます。各2タプルの最初の要素はフットプリントndarrayで、2番目の要素は反復する回数を表す整数です。 たとえば、
footprint=[(np.ones((9, 1)), 1), (np.ones((1, 9)), 1)]は、9x1フットプリントに続いて1x9フットプリントを適用します。その結果、footprint=np.ones((9, 9))と同じ効果が得られますが、計算コストは低くなります。skimage.morphology.disk()などの組み込みフットプリントのほとんどは、このタイプのフットプリントシーケンスを自動的に生成するオプションを提供します。
- skimage.morphology.binary_dilation(image, footprint=None, out=None, *, mode='ignore')[ソース]#
画像の高速なバイナリモルフォロジー膨張を返します。
この関数は、グレースケール膨張と同じ結果を返しますが、バイナリ画像の方が高速に実行されます。
モルフォロジー的膨張は、
(i,j)のピクセルを、(i,j)を中心とする近傍のすべてのピクセルの最大値に設定します。 膨張は明るい領域を拡大し、暗い領域を縮小します。- パラメータ:
- **image**: ndarray
バイナリ入力画像。
- footprintndarray または タプル、オプション
1と0の2次元配列として表される近傍。 Noneの場合、十字型のフットプリント(connectivity = 1)を使用します。 フットプリントは、以下の注記で説明されているように、より小さなフットプリントのシーケンスとして提供することもできます。
- out真偽値のndarray、オプション
モルフォロジーの結果を格納する配列。 Noneが渡された場合は、新しい配列が割り当てられます。
- mode文字列、オプション
modeパラメータは、配列の境界をどのように処理するかを決定します。 有効なモードは、「max」、「min」、「ignore」です。 「min」または「ignore」の場合、画像ドメイン外のピクセルはFalseであると想定されるため、結果に影響を与えません。 デフォルトは「ignore」です。バージョン0.23で追加:
modeは0.23で追加されました。
- 戻り値:
- dilated真偽値またはuintのndarray
[False, True]の値を持つモルフォロジー的膨張の結果。
注記
フットプリントは、2タプルのシーケンスとして提供することもできます。各2タプルの最初の要素はフットプリントndarrayで、2番目の要素は反復する回数を表す整数です。 たとえば、
footprint=[(np.ones((9, 1)), 1), (np.ones((1, 9)), 1)]は、9x1フットプリントに続いて1x9フットプリントを適用します。その結果、footprint=np.ones((9, 9))と同じ効果が得られますが、計算コストは低くなります。skimage.morphology.disk()などの組み込みフットプリントのほとんどは、このタイプのフットプリントシーケンスを自動的に生成するオプションを提供します。非対称フットプリントの場合、
skimage.morphology.binary_dilation()とskimage.morphology.dilation()は異なる出力を生成します。binary_dilationはフットプリントをミラーリングしますが、dilationはミラーリングしません。
- skimage.morphology.binary_erosion(image, footprint=None, out=None, *, mode='ignore')[ソース]#
画像の高速なバイナリモルフォロジー収縮を返します。
この関数は、グレースケール収縮と同じ結果を返しますが、バイナリ画像の方が高速に実行されます。
モルフォロジー的収縮は、
(i,j)のピクセルを、(i,j)を中心とする近傍のすべてのピクセルの最小値に設定します。 収縮は明るい領域を縮小し、暗い領域を拡大します。- パラメータ:
- **image**: ndarray
バイナリ入力画像。
- footprintndarray または タプル、オプション
1と0の2次元配列として表される近傍。 Noneの場合、十字型のフットプリント(connectivity = 1)を使用します。 フットプリントは、以下の注記で説明されているように、より小さなフットプリントのシーケンスとして提供することもできます。
- out真偽値のndarray、オプション
モルフォロジーの結果を格納する配列。 Noneが渡された場合は、新しい配列が割り当てられます。
- mode文字列、オプション
modeパラメータは、配列の境界をどのように処理するかを決定します。 有効なモードは、「max」、「min」、「ignore」です。 「max」または「ignore」の場合、画像ドメイン外のピクセルはTrueであると想定されるため、結果に影響を与えません。 デフォルトは「ignore」です。バージョン0.23で追加:
modeは0.23で追加されました。
- 戻り値:
- eroded真偽値またはuintのndarray
[False, True]の値を持つモルフォロジー的収縮の結果。
注記
フットプリントは、2タプルのシーケンスとして提供することもできます。各2タプルの最初の要素はフットプリントndarrayで、2番目の要素は反復する回数を表す整数です。 たとえば、
footprint=[(np.ones((9, 1)), 1), (np.ones((1, 9)), 1)]は、9x1フットプリントに続いて1x9フットプリントを適用します。その結果、footprint=np.ones((9, 9))と同じ効果が得られますが、計算コストは低くなります。skimage.morphology.disk()などの組み込みフットプリントのほとんどは、このタイプのフットプリントシーケンスを自動的に生成するオプションを提供します。偶数サイズのフットプリントの場合、
skimage.morphology.erosion()とこの関数は異なる出力を生成します。 一方は他方と比較して1ピクセルずれています。
- skimage.morphology.binary_opening(image, footprint=None, out=None, *, mode='ignore')[source]#
画像の高速なバイナリモルフォロジーオープニングを返します。
この関数は、グレースケール opening と同じ結果を返しますが、バイナリ画像に対してより高速に実行されます。
画像に対するモルフォロジー opening は、収縮後に膨張を行うことで定義されます。Opening は、小さな明るい点(つまり「塩」)を除去し、小さな暗い亀裂を接続することができます。これは、(明るい)特徴間の(暗い)ギャップを「開く」傾向があります。
- パラメータ:
- **image**: ndarray
バイナリ入力画像。
- footprintndarray または タプル、オプション
1と0の2次元配列として表される近傍。 Noneの場合、十字型のフットプリント(connectivity = 1)を使用します。 フットプリントは、以下の注記で説明されているように、より小さなフットプリントのシーケンスとして提供することもできます。
- out真偽値のndarray、オプション
モルフォロジーの結果を格納する配列。 Noneが渡された場合は、新しい配列が割り当てられます。
- mode文字列、オプション
modeパラメータは、配列の境界をどのように処理するかを決定します。 有効なモードは、「max」、「min」、「ignore」です。 「ignore」の場合、画像ドメイン外のピクセルは、収縮の場合はTrue、膨張の場合はFalseであると想定されるため、結果に影響を与えません。 デフォルトは「ignore」です。バージョン0.23で追加:
modeは0.23で追加されました。
- 戻り値:
- openingブール値のndarray
モルフォロジー opening の結果。
注記
フットプリントは、2タプルのシーケンスとして提供することもできます。各2タプルの最初の要素はフットプリントndarrayで、2番目の要素は反復する回数を表す整数です。 たとえば、
footprint=[(np.ones((9, 1)), 1), (np.ones((1, 9)), 1)]は、9x1フットプリントに続いて1x9フットプリントを適用します。その結果、footprint=np.ones((9, 9))と同じ効果が得られますが、計算コストは低くなります。skimage.morphology.disk()などの組み込みフットプリントのほとんどは、このタイプのフットプリントシーケンスを自動的に生成するオプションを提供します。
- skimage.morphology.black_tophat(image, footprint=None, out=None, *, mode='reflect', cval=0.0)[source]#
画像のブラックトップハットを返します。
画像のブラック トップハットは、そのモルフォロジー クロージングから元の画像を引いたものとして定義されます。この操作は、フットプリントよりも小さい画像の暗いスポットを返します。元の画像の暗いスポットは、ブラック トップハットの後には明るいスポットになることに注意してください。
- パラメータ:
- **image**: ndarray
画像配列。
- footprintndarray または タプル、オプション
1と0の2次元配列として表される近傍。 Noneの場合、十字型のフットプリント(connectivity = 1)を使用します。 フットプリントは、以下の注記で説明されているように、より小さなフットプリントのシーケンスとして提供することもできます。
- outndarray、オプション
モルフォロジーの結果を格納する配列。 Noneが渡された場合は、新しい配列が割り当てられます。
- mode文字列、オプション
modeパラメータは、配列の境界をどのように処理するかを決定します。有効なモードは、「reflect」、「constant」、「nearest」、「mirror」、「wrap」、「max」、「min」、または「ignore」です。skimage.morphology.closing()を参照してください。デフォルトは「reflect」です。- cvalスカラー、オプション
modeが「constant」の場合、入力のエッジを越えた部分を埋める値。デフォルトは 0.0 です。バージョン 0.23 で追加:
modeとcvalは 0.23 で追加されました。
- 戻り値:
- out
imageと同じ形状とタイプの配列 モルフォロジー ブラック トップハットの結果。
- out
参照
注記
フットプリントは、2タプルのシーケンスとして提供することもできます。各2タプルの最初の要素はフットプリントndarrayで、2番目の要素は反復する回数を表す整数です。 たとえば、
footprint=[(np.ones((9, 1)), 1), (np.ones((1, 9)), 1)]は、9x1フットプリントに続いて1x9フットプリントを適用します。その結果、footprint=np.ones((9, 9))と同じ効果が得られますが、計算コストは低くなります。skimage.morphology.disk()などの組み込みフットプリントのほとんどは、このタイプのフットプリントシーケンスを自動的に生成するオプションを提供します。参考文献
例
>>> # Change dark peak to bright peak and subtract background >>> import numpy as np >>> from skimage.morphology import footprint_rectangle >>> dark_on_gray = np.array([[7, 6, 6, 6, 7], ... [6, 5, 4, 5, 6], ... [6, 4, 0, 4, 6], ... [6, 5, 4, 5, 6], ... [7, 6, 6, 6, 7]], dtype=np.uint8) >>> black_tophat(dark_on_gray, footprint_rectangle((3, 3))) array([[0, 0, 0, 0, 0], [0, 0, 1, 0, 0], [0, 1, 5, 1, 0], [0, 0, 1, 0, 0], [0, 0, 0, 0, 0]], dtype=uint8)
- skimage.morphology.closing(image, footprint=None, out=None, *, mode='reflect', cval=0.0)[source]#
画像のグレースケールモルフォロジークロージングを返します。
画像のモルフォロジー クロージングは、膨張後に収縮を行うことで定義されます。クロージングは、小さな暗い点(つまり「胡椒」)を除去し、小さな明るい亀裂を接続することができます。これは、(明るい)特徴間の(暗い)ギャップを「閉じる」傾向があります。
- パラメータ:
- **image**: ndarray
画像配列。
- footprintndarray または タプル、オプション
1と0の2次元配列として表される近傍。 Noneの場合、十字型のフットプリント(connectivity = 1)を使用します。 フットプリントは、以下の注記で説明されているように、より小さなフットプリントのシーケンスとして提供することもできます。
- outndarray、オプション
モルフォロジーの結果を格納する配列。None の場合、新しい配列が割り当てられます。
- mode文字列、オプション
modeパラメータは、配列の境界をどのように処理するかを決定します。有効なモードは、「reflect」、「constant」、「nearest」、「mirror」、「wrap」、「max」、「min」、または「ignore」です。「ignore」の場合、画像領域外のピクセルは、収縮では画像のデータ型の最大値、膨張では最小値と見なされ、結果に影響を与えません。デフォルトは「reflect」です。- cvalスカラー、オプション
modeが「constant」の場合、入力のエッジを越えた部分を埋める値。デフォルトは 0.0 です。バージョン 0.23 で追加:
modeとcvalは 0.23 で追加されました。
- 戻り値:
- closing
imageと同じ形状とタイプの配列 モルフォロジー的クロージングの結果。
- closing
注記
フットプリントは、2タプルのシーケンスとして提供することもできます。各2タプルの最初の要素はフットプリントndarrayで、2番目の要素は反復する回数を表す整数です。 たとえば、
footprint=[(np.ones((9, 1)), 1), (np.ones((1, 9)), 1)]は、9x1フットプリントに続いて1x9フットプリントを適用します。その結果、footprint=np.ones((9, 9))と同じ効果が得られますが、計算コストは低くなります。skimage.morphology.disk()などの組み込みフットプリントのほとんどは、このタイプのフットプリントシーケンスを自動的に生成するオプションを提供します。例
>>> # Close a gap between two bright lines >>> import numpy as np >>> from skimage.morphology import footprint_rectangle >>> broken_line = np.array([[0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0], ... [1, 1, 0, 1, 1], ... [0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0]], dtype=np.uint8) >>> closing(broken_line, footprint_rectangle((3, 3))) array([[0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [1, 1, 1, 1, 1], [0, 0, 0, 0, 0], [0, 0, 0, 0, 0]], dtype=uint8)
- skimage.morphology.convex_hull_image(image, offset_coordinates=True, tolerance=1e-10, include_borders=True)[source]#
バイナリ画像の凸包画像を計算します。
凸包とは、入力画像内のすべての白いピクセルを囲む最小の凸多角形に含まれるピクセルの集合です。
- パラメータ:
- image配列
バイナリ入力画像。この配列は処理前にブール値にキャストされます。
- offset_coordinatesブール値、オプション
Trueの場合、たとえば (4, 7) の座標にあるピクセルは、座標 (3.5, 7)、(4.5, 7)、(4, 6.5)、および (4, 7.5) で表されます。これは、凸包を計算するときにピクセルに「範囲」を追加します。- tolerance浮動小数点数、オプション
点が凸包内にあるかどうかを判断する際の許容誤差。数値的な浮動小数点誤差のため、許容誤差が 0 の場合、一部の点が誤って凸包外として分類される可能性があります。
- include_borders: ブール値、オプション
Falseの場合、頂点/エッジは最終的な凸包マスクから除外されます。
- 戻り値:
- hull(M, N) ブール値の配列
凸包内のピクセルが True に設定されたバイナリ画像。
参考文献
- skimage.morphology.convex_hull_object(image, *, connectivity=2)[source]#
バイナリ画像内の個々のオブジェクトの凸包画像を計算します。
凸包とは、入力画像内のすべての白いピクセルを囲む最小の凸多角形に含まれるピクセルの集合です。
- パラメータ:
- image(M, N) ndarray
バイナリ入力画像。
- connectivity{1, 2}、整数、オプション
各ピクセルの近傍を決定します。ピクセルの中心から
connectivityの二乗距離内にある隣接要素は、近傍と見なされます。1-connectivity 2-connectivity [ ] [ ] [ ] [ ] | \ | / [ ]--[x]--[ ] [ ]--[x]--[ ] | / | \ [ ] [ ] [ ] [ ]
- 戻り値:
- hullブール値のndarray
凸包内のピクセルが
Trueに設定されたバイナリ画像。
注記
この関数は、
skimage.morphology.labelを使用して一意のオブジェクトを定義し、convex_hull_imageを使用してそれぞれの凸包を見つけ、これらの領域を論理 OR で結合します。接続されていないオブジェクトの凸包が結果で重複する可能性があることに注意してください。これが疑われる場合は、各オブジェクトで convex_hull_image を個別に使用するか、connectivityを調整することを検討してください。
- skimage.morphology.diameter_closing(image, diameter_threshold=8, connectivity=1, parent=None, tree_traverser=None)[source]#
画像の直径クロージングを実行します。
直径クロージングは、最大拡張が diameter_threshold より小さい画像のすべての暗い構造を除去します。最大拡張は、バウンディングボックスの最大拡張として定義されます。この演算子は、バウンディングボックス クロージングとも呼ばれます。実際には、結果はモルフォロジークロージングに似ていますが、長くて細い構造は削除されません。
技術的には、この演算子は画像の最大ツリー表現に基づいています。
- パラメータ:
- **image**: ndarray
直径クロージングを計算する入力画像。この画像は任意のタイプにすることができます。
- diameter_threshold符号なし整数
最大拡張パラメータ(ピクセル数)。デフォルト値は 8 です。
- **connectivity**: 符号なし整数、オプション
近傍接続性。整数は、隣接に到達するための直交ステップの最大数を表します。2Dでは、4近傍の場合は1、8近傍の場合は2です。デフォルト値は1です。
- **parent**: ndarray、int64、オプション
反転画像の最大ツリーを表す、事前に計算された親画像。事前に計算された parent と tree_traverser が提供されている場合、この関数は高速です。詳細については、注記を参照してください。
- **tree_traverser**: 1D配列、int64、オプション
事前に計算されたトラバーサー。ピクセルは、すべてのピクセルがその親の前に配置されるように順序付けられます(親のないルートを除く)。事前に計算された parent と tree_traverser が提供されている場合、この関数は高速です。詳細については、注記を参照してください。
- 戻り値:
- **output**: ndarray
入力画像と同じ形状と型の出力画像。
参照
注記
最大ツリー表現(parentとtree_traverser)が関数に与えられる場合、この関数の反転画像から計算する必要があります。つまり、>>> P, S = max_tree(invert(f)) >>> closed = diameter_closing(f, 3, parent=P, tree_traverser=S)
参考文献
[1]Walter, T. & Klein, J.-C. (2002). バウンディングボックスクロージングを用いたヒト網膜カラー眼底画像における微小動脈瘤の自動検出. Colosimo, A., Sirabella, P., Giuliani, A. (編), Medical Data Analysis. Lecture Notes in Computer Science, vol 2526, pp. 210-220. Springer Berlin Heidelberg. DOI:10.1007/3-540-36104-9_23
[2]Carlinet, E., & Geraud, T. (2014). A Comparative Review of Component Tree Computation Algorithms. IEEE Transactions on Image Processing, 23(9), 3885-3895. DOI:10.1109/TIP.2014.2336551
例
画像を作成します(中心に最小値、さらに4つの局所的最小値を持つ二次関数)。
>>> w = 12 >>> x, y = np.mgrid[0:w,0:w] >>> f = 180 + 0.2*((x - w/2)**2 + (y-w/2)**2) >>> f[2:3,1:5] = 160; f[2:4,9:11] = 140; f[9:11,2:4] = 120 >>> f[9:10,9:11] = 100; f[10,10] = 100 >>> f = f.astype(int)
直径クロージングを計算することができます。
>>> closed = diameter_closing(f, 3, connectivity=1)
最大拡張が2以下のすべての小さな極小値が削除されます。残りの極小値はすべて、少なくとも3の最大拡張を持ちます。
- skimage.morphology.diameter_opening(image, diameter_threshold=8, connectivity=1, parent=None, tree_traverser=None)[source]#
画像の直径オープニングを実行します。
直径オープニングは、最大拡張がdiameter_thresholdより小さい画像のすべての明るい構造を削除します。最大拡張は、バウンディングボックスの最大拡張として定義されます。この演算子は、バウンディングボックスオープニングとも呼ばれます。実際には、結果はモルフォロジーオープニングに似ていますが、細長い構造は削除されません。
技術的には、この演算子は画像の最大ツリー表現に基づいています。
- パラメータ:
- **image**: ndarray
area_opening を計算する入力画像。この画像は任意の型にすることができます。
- diameter_threshold符号なし整数
最大拡張パラメータ(ピクセル数)。デフォルト値は 8 です。
- **connectivity**: 符号なし整数、オプション
近傍接続性。整数は、隣接に到達するための直交ステップの最大数を表します。2Dでは、4近傍の場合は1、8近傍の場合は2です。デフォルト値は1です。
- **parent**: ndarray、int64、オプション
画像の最大ツリーを表す親画像。各ピクセルの値は、ravelled配列における親のインデックスです。
- **tree_traverser**: 1D配列、int64、オプション
順序付けられたピクセルインデックス(ravelled配列を参照)。ピクセルは、すべてのピクセルがその親の前に来るように順序付けられます(親のないルートを除く)。
- 戻り値:
- **output**: ndarray
入力画像と同じ形状と型の出力画像。
参照
参考文献
[1]Walter, T. & Klein, J.-C. (2002). バウンディングボックスクロージングを用いたヒト網膜カラー眼底画像における微小動脈瘤の自動検出. Colosimo, A., Sirabella, P., Giuliani, A. (編), Medical Data Analysis. Lecture Notes in Computer Science, vol 2526, pp. 210-220. Springer Berlin Heidelberg. DOI:10.1007/3-540-36104-9_23
[2]Carlinet, E., & Geraud, T. (2014). A Comparative Review of Component Tree Computation Algorithms. IEEE Transactions on Image Processing, 23(9), 3885-3895. DOI:10.1109/TIP.2014.2336551
例
画像を作成します(中心に最大値、さらに4つの局所的最大値を持つ二次関数)。
>>> w = 12 >>> x, y = np.mgrid[0:w,0:w] >>> f = 20 - 0.2*((x - w/2)**2 + (y-w/2)**2) >>> f[2:3,1:5] = 40; f[2:4,9:11] = 60; f[9:11,2:4] = 80 >>> f[9:10,9:11] = 100; f[10,10] = 100 >>> f = f.astype(int)
直径オープニングを計算することができます。
>>> open = diameter_opening(f, 3, connectivity=1)
最大拡張が2以下のピークが削除されます。残りのピークはすべて、少なくとも3の最大拡張を持ちます。
- skimage.morphology.diamond(radius, dtype=<class 'numpy.uint8'>, *, decomposition=None)[source]#
平坦なダイヤモンド型のフットプリントを生成します。
ピクセルは、それ自体と近傍の中心との間のシティブロック/マンハッタン距離がradius以下である場合、近傍の一部(つまり、1とラベル付けされた)です。
- パラメータ:
- radiusint
ひし形フットプリントの半径。
- 戻り値:
- footprintndarray または タプル
近傍の要素が1で、それ以外の場合は0であるフットプリント。`decomposition`がNoneの場合、これは単なるnumpy.ndarrayです。それ以外の場合、これは適用する一意の構造化要素の数に等しい長さのタプルになります(詳細については注記を参照)。
- その他の引数:
- dtypeデータ型、オプション
フットプリントのデータ型。
- decomposition{None, 'sequence'}、オプション
Noneの場合、単一の配列が返されます。「sequence」の場合、より小さなフットプリントのタプルが返されます。この一連の小さなフットプリントを適用すると、単一の大きなフットプリントと同じ結果が得られますが、計算パフォーマンスが向上します。詳細については、注記を参照してください。
注記
`decomposition`がNoneでない場合、`footprint`タプルの各要素は、フットプリント配列とそれが適用される反復回数を指定する`(ndarray、num_iter)`形式の2タプルです。
バイナリまたはグレースケールのモルフォロジーのいずれの場合でも、`decomposition='sequence'`を使用すると、パフォーマンス上の利点があり、フットプリントサイズが大きくなるほど利点の大きさが増すことが観察されました。
- skimage.morphology.dilation(image, footprint=None, out=None, shift_x=<DEPRECATED>, shift_y=<DEPRECATED>, *, mode='reflect', cval=0.0)[source]#
画像のグレースケールモルフォロジー膨張を返します。
モルフォロジーダイレーションは、ピクセルの値を、それを中心とする局所近傍内のすべてのピクセル値の最大値に設定します。フットプリントが1である値がこの近傍を定義します。ダイレーションは明るい領域を拡大し、暗い領域を縮小します。
- パラメータ:
- **image**: ndarray
画像配列。
- footprintndarray または タプル、オプション
1と0の2次元配列として表される近傍。 Noneの場合、十字型のフットプリント(connectivity = 1)を使用します。 フットプリントは、以下の注記で説明されているように、より小さなフットプリントのシーケンスとして提供することもできます。
- outndarray、オプション
モルフォロジーの結果を格納する配列。 Noneが渡された場合は、新しい配列が割り当てられます。
- mode文字列、オプション
`mode`パラメータは、配列の境界をどのように処理するかを決定します。有効なモードは、「reflect」、「constant」、「nearest」、「mirror」、「wrap」、「max」、「min」、または「ignore」です。「min」または「ignore」の場合、画像領域外のピクセルは画像のdtypeの最大値であると見なされ、結果に影響を与えません。デフォルトは「reflect」です。
- cvalスカラー、オプション
modeが「constant」の場合、入力のエッジを越えた部分を埋める値。デフォルトは 0.0 です。バージョン 0.23 で追加:
modeとcvalは 0.23 で追加されました。
- 戻り値:
- dilateduint8 array, `image`と同じ形状とタイプ
モルフォロジーダイレーションの結果。
- その他の引数:
- shift_x, shift_y非推奨
バージョン0.23以降非推奨です。
注記
`uint8`(および特定のビット深度までの`uint16`)データの場合、アルゴリズムの複雑さが低いほど、大きな画像やフットプリントに対して
skimage.filters.rank.maximum()関数がより効率的になります。フットプリントは、2タプルのシーケンスとして提供することもできます。各2タプルの最初の要素はフットプリントndarrayで、2番目の要素は反復する回数を表す整数です。 たとえば、
footprint=[(np.ones((9, 1)), 1), (np.ones((1, 9)), 1)]は、9x1フットプリントに続いて1x9フットプリントを適用します。その結果、footprint=np.ones((9, 9))と同じ効果が得られますが、計算コストは低くなります。skimage.morphology.disk()などの組み込みフットプリントのほとんどは、このタイプのフットプリントシーケンスを自動的に生成するオプションを提供します。非対称フットプリントの場合、
skimage.morphology.binary_dilation()とskimage.morphology.dilation()は異なる出力を生成します。binary_dilationはフットプリントをミラーリングしますが、dilationはミラーリングしません。例
>>> # Dilation enlarges bright regions >>> import numpy as np >>> from skimage.morphology import footprint_rectangle >>> bright_pixel = np.array([[0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0], ... [0, 0, 1, 0, 0], ... [0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0]], dtype=np.uint8) >>> dilation(bright_pixel, footprint_rectangle((3, 3))) array([[0, 0, 0, 0, 0], [0, 1, 1, 1, 0], [0, 1, 1, 1, 0], [0, 1, 1, 1, 0], [0, 0, 0, 0, 0]], dtype=uint8)
- skimage.morphology.disk(radius, dtype=<class 'numpy.uint8'>, *, strict_radius=True, decomposition=None)[source]#
平坦な円盤型のフットプリントを生成します。
ピクセルは、それ自体と原点との間のユークリッド距離がradius以下の場合、近傍内にあります(これは、`decomposition == 'sequence'`の場合、おおよそ真です)。
- パラメータ:
- radiusint
円形フットプリントの半径。
- 戻り値:
- footprintndarray
近傍の要素が1、それ以外の要素が0であるフットプリント。
- その他の引数:
- dtypeデータ型、オプション
フットプリントのデータ型。
- strict_radius真偽値、オプション
Falseの場合、半径を0.5拡張します。これにより、円は、各軸に沿ってサイズが
2 * radius + 1のままである立方体内をさらに拡張できます。 decomposition が None でない場合、このパラメータは無視されます。- decomposition{None, ‘sequence’, ‘crosses’}, optional
Noneの場合、単一の配列が返されます。「sequence」の場合、より小さなフットプリントのタプルが返されます。この一連の小さなフットプリントを適用すると、単一の大きなフットプリントと同じ結果が得られますが、計算パフォーマンスが向上します。ディスクフットプリントの場合、「sequence」または「crosses」分解は、必ずしも`decomposition=None`と完全に同等ではありません。詳細については、注記を参照してください。
注記
`decomposition`がNoneでない場合、`footprint`タプルの各要素は、フットプリント配列とそれが適用される反復回数を指定する`(ndarray、num_iter)`形式の2タプルです。
`decomposition='sequence'`モードで生成されるディスクは、`decomposition=None`のディスクと同一ではない場合があります。ディスクフットプリントは、各軸に沿って範囲3のより小さなフットプリントのシリーズを適用することによって近似できます。これに対する具体的な解決策は、半径2〜10の2Dディスクの場合について[1]に示されています。ここでは、kwargs `strict_radius=False, decomposition=None`で計算されたディスクに最も近い一致を与える各要素の反復回数を数値的に計算しました。
経験的に、大きな半径での級数分解は、十六角形(16面の多角形[2])に近づきます。[3]では、著者は、形状(3、3)のフットプリントによる分解で実現できるディスクに最も近い近似は十六角形であることを示しています。
`decomposition='crosses'`によって生成されるディスクは、`decomposition=None`のディスクと同一である場合と同一でない場合がありますが、`decomposition='sequence'`よりも近い近似を与える傾向があり、パフォーマンスはかなり同等です。個々の十字形の要素のサイズは、範囲(3、3)に限定されません。「seqeuence」分解とは異なり、「crosses」分解は、`strict_radius=True`のディスクの形状も正確に近似できます。この方法は、[4]に示されているアルゴリズム1の適応に基づいています。
参考文献
[1]Park, H and Chin R.T. Decomposition of structuring elements for optimal implementation of morphological operations. In Proceedings: 1997 IEEE Workshop on Nonlinear Signal and Image Processing, London, UK. https://www.iwaenc.org/proceedings/1997/nsip97/pdf/scan/ns970226.pdf
[3]Vanrell, M and Vitrià, J. モルフォロジー変換のための最適な3×3分解可能ディスク。Image and Vision Computing、Vol.15、Issue 11、1997。 DOI:10.1016/S0262-8856(97)00026-7
[4]Li, D. and Ritter, G.X. 分離可能で対称な凸テンプレートの分解。Proc。SPIE 1350、Image Algebra and Morphological Image Processing、(1990年11月1日)。 DOI:10.1117/12.23608
- skimage.morphology.ellipse(width, height, dtype=<class 'numpy.uint8'>, *, decomposition=None)[source]#
平坦な楕円形のフットプリントを生成します。
楕円形の周囲にあるすべてのピクセルは、方程式
(x/width+1)**2 + (y/height+1)**2 = 1を満たします。- パラメータ:
- widthint
楕円形のフットプリントの幅。
- heightint
楕円形のフットプリントの高さ。
- 戻り値:
- footprintndarray
近傍の要素が1で、それ以外は0であるフットプリント。フットプリントの形状は
(2 * height + 1, 2 * width + 1)になります。
- その他の引数:
- dtypeデータ型、オプション
フットプリントのデータ型。
- decomposition{None, ‘crosses’}, optional
Noneの場合、単一の配列が返されます。「sequence」の場合、より小さなフットプリントのタプルが返されます。この一連の小さなフットプリントを適用すると、単一の大きなフットプリントと同じ結果が得られますが、計算パフォーマンスが向上します。詳細については、注記を参照してください。
注記
`decomposition`がNoneでない場合、`footprint`タプルの各要素は、フットプリント配列とそれが適用される反復回数を指定する`(ndarray、num_iter)`形式の2タプルです。
decomposition='crosses'によって生成される楕円は、decomposition=Noneの場合としばしば同じになりますが、常に同じになるとは限りません。このメソッドは、[1] に示されているアルゴリズム1の適応に基づいています。参考文献
[1]Li, D. and Ritter, G.X. 分離可能で対称な凸テンプレートの分解。Proc。SPIE 1350、Image Algebra and Morphological Image Processing、(1990年11月1日)。 DOI:10.1117/12.23608
例
>>> from skimage.morphology import footprints >>> footprints.ellipse(5, 3) array([[0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0]], dtype=uint8)
- skimage.morphology.erosion(image, footprint=None, out=None, shift_x=<DEPRECATED>, shift_y=<DEPRECATED>, *, mode='reflect', cval=0.0)[source]#
画像のグレースケールモルフォロジー収縮を返します。
モルフォロジーエロージョンは、(i,j) におけるピクセルを、(i,j) を中心とする近傍のすべてのピクセルの最小値に設定します。エロージョンは明るい領域を縮小し、暗い領域を拡大します。
- パラメータ:
- **image**: ndarray
画像配列。
- footprintndarray または タプル、オプション
1と0の2次元配列として表される近傍。 Noneの場合、十字型のフットプリント(connectivity = 1)を使用します。 フットプリントは、以下の注記で説明されているように、より小さなフットプリントのシーケンスとして提供することもできます。
- outndarray, optional
モルフォロジーの結果を格納する配列。 Noneが渡された場合は、新しい配列が割り当てられます。
- mode文字列、オプション
modeパラメータは、配列の境界をどのように処理するかを決定します。有効なモードは、'reflect'、'constant'、'nearest'、'mirror'、'wrap'、'max'、'min'、または 'ignore' です。'max' または 'ignore' の場合、画像領域外のピクセルは画像の dtype の最大値と見なされ、結果に影響を与えません。デフォルトは 'reflect' です。- cvalスカラー、オプション
modeが「constant」の場合、入力のエッジを越えた部分を埋める値。デフォルトは 0.0 です。バージョン 0.23 で追加:
modeとcvalは 0.23 で追加されました。
- 戻り値:
- erodedarray,
imageと同じ形状 モルフォロジーエロージョンの結果。
- erodedarray,
- その他の引数:
- shift_x, shift_y非推奨
バージョン0.23以降非推奨です。
注記
uint8(および特定のビット深度までのuint16)データの場合、アルゴリズムの複雑さが低いため、大きな画像やフットプリントに対してskimage.filters.rank.minimum()関数の方が効率的です。フットプリントは、2タプルのシーケンスとして提供することもできます。各2タプルの最初の要素はフットプリントndarrayで、2番目の要素は反復する回数を表す整数です。 たとえば、
footprint=[(np.ones((9, 1)), 1), (np.ones((1, 9)), 1)]は、9x1フットプリントに続いて1x9フットプリントを適用します。その結果、footprint=np.ones((9, 9))と同じ効果が得られますが、計算コストは低くなります。skimage.morphology.disk()などの組み込みフットプリントのほとんどは、このタイプのフットプリントシーケンスを自動的に生成するオプションを提供します。偶数サイズのフットプリントの場合、
skimage.morphology.binary_erosion()とこの関数は、異なる出力を生成します。一方は他方と比較して1ピクセルずれています。例
>>> # Erosion shrinks bright regions >>> import numpy as np >>> from skimage.morphology import footprint_rectangle >>> bright_square = np.array([[0, 0, 0, 0, 0], ... [0, 1, 1, 1, 0], ... [0, 1, 1, 1, 0], ... [0, 1, 1, 1, 0], ... [0, 0, 0, 0, 0]], dtype=np.uint8) >>> erosion(bright_square, footprint_rectangle((3, 3))) array([[0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [0, 0, 1, 0, 0], [0, 0, 0, 0, 0], [0, 0, 0, 0, 0]], dtype=uint8)
- skimage.morphology.flood(image, seed_point, *, footprint=None, connectivity=None, tolerance=None)[source]#
フラッドフィルに対応するマスク。
特定の
seed_pointから開始して、シード値と等しいか、tolerance内にある連結された点を見つけます。- パラメータ:
- **image**: ndarray
n次元配列。
- seed_pointタプルまたは整数
フラッドフィルの開始点として使用される
image内の点。画像が1Dの場合、この点は整数として指定できます。- footprintndarray、オプション
各評価ピクセルの近傍を決定するために使用されるフットプリント(構造化要素)。1と0のみを含み、
imageと同じ次元数である必要があります。指定しない場合、すべての隣接ピクセルは近傍の一部と見なされます(完全連結)。- connectivityint、オプション
各評価ピクセルの近傍を決定するために使用される数値。中心からの二乗距離が
connectivity以下の隣接ピクセルは、近傍と見なされます。footprintが None でない場合は無視されます。- tolerancefloat または int、オプション
None(デフォルト)の場合、隣接値は
seed_pointにおけるimageの初期値と厳密に等しくなければなりません。これは最速です。値が指定されている場合、すべての点で比較が行われ、初期値の許容範囲内であれば塗りつぶされます(包括的)。
- 戻り値:
- maskndarray
imageと同じ形状のブール値配列が返されます。シードポイントに接続され、等しい(または許容範囲内)領域は True 値になります。他のすべての値は False です。
注記
この操作の概念的なアナロジーは、多くのラスターグラフィックプログラムの「ペイントバケット」ツールです。この関数は、塗りつぶしを表すマスクのみを返します。
メモリの理由からマスクではなくインデックスが必要な場合は、結果に対して
numpy.nonzeroを実行し、インデックスを保存して、このマスクを破棄するだけです。例
>>> from skimage.morphology import flood >>> image = np.zeros((4, 7), dtype=int) >>> image[1:3, 1:3] = 1 >>> image[3, 0] = 1 >>> image[1:3, 4:6] = 2 >>> image[3, 6] = 3 >>> image array([[0, 0, 0, 0, 0, 0, 0], [0, 1, 1, 0, 2, 2, 0], [0, 1, 1, 0, 2, 2, 0], [1, 0, 0, 0, 0, 0, 3]])
完全な連結性(対角線を含む)で、連結された1を5で塗りつぶします
>>> mask = flood(image, (1, 1)) >>> image_flooded = image.copy() >>> image_flooded[mask] = 5 >>> image_flooded array([[0, 0, 0, 0, 0, 0, 0], [0, 5, 5, 0, 2, 2, 0], [0, 5, 5, 0, 2, 2, 0], [5, 0, 0, 0, 0, 0, 3]])
対角点(連結性1)を除外して、連結された1を5で塗りつぶします
>>> mask = flood(image, (1, 1), connectivity=1) >>> image_flooded = image.copy() >>> image_flooded[mask] = 5 >>> image_flooded array([[0, 0, 0, 0, 0, 0, 0], [0, 5, 5, 0, 2, 2, 0], [0, 5, 5, 0, 2, 2, 0], [1, 0, 0, 0, 0, 0, 3]])
許容範囲を指定して塗りつぶします
>>> mask = flood(image, (0, 0), tolerance=1) >>> image_flooded = image.copy() >>> image_flooded[mask] = 5 >>> image_flooded array([[5, 5, 5, 5, 5, 5, 5], [5, 5, 5, 5, 2, 2, 5], [5, 5, 5, 5, 2, 2, 5], [5, 5, 5, 5, 5, 5, 3]])
- skimage.morphology.flood_fill(image, seed_point, new_value, *, footprint=None, connectivity=None, tolerance=None, in_place=False)[source]#
画像にフラッドフィルを実行します。
特定の
seed_pointから開始して、シード値と等しいか、tolerance内にある連結された点を見つけ、new_valueに設定します。- パラメータ:
- **image**: ndarray
n次元配列。
- seed_pointタプルまたは整数
フラッドフィルの開始点として使用される
image内の点。画像が1Dの場合、この点は整数として指定できます。- new_value
imageタイプ 塗りつぶし全体に設定する新しい値。これは
imageのデータ型と一致するように選択する必要があります。- footprintndarray、オプション
各評価ピクセルの近傍を決定するために使用されるフットプリント(構造化要素)。1と0のみを含み、
imageと同じ次元数である必要があります。指定しない場合、すべての隣接ピクセルは近傍の一部と見なされます(完全連結)。- connectivityint、オプション
各評価ピクセルの近傍を決定するために使用される数値。中心からの二乗距離が
connectivity以下の隣接ピクセルは、近傍と見なされます。footprintが None でない場合は無視されます。- tolerancefloat または int、オプション
None(デフォルト)の場合、隣接値は塗りつぶされる
seed_pointにおけるimageの値と厳密に等しくなければなりません。これは最速です。許容範囲が指定されている場合、シードポイントからプラスマイナス許容範囲内の値を持つ隣接点が塗りつぶされます(包括的)。- in_placebool、オプション
True の場合、フラッドフィルは
imageに直接適用されます。False の場合、フラッドフィルされた結果が入力imageを変更せずに返されます(デフォルト)。
- 戻り値:
- filledndarray
imageと同じ形状の配列が返されます。シードポイントに接続され、等しい(または許容範囲内)領域の値はnew_valueに置き換えられます。
注記
この操作の概念的なアナロジーは、多くのラスターグラフィックプログラムの「ペイントバケット」ツールです。
例
>>> from skimage.morphology import flood_fill >>> image = np.zeros((4, 7), dtype=int) >>> image[1:3, 1:3] = 1 >>> image[3, 0] = 1 >>> image[1:3, 4:6] = 2 >>> image[3, 6] = 3 >>> image array([[0, 0, 0, 0, 0, 0, 0], [0, 1, 1, 0, 2, 2, 0], [0, 1, 1, 0, 2, 2, 0], [1, 0, 0, 0, 0, 0, 3]])
完全な連結性(対角線を含む)で、連結された1を5で塗りつぶします
>>> flood_fill(image, (1, 1), 5) array([[0, 0, 0, 0, 0, 0, 0], [0, 5, 5, 0, 2, 2, 0], [0, 5, 5, 0, 2, 2, 0], [5, 0, 0, 0, 0, 0, 3]])
対角点(連結性1)を除外して、連結された1を5で塗りつぶします
>>> flood_fill(image, (1, 1), 5, connectivity=1) array([[0, 0, 0, 0, 0, 0, 0], [0, 5, 5, 0, 2, 2, 0], [0, 5, 5, 0, 2, 2, 0], [1, 0, 0, 0, 0, 0, 3]])
許容範囲を指定して塗りつぶします
>>> flood_fill(image, (0, 0), 5, tolerance=1) array([[5, 5, 5, 5, 5, 5, 5], [5, 5, 5, 5, 2, 2, 5], [5, 5, 5, 5, 2, 2, 5], [5, 5, 5, 5, 5, 5, 3]])
- skimage.morphology.footprint_from_sequence(footprints)[source]#
フットプリントシーケンスを等価なndarrayに変換します。
- パラメータ:
- **footprints**2要素タプルのタプル
フットプリントタプルのシーケンス。各タプルの最初の要素はフットプリントに対応する配列で、2番目の要素は適用回数です。現在、すべてのフットプリントは奇数サイズである必要があります。
- 戻り値:
- footprintndarray
footprintsのシーケンスを適用することと同等の単一の配列。
- skimage.morphology.footprint_rectangle(shape, *, dtype=<class 'numpy.uint8'>, decomposition=None)[source]#
矩形または超矩形のフットプリントを生成します。
`shape`で指定された長さおよび次元に応じて、正方形、長方形、立方体、直方体、またはさらに高次元の形状を生成します。
- パラメータ:
- shapetuple[int, …]
各次元におけるフットプリントの長さ。シーケンスの長さは、フットプリントの次元数を決定します。
- dtypeデータ型、オプション
フットプリントのデータ型。
- decomposition{None, ‘separable’, ‘sequence’}, optional
Noneの場合、単一の配列が返されます。「sequence」の場合、より小さなフットプリントのタプルが返されます。この一連の小さなフットプリントを適用すると、単一の大きなフットプリントと同じ結果が得られますが、多くの場合、計算パフォーマンスが向上します。詳細は注意事項を参照してください。「separable」の場合、この関数は各軸に個別分離可能な1Dフットプリントを使用します。「sequence」と「separable」のどちらの計算が高速かは、アーキテクチャによって異なる場合があります。
- 戻り値:
- footprintarray or tuple[tuple[ndarray, int], …]
1のみで構成されるフットプリント、つまりすべてのピクセルが近傍に属します。`decomposition`がNoneの場合、これは単なる配列です。それ以外の場合、これは適用する一意の構造化要素の数に等しい長さのタプルになります(詳細は例を参照)。
例
>>> import skimage as ski >>> ski.morphology.footprint_rectangle((3, 5)) array([[1, 1, 1, 1, 1], [1, 1, 1, 1, 1], [1, 1, 1, 1, 1]], dtype=uint8)
分解は、要求された形状の単純なフットプリントに結合する複数のフットプリントを返します。
>>> ski.morphology.footprint_rectangle((9, 9), decomposition="sequence") ((array([[1, 1, 1], [1, 1, 1], [1, 1, 1]], dtype=uint8), 4),)
`"sequence"`は、分解が1Dフットプリントのみを返すようにします。
>>> ski.morphology.footprint_rectangle((3, 5), decomposition="separable") ((array([[1], [1], [1]], dtype=uint8), 1), (array([[1, 1, 1, 1, 1]], dtype=uint8), 1))
各次元に3つのサンプルを持つ5次元ハイパーキューブを生成します
>>> ski.morphology.footprint_rectangle((3,) * 5).shape (3, 3, 3, 3, 3)
- skimage.morphology.h_maxima(image, h, footprint=None)[source]#
高さ>= hの画像のすべての極大値を決定します。
局所的最大値は、セットの直接近傍にあるすべてのピクセルのグレースケールレベルよりも厳密に大きい、等しいグレースケールレベルのピクセルの連結セットとして定義されます。
高さhの局所的最大値Mは、最小値がf(M)-hであるMと等しいかそれ以上の局所的最大値を結合するパスが少なくとも1つ存在する局所的最大値です(つまり、パスに沿った値は最大値に対してhを超えて減少していません)、最小値がそれ以上である、等しいかそれ以上の局所的最大値へのパスはありません。
画像のグローバルな最大値もこの関数で見つかります。
- パラメータ:
- **image**: ndarray
最大値を計算する入力画像。
- h符号なし整数
抽出されたすべての最大値の最小の高さ。
- footprintndarray、オプション
1と0のn次元配列として表される近傍。デフォルトは、最大ノルムに従って半径1の球です(つまり、2D画像の場合は3x3の正方形、3D画像の場合は3x3x3の立方体など)。
- 戻り値:
- h_maxndarray
高さ>= hの局所的最大値とグローバルな最大値。結果の画像はバイナリ画像であり、決定された最大値に属するピクセルは値1を取り、他のピクセルは値0を取ります。
参考文献
[1]Soille、P.、「形態画像分析:原則と応用」(第6章)、第2版(2003)、ISBN 3540429883。
例
>>> import numpy as np >>> from skimage.morphology import extrema
画像を作成します(中央に最大値があり、4つの追加の一定の最大値を持つ二次関数)。最大値の高さは、1、21、41、61、81です。
>>> w = 10 >>> x, y = np.mgrid[0:w,0:w] >>> f = 20 - 0.2*((x - w/2)**2 + (y-w/2)**2) >>> f[2:4,2:4] = 40; f[2:4,7:9] = 60; f[7:9,2:4] = 80; f[7:9,7:9] = 100 >>> f = f.astype(int)
少なくとも40の高さですべての最大値を計算できます
>>> maxima = extrema.h_maxima(f, 40)
結果の画像には、3つの局所的最大値が含まれます。
- skimage.morphology.h_minima(image, h, footprint=None)[source]#
深さ>= hの画像のすべての極小値を決定します。
局所的最小値は、セットの直接近傍にあるすべてのピクセルのグレースケールレベルよりも厳密に小さい、等しいグレースケールレベルのピクセルの連結セットとして定義されます。
深さhの局所的最小値Mは、最大値がf(M)+ hであるMと等しいかそれ以下の局所的最小値を結合するパスが少なくとも1つ存在する局所的最小値です(つまり、パスに沿った値は、最小値に対してhを超えて増加していません)、最大値がそれ以下である、等しいかそれ以下の局所的最小値へのパスはありません。
画像のグローバルな最小値もこの関数で見つかります。
- パラメータ:
- **image**: ndarray
最小値を計算する入力画像。
- h符号なし整数
抽出されたすべての最小値の最小深度。
- footprintndarray、オプション
1と0のn次元配列として表される近傍。デフォルトは、最大ノルムに従って半径1の球です(つまり、2D画像の場合は3x3の正方形、3D画像の場合は3x3x3の立方体など)。
- 戻り値:
- h_minndarray
深さ>= hの局所的最小値とグローバルな最小値。結果の画像はバイナリ画像であり、決定された最小値に属するピクセルは値1を取り、他のピクセルは値0を取ります。
参考文献
[1]Soille、P.、「形態画像分析:原則と応用」(第6章)、第2版(2003)、ISBN 3540429883。
例
>>> import numpy as np >>> from skimage.morphology import extrema
画像を作成します(中央に最小値があり、4つの追加の一定の最大値を持つ二次関数)。最小値の深さは、1、21、41、61、81です。
>>> w = 10 >>> x, y = np.mgrid[0:w,0:w] >>> f = 180 + 0.2*((x - w/2)**2 + (y-w/2)**2) >>> f[2:4,2:4] = 160; f[2:4,7:9] = 140; f[7:9,2:4] = 120; f[7:9,7:9] = 100 >>> f = f.astype(int)
少なくとも40の深さで、すべての最小値を計算できます
>>> minima = extrema.h_minima(f, 40)
結果の画像には、3つの局所的最小値が含まれます。
- skimage.morphology.isotropic_closing(image, radius, out=None, spacing=None)[source]#
画像のバイナリモルフォロジークロージングを返します。
この関数は、バイナリの`skimage.morphology.binary_closing()`と同じ結果を返しますが、大きな円形の構造化要素に対してより高速に実行されます。これは、正確なユークリッド距離マップ[1]、[2]にしきい値を適用することによって機能します。実装はfunc:`scipy.ndimage.distance_transform_edt`に基づいています。
- パラメータ:
- **image**: ndarray
バイナリ入力画像。
- radius浮動小数点数
領域を閉じる半径。
- out真偽値のndarray、オプション
モルフォロジーの結果を格納する配列。 Noneが渡された場合は、新しい配列が割り当てられます。
- spacingfloat、またはfloatのシーケンス、オプション
各次元 entlang の要素の間隔。シーケンスの場合、入力の次元(軸の数)と同じ長さでなければなりません。単一の数値の場合、この値はすべての軸に使用されます。指定しない場合、単位のグリッド間隔が暗示されます。
- 戻り値:
- closedブールのndarray
モルフォロジー的クロージングの結果。
参考文献
- skimage.morphology.isotropic_dilation(image, radius, out=None, spacing=None)[source]#
画像のバイナリモルフォロジー膨張を返します。
この関数は、`skimage.morphology.binary_dilation()`と同じ結果を返しますが、大きな円形の構造化要素に対してより高速に実行されます。これは、反転画像[1]、[2]の正確なユークリッド距離マップにしきい値を適用することによって機能します。実装はfunc:`scipy.ndimage.distance_transform_edt`に基づいています。
- パラメータ:
- **image**: ndarray
バイナリ入力画像。
- radius浮動小数点数
領域を拡張する半径。
- out真偽値のndarray、オプション
モルフォロジーの結果を格納する配列。 Noneが渡された場合は、新しい配列が割り当てられます。
- spacingfloat、またはfloatのシーケンス、オプション
各次元 entlang の要素の間隔。シーケンスの場合、入力の次元(軸の数)と同じ長さでなければなりません。単一の数値の場合、この値はすべての軸に使用されます。指定しない場合、単位のグリッド間隔が暗示されます。
- 戻り値:
- dilatedブールのndarray
[False, True]の値を持つモルフォロジー的膨張の結果。
参考文献
- skimage.morphology.isotropic_erosion(image, radius, out=None, spacing=None)[source]#
画像のバイナリモルフォロジー収縮を返します。
この関数は、
skimage.morphology.binary_erosion()と同じ結果を返しますが、大きな円形の構造化要素に対してより高速に実行されます。これは、画像の正確なユークリッド距離マップ [1], [2] にしきい値を適用することで機能します。実装は func:scipy.ndimage.distance_transform_edtに基づいています。- パラメータ:
- **image**: ndarray
バイナリ入力画像。
- radius浮動小数点数
領域を侵食する半径。
- out真偽値のndarray、オプション
モルフォロジーの結果を格納する配列。None の場合、新しい配列が割り当てられます。
- spacingfloat、またはfloatのシーケンス、オプション
各次元 entlang の要素の間隔。シーケンスの場合、入力の次元(軸の数)と同じ長さでなければなりません。単一の数値の場合、この値はすべての軸に使用されます。指定しない場合、単位のグリッド間隔が暗示されます。
- 戻り値:
- erodedブール値のndarray
[False, True]の値を持つモルフォロジー的収縮の結果。
参考文献
- skimage.morphology.isotropic_opening(image, radius, out=None, spacing=None)[source]#
画像のバイナリモルフォロジーオープニングを返します。
この関数は、
skimage.morphology.binary_opening()と同じ結果を返しますが、大きな円形の構造化要素に対してより高速に実行されます。これは、正確なユークリッド距離マップ [1], [2] にしきい値を適用することで機能します。実装は func:scipy.ndimage.distance_transform_edtに基づいています。- パラメータ:
- **image**: ndarray
バイナリ入力画像。
- radius浮動小数点数
領域を開く際に使用する半径。
- out真偽値のndarray、オプション
モルフォロジーの結果を格納する配列。 Noneが渡された場合は、新しい配列が割り当てられます。
- spacingfloat、またはfloatのシーケンス、オプション
各次元 entlang の要素の間隔。シーケンスの場合、入力の次元(軸の数)と同じ長さでなければなりません。単一の数値の場合、この値はすべての軸に使用されます。指定しない場合、単位のグリッド間隔が暗示されます。
- 戻り値:
- openedブール値のndarray
モルフォロジー opening の結果。
参考文献
- skimage.morphology.label(label_image, background=None, return_num=False, connectivity=None)[source]#
整数配列の連結領域にラベルを付けます。
2つのピクセルは、隣接していて同じ値を持つ場合に接続されているとみなされます。2Dでは、1接続または2接続のいずれかの意味で隣接している可能性があります。この値は、ピクセル/ボクセルを隣接とみなすために考慮する直交ホップの最大数を指します。
1-connectivity 2-connectivity diagonal connection close-up [ ] [ ] [ ] [ ] [ ] | \ | / | <- hop 2 [ ]--[x]--[ ] [ ]--[x]--[ ] [x]--[ ] | / | \ hop 1 [ ] [ ] [ ] [ ]
- パラメータ:
- label_imageint型のndarray
ラベル付けする画像。
- backgroundint、オプション
この値を持つすべてのピクセルを背景ピクセルとみなし、0としてラベル付けします。デフォルトでは、値が0のピクセルは背景ピクセルとみなされます。
- return_numブール値、オプション
割り当てられたラベルの数を返すかどうか。
- connectivityint、オプション
ピクセル/ボクセルを隣接とみなすために考慮する直交ホップの最大数。受け入れられる値は1からinput.ndimまでの範囲です。
Noneの場合、input.ndimの完全な接続が使用されます。
- 戻り値:
- labelsint型のndarray
ラベル付けされた配列。接続されたすべての領域に同じ整数値が割り当てられます。
- numint、オプション
ラベルの数。これは最大のラベルインデックスと等しく、return_numが
Trueの場合にのみ返されます。
参考文献
[1]Christophe Fiorio and Jens Gustedt, “Two linear time Union-Find strategies for image processing”, Theoretical Computer Science 154 (1996), pp. 165-181.
[2]Kensheng Wu, Ekow Otoo and Arie Shoshani, “Optimizing connected component labeling algorithms”, Paper LBNL-56864, 2005, Lawrence Berkeley National Laboratory (University of California), http://repositories.cdlib.org/lbnl/LBNL-56864
例
>>> import numpy as np >>> x = np.eye(3).astype(int) >>> print(x) [[1 0 0] [0 1 0] [0 0 1]] >>> print(label(x, connectivity=1)) [[1 0 0] [0 2 0] [0 0 3]] >>> print(label(x, connectivity=2)) [[1 0 0] [0 1 0] [0 0 1]] >>> print(label(x, background=-1)) [[1 2 2] [2 1 2] [2 2 1]] >>> x = np.array([[1, 0, 0], ... [1, 1, 5], ... [0, 0, 0]]) >>> print(label(x)) [[1 0 0] [1 1 2] [0 0 0]]
- skimage.morphology.local_maxima(image, footprint=None, connectivity=None, indices=False, allow_borders=True)[source]#
n次元配列の局所的最大値を見つけます。
局所的最大値は、近傍のすべてのピクセルのグレイレベルよりも厳密に大きい、等しいグレイレベル(プラトー)を持つピクセルの連結集合として定義されます。
- パラメータ:
- **image**: ndarray
n次元配列。
- footprintndarray、オプション
各評価ピクセルの近傍を決定するために使用されるフットプリント(構造化要素)(
Trueは接続されたピクセルを示します)。これはブール値の配列でなければならず、imageと同じ次元数を持たなければなりません。footprintもconnectivityも指定されていない場合、すべての隣接ピクセルが近傍の一部とみなされます。- connectivityint、オプション
各評価ピクセルの近傍を決定するために使用される数値。中心からの二乗距離が
connectivity以下の隣接ピクセルは、近傍と見なされます。footprintが None でない場合は無視されます。- indicesブール値、オプション
Trueの場合、出力は各次元における局所的最大値のインデックスを表す1次元配列のタプルになります。Falseの場合、出力は
imageと同じ形状を持つブール値の配列になります。- allow_bordersブール値、オプション
trueの場合、画像の境界線に接するプラトーは有効な最大値となります。
- 戻り値:
- maximandarray または tuple[ndarray]
indicesがfalseの場合、imageと同じ形状を持つブール値の配列が返され、Trueは局所的最大値の位置を示します(それ以外の場合はFalse)。indicesがtrueの場合、見つかったすべての最大値の座標(インデックス)を含む1次元配列のタプルが返されます。
- 警告:
- UserWarning
allow_bordersがfalseで、指定されたimageの次元が3サンプルより短い場合、最大値は存在できず、警告が表示されます。
注記
この関数は、以下の考え方に基づいて動作します。
画像の最後の次元を最初にパスし、1つの方向のみでピクセルを比較することにより、局所的最大値の候補にフラグを立てます。ピクセルが最後の次元で接続されていない場合、すべてのピクセルが候補としてフラグ付けされます。
各候補について
フラッドフィルを実行して、同じグレイ値を持ち、プラトーの一部であるすべての接続ピクセルを見つけます。
プラトーの連結近傍を考慮します。境界サンプルにグレイレベルが高いものがない場合、プラトーを明確な局所的最大値としてマークします。
例
>>> from skimage.morphology import local_maxima >>> image = np.zeros((4, 7), dtype=int) >>> image[1:3, 1:3] = 1 >>> image[3, 0] = 1 >>> image[1:3, 4:6] = 2 >>> image[3, 6] = 3 >>> image array([[0, 0, 0, 0, 0, 0, 0], [0, 1, 1, 0, 2, 2, 0], [0, 1, 1, 0, 2, 2, 0], [1, 0, 0, 0, 0, 0, 3]])
すべての隣接ピクセル(最大接続)と比較して局所的最大値を見つける
>>> local_maxima(image) array([[False, False, False, False, False, False, False], [False, True, True, False, False, False, False], [False, True, True, False, False, False, False], [ True, False, False, False, False, False, True]]) >>> local_maxima(image, indices=True) (array([1, 1, 2, 2, 3, 3]), array([1, 2, 1, 2, 0, 6]))
対角ピクセル(接続1)と比較せずに局所的最大値を見つける
>>> local_maxima(image, connectivity=1) array([[False, False, False, False, False, False, False], [False, True, True, False, True, True, False], [False, True, True, False, True, True, False], [ True, False, False, False, False, False, True]])
画像のエッジに接する最大値を除外する
>>> local_maxima(image, connectivity=1, allow_borders=False) array([[False, False, False, False, False, False, False], [False, True, True, False, True, True, False], [False, True, True, False, True, True, False], [False, False, False, False, False, False, False]])
- skimage.morphology.local_minima(image, footprint=None, connectivity=None, indices=False, allow_borders=True)[source]#
n次元配列の局所的最小値を見つけます。
局所的最小値は、近傍のすべてのピクセルのグレイレベルよりも厳密に小さい、等しいグレイレベル(プラトー)を持つピクセルの連結集合として定義されます。
- パラメータ:
- **image**: ndarray
n次元配列。
- footprintndarray、オプション
各評価ピクセルの近傍を決定するために使用されるフットプリント(構造化要素)(
Trueは接続されたピクセルを示します)。これはブール値の配列でなければならず、imageと同じ次元数を持たなければなりません。footprintもconnectivityも指定されていない場合、すべての隣接ピクセルが近傍の一部とみなされます。- connectivityint、オプション
各評価ピクセルの近傍を決定するために使用される数値。中心からの二乗距離が
connectivity以下の隣接ピクセルは、近傍と見なされます。footprintが None でない場合は無視されます。- indicesブール値、オプション
Trueの場合、出力は各次元における局所的最小値のインデックスを表す1次元配列のタプルになります。Falseの場合、出力は
imageと同じ形状を持つブール値の配列になります。- allow_bordersブール値、オプション
trueの場合、画像の境界線に接するプラトーは有効な最小値となります。
- 戻り値:
- minimandarray または tuple[ndarray]
もし`indices`がfalseの場合、`image`と同じ形状のブール値配列が返され、`True`はローカルミニマの位置を示し(そうでない場合は`False`)、`indices`がtrueの場合、見つかったすべてのミニマの座標(インデックス)を含む1次元配列のタプルが返されます。
注記
この関数は、以下の考え方に基づいて動作します。
画像の最後の次元を最初にパスし、1方向のピクセルのみを比較することで、ローカルミニマの候補にフラグを立てます。ピクセルが最後の次元で接続されていない場合、すべてのピクセルが代わりに候補としてフラグ付けされます。
各候補について
フラッドフィルを実行して、同じグレイ値を持ち、プラトーの一部であるすべての接続ピクセルを見つけます。
プラトーの連結近傍を考えます。境界サンプルにグレースケール値が小さいものがない場合、プラトーを明確なローカルミニマとしてマークします。
例
>>> from skimage.morphology import local_minima >>> image = np.zeros((4, 7), dtype=int) >>> image[1:3, 1:3] = -1 >>> image[3, 0] = -1 >>> image[1:3, 4:6] = -2 >>> image[3, 6] = -3 >>> image array([[ 0, 0, 0, 0, 0, 0, 0], [ 0, -1, -1, 0, -2, -2, 0], [ 0, -1, -1, 0, -2, -2, 0], [-1, 0, 0, 0, 0, 0, -3]])
すべての隣接ピクセル(最大接続性)と比較してローカルミニマを見つけます
>>> local_minima(image) array([[False, False, False, False, False, False, False], [False, True, True, False, False, False, False], [False, True, True, False, False, False, False], [ True, False, False, False, False, False, True]]) >>> local_minima(image, indices=True) (array([1, 1, 2, 2, 3, 3]), array([1, 2, 1, 2, 0, 6]))
対角ピクセル(接続性1)と比較せずにローカルミニマを見つけます
>>> local_minima(image, connectivity=1) array([[False, False, False, False, False, False, False], [False, True, True, False, True, True, False], [False, True, True, False, True, True, False], [ True, False, False, False, False, False, True]])
画像のエッジに接するミニマを除外します
>>> local_minima(image, connectivity=1, allow_borders=False) array([[False, False, False, False, False, False, False], [False, True, True, False, True, True, False], [False, True, True, False, True, True, False], [False, False, False, False, False, False, False]])
- `skimage.morphology.max_tree(image, connectivity=1)`
画像から最大ツリーを構築します。
コンポーネントツリーは、画像に適用される連続的なしきい値処理操作から生じる連結成分の階層構造を表します。あるレベルの連結成分は、後者が最初のレベルに含まれている場合、より高いレベルの成分の親です。max-treeは、コンポーネントツリーの効率的な表現です。あるレベルの連結成分は、このレベルの1つの参照ピクセルで表され、そのレベルの他のすべてのピクセルとその上のレベルの参照ピクセルの親になります。max-treeは、多くの形態学的演算子、つまり連結演算子の基礎となります。
- パラメータ:
- **image**: ndarray
max-treeを計算する入力画像。この画像は任意のタイプにすることができます。
- **connectivity**: 符号なし整数、オプション
近傍接続性。整数は、隣接に到達するための直交ステップの最大数を表します。2Dでは、4近傍の場合は1、8近傍の場合は2です。デフォルト値は1です。
- 戻り値:
- **parent**: ndarray, int64
画像と同じ形状の配列。各ピクセルの値は、ravelled配列内の親のインデックスです。
- **tree_traverser**: 1D array, int64
順序付けられたピクセルインデックス(ravelled配列を参照)。ピクセルは、すべてのピクセルがその親の前に来るように順序付けられます(親のないルートを除く)。
参考文献
[1]Salembier, P., Oliveras, A., & Garrido, L. (1998). Antiextensive Connected Operators for Image and Sequence Processing. IEEE Transactions on Image Processing, 7(4), 555-570. DOI:10.1109/83.663500
[2]Berger, C., Geraud, T., Levillain, R., Widynski, N., Baillard, A., Bertin, E. (2007). Effective Component Tree Computation with Application to Pattern Recognition in Astronomical Imaging. In International Conference on Image Processing (ICIP) (pp. 41-44). DOI:10.1109/ICIP.2007.4379949
[3]Najman, L., & Couprie, M. (2006). Building the component tree in quasi-linear time. IEEE Transactions on Image Processing, 15(11), 3531-3539. DOI:10.1109/TIP.2006.877518
[4]Carlinet, E., & Geraud, T. (2014). A Comparative Review of Component Tree Computation Algorithms. IEEE Transactions on Image Processing, 23(9), 3885-3895. DOI:10.1109/TIP.2014.2336551
例
小さなサンプル画像([4]の図1)を作成し、max-treeを構築します。
>>> image = np.array([[15, 13, 16], [12, 12, 10], [16, 12, 14]]) >>> P, S = max_tree(image, connectivity=2)
- `skimage.morphology.max_tree_local_maxima(image, connectivity=1, parent=None, tree_traverser=None)`
画像のすべての局所的最大値を決定します。
ローカル maxima は、セットの直接近傍にあるすべてのピクセルのグレースケール値よりも厳密に大きい、等しいグレースケール値を持つピクセルの連結セットとして定義されます。この関数は、ローカル maxima にラベルを付けます。
技術的には、実装は画像のmax-tree表現に基づいています。max-tree表現がすでに計算されている場合、この関数は非常に効率的です。そうでない場合は、関数local_maximaを使用することをお勧めします。
- パラメータ:
- **image**: ndarray
最大値を計算する入力画像。
- **connectivity**: 符号なし整数、オプション
近傍接続性。整数は、隣接に到達するための直交ステップの最大数を表します。2Dでは、4近傍の場合は1、8近傍の場合は2です。デフォルト値は1です。
- **parent**: ndarray、int64、オプション
各ピクセルの値は、ravelled配列内の親のインデックスです。
- **tree_traverser**: 1D配列、int64、オプション
順序付けられたピクセルインデックス(ravelled配列を参照)。ピクセルは、すべてのピクセルがその親の前に来るように順序付けられます(親のないルートを除く)。
- 戻り値:
- **local_max**: ndarray, uint64
画像のラベル付けされたローカル maxima。
参考文献
[1]Vincent L., Proc. “Grayscale area openings and closings, their efficient implementation and applications”, EURASIP Workshop on Mathematical Morphology and its Applications to Signal Processing, Barcelona, Spain, pp.22-27, May 1993.
[2]Soille, P., “Morphological Image Analysis: Principles and Applications” (Chapter 6), 2nd edition (2003), ISBN 3540429883. DOI:10.1007/978-3-662-05088-0
[3]Salembier, P., Oliveras, A., & Garrido, L. (1998). Antiextensive Connected Operators for Image and Sequence Processing. IEEE Transactions on Image Processing, 7(4), 555-570. DOI:10.1109/83.663500
[4]Najman, L., & Couprie, M. (2006). Building the component tree in quasi-linear time. IEEE Transactions on Image Processing, 15(11), 3531-3539. DOI:10.1109/TIP.2006.877518
[5]Carlinet, E., & Geraud, T. (2014). A Comparative Review of Component Tree Computation Algorithms. IEEE Transactions on Image Processing, 23(9), 3885-3895. DOI:10.1109/TIP.2014.2336551
例
画像を作成します(中央に最大値があり、4つの追加の定数最大値を持つ2次関数)。
>>> w = 10 >>> x, y = np.mgrid[0:w,0:w] >>> f = 20 - 0.2*((x - w/2)**2 + (y-w/2)**2) >>> f[2:4,2:4] = 40; f[2:4,7:9] = 60; f[7:9,2:4] = 80; f[7:9,7:9] = 100 >>> f = f.astype(int)
すべてのローカル maxima を計算できます
>>> maxima = max_tree_local_maxima(f)
結果の画像には、ラベル付けされたローカル maxima が含まれています。
- `skimage.morphology.medial_axis(image, mask=None, return_distance=False, *, rng=None)`
バイナリ画像の中軸変換を計算します。
- パラメータ:
- **image**: binary ndarray, shape (M, N)
スケルトン化する形状の画像。この入力がまだバイナリ画像でない場合は、バイナリ画像に変換されます。この場合、ゼロ値は背景(False)と見なされ、ゼロ以外の値は前景(True)と見なされます。
- **mask**: binary ndarray, shape (M, N), optional
マスクが指定されている場合、`mask`の値がtrueである`image`の要素のみがmedial axisの計算に使用されます。
- **return_distance**: bool, optional
trueの場合、距離変換とスケルトンが返されます。
- **rng**: {`numpy.random.Generator`, int}, optional
疑似乱数ジェネレータ。デフォルトでは、PCG64ジェネレータが使用されます(`numpy.random.default_rng()`を参照)。`rng`がintの場合、ジェネレータをシードするために使用されます。
PRNGは、タイブレークのためにピクセルが処理される順序を決定します。
バージョン0.19で追加されました。
- 戻り値:
- **out**: ndarray of bools
画像のmedial axis変換
- **dist**: ndarray of ints, optional
画像の距離変換(`return_distance`がTrueの場合のみ返されます)
参照
- `skeletonize`, `thin`
注記
このアルゴリズムは、画像のmedial axis変換を、その距離変換のリッジとして計算します。
- アルゴリズムのさまざまな手順は次のとおりです
ルックアップテーブルが使用され、3x3のバイナリ正方形の各構成に0または1が割り当てられます。これは、中央のピクセルを削除するか保持するかを示します。中心のピクセルが複数の隣接ピクセルを持ち、それを削除しても連結成分の数が変わらない場合、そのピクセルを削除します。
背景までの距離変換と、ピクセルのコーナーネスが計算されます。
前景(値1)のポイントは、距離変換、次にコーナーネスによって順序付けられます。
画像をスケルトンに縮小するために、cython関数が呼び出されます。前のステップで決定された順序でピクセルを処理し、ルックアップテーブルに従ってピクセルを削除または維持します。順序付けにより、すべてのピクセルを1パスだけで処理できます。
例
>>> square = np.zeros((7, 7), dtype=bool) >>> square[1:-1, 2:-2] = 1 >>> square.view(np.uint8) array([[0, 0, 0, 0, 0, 0, 0], [0, 0, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 0, 0], [0, 0, 0, 0, 0, 0, 0]], dtype=uint8) >>> medial_axis(square).view(np.uint8) array([[0, 0, 0, 0, 0, 0, 0], [0, 0, 1, 0, 1, 0, 0], [0, 0, 0, 1, 0, 0, 0], [0, 0, 0, 1, 0, 0, 0], [0, 0, 0, 1, 0, 0, 0], [0, 0, 1, 0, 1, 0, 0], [0, 0, 0, 0, 0, 0, 0]], dtype=uint8)
- `skimage.morphology.mirror_footprint(footprint)`
フットプリントの各次元を反転します。
- パラメータ:
- footprintndarray または タプル
入力フットプリントまたはフットプリントのシーケンス
- 戻り値:
- **inverted**: ndarray or tuple
フットプリント。各次元でミラーリングされます。
例
>>> footprint = np.array([[0, 0, 0], ... [0, 1, 1], ... [0, 1, 1]], np.uint8) >>> mirror_footprint(footprint) array([[1, 1, 0], [1, 1, 0], [0, 0, 0]], dtype=uint8)
- `skimage.morphology.octagon(m, n, dtype=<class 'numpy.uint8'>, *, decomposition=None)`
八角形のフットプリントを生成します。
指定されたサイズ(m)の水平方向および垂直方向の辺と、指定されたサイズ(n)の斜めの辺の高さまたは幅について、八角形が生成されます。斜めの辺は水平軸に対して45度または135度であるため、幅と高さは等しくなります。フットプリントの単一軸に沿った全体のサイズは `m + 2 * n` になります。
- パラメータ:
- **m**: int
水平方向と垂直方向の辺のサイズ。
- **n**: int
斜めの辺の高さまたは幅。
- 戻り値:
- footprintndarray または タプル
近傍の要素が1で、それ以外の場合は0であるフットプリント。`decomposition`がNoneの場合、これは単なるnumpy.ndarrayです。それ以外の場合、これは適用する一意の構造化要素の数に等しい長さのタプルになります(詳細については注記を参照)。
- その他の引数:
- dtypeデータ型、オプション
フットプリントのデータ型。
- decomposition{None, 'sequence'}、オプション
Noneの場合、単一の配列が返されます。「sequence」の場合、より小さなフットプリントのタプルが返されます。この一連の小さなフットプリントを適用すると、単一の大きなフットプリントと同じ結果が得られますが、計算パフォーマンスが向上します。詳細については、注記を参照してください。
注記
`decomposition`がNoneでない場合、`footprint`タプルの各要素は、フットプリント配列とそれが適用される反復回数を指定する`(ndarray、num_iter)`形式の2タプルです。
バイナリまたはグレースケールのモルフォロジーのいずれの場合でも、`decomposition='sequence'`を使用すると、パフォーマンス上の利点があり、フットプリントサイズが大きくなるほど利点の大きさが増すことが観察されました。
- `skimage.morphology.octahedron(radius, dtype=<class 'numpy.uint8'>, *, decomposition=None)`
八面体型のフットプリントを生成します。
これはダイヤモンドの3次元版です。ピクセルとその近傍の中心との間の都市ブロック/マンハッタン距離が半径以下である場合、ピクセルは近傍の一部です(つまり、1とラベル付けされます)。
- パラメータ:
- radiusint
八面体形状のフットプリントの半径。
- 戻り値:
- footprintndarray または タプル
近傍の要素が1で、それ以外の場合は0であるフットプリント。`decomposition`がNoneの場合、これは単なるnumpy.ndarrayです。それ以外の場合、これは適用する一意の構造化要素の数に等しい長さのタプルになります(詳細については注記を参照)。
- その他の引数:
- dtypeデータ型、オプション
フットプリントのデータ型。
- decomposition{None, 'sequence'}、オプション
Noneの場合、単一の配列が返されます。「sequence」の場合、より小さなフットプリントのタプルが返されます。この一連の小さなフットプリントを適用すると、単一の大きなフットプリントと同じ結果が得られますが、計算パフォーマンスが向上します。詳細については、注記を参照してください。
注記
`decomposition`がNoneでない場合、`footprint`タプルの各要素は、フットプリント配列とそれが適用される反復回数を指定する`(ndarray、num_iter)`形式の2タプルです。
バイナリまたはグレースケールのモルフォロジーのいずれの場合でも、`decomposition='sequence'`を使用すると、パフォーマンス上の利点があり、フットプリントサイズが大きくなるほど利点の大きさが増すことが観察されました。
- skimage.morphology.opening(image, footprint=None, out=None, *, mode='reflect', cval=0.0)[source]#
画像のグレースケールモルフォロジーオープニングを返します。
画像のモルフォロジーオープニングは、エロージョンに続いてダイレーションを行うことで定義されます。オープニングは、小さな明るいスポット(つまり「塩」)を除去し、小さな暗い亀裂を接続することができます。これは、(明るい)特徴間の(暗い)ギャップを「開く」傾向があります。
- パラメータ:
- **image**: ndarray
画像配列。
- footprintndarray または タプル、オプション
1と0の2次元配列として表される近傍。 Noneの場合、十字型のフットプリント(connectivity = 1)を使用します。 フットプリントは、以下の注記で説明されているように、より小さなフットプリントのシーケンスとして提供することもできます。
- outndarray、オプション
モルフォロジーの結果を格納する配列。 Noneが渡された場合は、新しい配列が割り当てられます。
- mode文字列、オプション
modeパラメータは、配列の境界をどのように処理するかを決定します。有効なモードは、「reflect」、「constant」、「nearest」、「mirror」、「wrap」、「max」、「min」、または「ignore」です。「ignore」の場合、画像領域外のピクセルは、収縮では画像のデータ型の最大値、膨張では最小値と見なされ、結果に影響を与えません。デフォルトは「reflect」です。- cvalスカラー、オプション
modeが「constant」の場合、入力のエッジを越えた部分を埋める値。デフォルトは 0.0 です。バージョン 0.23 で追加:
modeとcvalは 0.23 で追加されました。
- 戻り値:
- opening`image`と同じ形状とタイプの配列
モルフォロジー opening の結果。
注記
フットプリントは、2タプルのシーケンスとして提供することもできます。各2タプルの最初の要素はフットプリントndarrayで、2番目の要素は反復する回数を表す整数です。 たとえば、
footprint=[(np.ones((9, 1)), 1), (np.ones((1, 9)), 1)]は、9x1フットプリントに続いて1x9フットプリントを適用します。その結果、footprint=np.ones((9, 9))と同じ効果が得られますが、計算コストは低くなります。skimage.morphology.disk()などの組み込みフットプリントのほとんどは、このタイプのフットプリントシーケンスを自動的に生成するオプションを提供します。例
>>> # Open up gap between two bright regions (but also shrink regions) >>> import numpy as np >>> from skimage.morphology import footprint_rectangle >>> bad_connection = np.array([[1, 0, 0, 0, 1], ... [1, 1, 0, 1, 1], ... [1, 1, 1, 1, 1], ... [1, 1, 0, 1, 1], ... [1, 0, 0, 0, 1]], dtype=np.uint8) >>> opening(bad_connection, footprint_rectangle((3, 3))) array([[0, 0, 0, 0, 0], [1, 1, 0, 1, 1], [1, 1, 0, 1, 1], [1, 1, 0, 1, 1], [0, 0, 0, 0, 0]], dtype=uint8)
- skimage.morphology.pad_footprint(footprint, *, pad_end=True)[source]#
フットプリントを各次元で奇数サイズにパディングします。
- パラメータ:
- footprintndarray または タプル
入力フットプリントまたはフットプリントのシーケンス
- pad_endbool、オプション
Trueの場合、各次元の末尾(右側)にパディングを追加し、そうでない場合は先頭(左側)にパディングを追加します。
- 戻り値:
- paddedndarrayまたはタプル
各次元で奇数サイズにパディングされたフットプリント。
例
>>> footprint = np.array([[0, 0], ... [1, 1], ... [1, 1]], np.uint8) >>> pad_footprint(footprint) array([[0, 0, 0], [1, 1, 0], [1, 1, 0]], dtype=uint8)
- skimage.morphology.reconstruction(seed, mask, method='dilation', footprint=None, offset=None)[source]#
画像のモルフォロジー再構成を実行します。
ダイレーションによるモルフォロジー再構成は、基本的なモルフォロジーダイレーションに似ています。高輝度値は、近くの低輝度値を置き換えます。ただし、基本的なダイレーション演算子は、フットプリントを使用して、入力画像の値がどれだけ広がるかを決定します。対照的に、再構成では2つの画像を使用します。「シード」画像(拡散する値を指定)と「マスク」画像(各ピクセルで許容される最大値を与える)です。マスク画像は、フットプリントと同様に、高輝度値の拡散を制限します。エロージョンによる再構成は、単にその逆です。低輝度値はシード画像から拡散し、許容される最小値を表すマスク画像によって制限されます。
あるいは、再構成を画像の連結領域を分離する方法と考えることもできます。ダイレーションの場合、再構成はシード画像の局所的な最大値によってマークされた領域を接続します。これらのシード以下の隣接ピクセルは、シードされた領域に接続されます。シード画像よりも大きい値を持つ局所的な最大値は、シード値に切り捨てられます。
- パラメータ:
- **seed**ndarray
シード画像(別名マーカー画像)。ダイレーションまたはエロージョンされる値を指定します。
- maskndarray
各ピクセルで許容される最大値(ダイレーション)/最小値(エロージョン)。
- **method**{‘dilation’|’erosion’}、オプション
ダイレーションまたはエロージョンによって再構成を実行します。ダイレーション(またはエロージョン)では、シード画像はマスク画像によって制限されるまでダイレーション(またはエロージョン)されます。ダイレーションの場合、各シード値は対応するマスク値以下である必要があります。エロージョンの場合は、逆が真です。デフォルトは「dilation」です。
- footprintndarray、オプション
1と0のn次元配列として表される近傍。デフォルトは、半径が1に等しいn次元正方形です(つまり、2D画像の場合は3x3正方形、3D画像の場合は3x3x3立方体など)。
- **offset**ndarray、オプション
フットプリントの中心の座標。デフォルトはフットプリントの幾何学的中心に配置されます。その場合、フットプリントの次元は奇数である必要があります。
- 戻り値:
- **reconstructed**ndarray
モルフォロジー再構成の結果。
注記
アルゴリズムは[1]から引用しています。グレースケール再構成のアプリケーションについては、[2]および[3]で説明しています。
参考文献
[1]Robinson、「Efficient morphological reconstruction: a downhill filter」、Pattern Recognition Letters 25 (2004) 1759-1767.
[2]Vincent, L.、「Morphological Grayscale Reconstruction in Image Analysis: Applications and Efficient Algorithms」、IEEE Transactions on Image Processing (1993)
[3]Soille, P.、「Morphological Image Analysis: Principles and Applications」、Chapter 6、第2版(2003)、ISBN 3540429883.
例
>>> import numpy as np >>> from skimage.morphology import reconstruction
まず、中央と端にピークを持つ正弦波マスク画像を作成します。
>>> x = np.linspace(0, 4 * np.pi) >>> y_mask = np.cos(x)
次に、最小マスク値(ダイレーションによる再構成の場合、最小輝度値は拡散しません)に初期化されたシード画像を作成し、左右のピークに「シード」を追加しますが、ピーク値の1分の1(1)にします。
>>> y_seed = y_mask.min() * np.ones_like(x) >>> y_seed[0] = 0.5 >>> y_seed[-1] = 0 >>> y_rec = reconstruction(y_seed, y_mask)
再構成された画像(またはこの場合は曲線)は、ピークが0.5と0に切り捨てられていることを除いて、マスク画像とまったく同じです。中央のピークは完全に消えます。このピーク領域にシード値がなかったため、その再構成値は周囲の値(-1)に切り捨てられます。
より実用的な例として、再構成によって作成された背景画像を減算することにより、画像の明るい特徴を抽出してみます。
>>> y, x = np.mgrid[:20:0.5, :20:0.5] >>> bumps = np.sin(x) + np.sin(y)
背景画像を作成するには、マスク画像を元の画像に設定し、シード画像を輝度オフセット
hを持つ元の画像に設定します。>>> h = 0.3 >>> seed = bumps - h >>> background = reconstruction(seed, bumps)
結果の再構成画像は、元の画像とまったく同じように見えますが、バンプのピークは切り取られています。この再構成画像を元の画像から減算すると、バンプのピークのみが残ります。
>>> hdome = bumps - background
この操作は、画像のhドームと呼ばれ、減算された画像に高さ
hの特徴を残します。
- skimage.morphology.remove_objects_by_distance(label_image, min_distance, *, priority=None, p_norm=2, spacing=None, out=None)[source]#
残りのオブジェクトが最小距離離れるまで、指定された順序でオブジェクトを削除します。
残りのオブジェクトが互いに特定の距離以上離れるまで、画像からラベル付けされたオブジェクトを削除します。デフォルトでは、小さいオブジェクトが最初に削除されます。
- パラメータ:
- **label_image**整数のndarray
label()によって返されるような、オブジェクトラベルを含むn次元配列。値ゼロは背景と見なされ、他のすべてのオブジェクトIDは正の整数である必要があります。- **min_distance**intまたはfloat
他のオブジェクトまでの距離がこの正の値以下のオブジェクトを削除します。
priorityが低いオブジェクトが最初に削除されます。- **priority**ndarray、オプション
オブジェクトが削除される優先順位を定義します。長さ
np.amax(label_image) + 1の1次元配列を想定しており、それぞれのインデックスに各オブジェクトのラベルの優先順位が含まれています。値が小さいオブジェクトは、残りのすべてのオブジェクトが距離要件を満たすまで、最初に削除されます。指定しない場合、サンプル数が多いオブジェクトと、次にラベル値が高いオブジェクトが優先されます。- **p_norm**intまたはfloat、オプション
オブジェクト間の距離を計算するために使用される、次数pのミンコフスキー距離。デフォルトの
2はユークリッド距離、1は「マンハッタン」距離、np.infはチェビシェフ距離に対応します。- **spacing**floatのシーケンス、オプション
label_imageの各軸に沿ったピクセル間隔。指定しない場合、単位(1)のグリッド間隔が暗示されます。- outndarray、オプション
出力が配置される、
imageと同じ形状とdtypeの配列。デフォルトでは、新しい配列が作成されます。
- 戻り値:
- **out**ndarray
``label_image`` と同じ形状の配列で、 ``min_distance`` 条件に違反するオブジェクトが削除されています。
参照
skimage.morphology.remove_small_objects指定されたサイズより小さいオブジェクトを削除します。
注記
このアルゴリズムの基本的な手順は以下のとおりです。
指定されたすべてのオブジェクトのインデックスを見つけ、オブジェクトの境界を指しているかどうかで分離します。
ラベル値でインデックスをソートし、同じオブジェクトを指すインデックスが隣り合うようにします。この最適化により、隣接するインデックスにステップするだけで、オブジェクトのすべての部分を見つけることができます。
境界インデックスを ``priority`` でソートします。前のソート手順からの順序を保持するために、安定ソートを使用します。 ``priority`` が指定されていない場合は、フォールバックとして
numpy.bincount()を使用します。境界インデックスから
scipy.spatial.cKDTreeを構築します。優先順位でソートされた境界インデックスを反復処理し、近すぎるオブジェクトをkdツリーにクエリします。近すぎるオブジェクトを削除し、後で他のオブジェクトを評価する際には考慮しません。
このアルゴリズムのパフォーマンスは、オブジェクトの境界に属する ``label_image`` のサンプル数に依存します。
例
>>> import skimage as ski >>> ski.morphology.remove_objects_by_distance(np.array([2, 0, 1, 1]), 2) array([0, 0, 1, 1]) >>> ski.morphology.remove_objects_by_distance( ... np.array([2, 0, 1, 1]), 2, priority=np.array([0, 1, 9]) ... ) array([2, 0, 0, 0]) >>> label_image = np.array( ... [[8, 0, 0, 0, 0, 0, 0, 0, 0, 9, 9], ... [8, 8, 8, 0, 0, 0, 0, 0, 0, 9, 9], ... [0, 0, 0, 0, 0, 0, 0, 0, 9, 0, 0], ... [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], ... [0, 0, 3, 0, 0, 0, 1, 0, 0, 0, 0], ... [2, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0, 0, 0, 7, 7]] ... ) >>> ski.morphology.remove_objects_by_distance( ... label_image, min_distance=3 ... ) array([[8, 0, 0, 0, 0, 0, 0, 0, 0, 9, 9], [8, 8, 8, 0, 0, 0, 0, 0, 0, 9, 9], [0, 0, 0, 0, 0, 0, 0, 0, 9, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 7, 7]])
- skimage.morphology.remove_small_holes(ar, area_threshold=64, connectivity=1, *, out=None)[source]#
指定されたサイズより小さい連続した穴を削除します。
- パラメータ:
- **ar**ndarray (任意の形状、int または bool 型)
対象の連結成分を含む配列。
- **area_threshold**int, optional (デフォルト: 64)
塗りつぶされる連続した穴の最大面積 (ピクセル単位)。 ``min_size`` を置き換えます。
- **connectivity**int, {1, 2, …, ar.ndim}, optional (デフォルト: 1)
ピクセルの近傍を定義する接続性。
- **out**ndarray
``ar`` と同じ形状と bool 型の配列で、出力結果が格納されます。デフォルトでは、新しい配列が作成されます。
- 戻り値:
- **out**ndarray, 入力 ``ar`` と同じ形状と型
連結成分内の小さな穴が除去された入力配列。
- 発生する例外:
- TypeError
入力配列の型が無効な場合 (float や string など)。
- ValueError
入力配列に負の値が含まれている場合。
注記
配列の型が int の場合、既にラベル付けされたオブジェクトが含まれていると想定されます。ラベルは出力画像には保持されません (この関数は常に bool 画像を出力します)。この関数を使用した後にラベル付けを行うことをお勧めします。
例
>>> from skimage import morphology >>> a = np.array([[1, 1, 1, 1, 1, 0], ... [1, 1, 1, 0, 1, 0], ... [1, 0, 0, 1, 1, 0], ... [1, 1, 1, 1, 1, 0]], bool) >>> b = morphology.remove_small_holes(a, 2) >>> b array([[ True, True, True, True, True, False], [ True, True, True, True, True, False], [ True, False, False, True, True, False], [ True, True, True, True, True, False]]) >>> c = morphology.remove_small_holes(a, 2, connectivity=2) >>> c array([[ True, True, True, True, True, False], [ True, True, True, False, True, False], [ True, False, False, True, True, False], [ True, True, True, True, True, False]]) >>> d = morphology.remove_small_holes(a, 2, out=a) >>> d is a True
- skimage.morphology.remove_small_objects(ar, min_size=64, connectivity=1, *, out=None)[source]#
指定されたサイズより小さいオブジェクトを削除します。
ar はラベル付けされたオブジェクトを含む配列であると想定し、 ``min_size`` より小さいオブジェクトを削除します。 ``ar`` が bool の場合、画像は最初にラベル付けされます。これにより、bool 型と 0 と 1 の配列で動作が異なる可能性があります。
- パラメータ:
- **ar**ndarray (任意の形状、int または bool 型)
対象のオブジェクトを含む配列。配列の型が int の場合、int は非負でなければなりません。
- **min_size**int, optional (デフォルト: 64)
許容される最小オブジェクトサイズ。
- **connectivity**int, {1, 2, …, ar.ndim}, optional (デフォルト: 1)
ピクセルの近傍を定義する接続性。 ``ar`` が bool の場合、ラベル付け中に使用されます。
- **out**ndarray
``ar`` と同じ形状の配列で、出力結果が格納されます。デフォルトでは、新しい配列が作成されます。
- 戻り値:
- **out**ndarray, 入力 ``ar`` と同じ形状と型
小さな連結成分が除去された入力配列。
- 発生する例外:
- TypeError
入力配列の型が無効な場合 (float や string など)。
- ValueError
入力配列に負の値が含まれている場合。
例
>>> from skimage import morphology >>> a = np.array([[0, 0, 0, 1, 0], ... [1, 1, 1, 0, 0], ... [1, 1, 1, 0, 1]], bool) >>> b = morphology.remove_small_objects(a, 6) >>> b array([[False, False, False, False, False], [ True, True, True, False, False], [ True, True, True, False, False]]) >>> c = morphology.remove_small_objects(a, 7, connectivity=2) >>> c array([[False, False, False, True, False], [ True, True, True, False, False], [ True, True, True, False, False]]) >>> d = morphology.remove_small_objects(a, 6, out=a) >>> d is a True
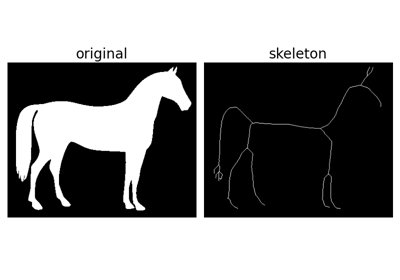
- skimage.morphology.skeletonize(image, *, method=None)[source]#
間引きによって入力画像のスケルトンを計算します。
- パラメータ:
- **image**(M, N[, P]) ndarray of bool or int
スケルトン化されるオブジェクトを含む画像。画像内の各連結成分は、1ピクセル幅のスケルトンに縮小されます。画像は間引き処理前に二値化されます。したがって、強度が異なる隣接するオブジェクトは1つと見なされます。ゼロまたは ``False`` 値は背景を表し、ゼロ以外または ``True`` 値は前景を表します。
- **method**{‘zhang’, ‘lee’}, optional
使用するアルゴリズム。Zhangのアルゴリズム[Zha84]は2D画像にのみ有効で、2Dのデフォルトです。Leeのアルゴリズム[Lee94]は2Dまたは3D画像に有効で、3Dのデフォルトです。
- 戻り値:
- **skeleton**(M, N[, P]) ndarray of bool
間引きされた画像。
参照
参考文献
[Lee94]T.-C. Lee, R.L. Kashyap and C.-N. Chu, Building skeleton models via 3-D medial surface/axis thinning algorithms. Computer Vision, Graphics, and Image Processing, 56(6):462-478, 1994.
[Zha84]A fast parallel algorithm for thinning digital patterns, T. Y. Zhang and C. Y. Suen, Communications of the ACM, March 1984, Volume 27, Number 3.
例
>>> X, Y = np.ogrid[0:9, 0:9] >>> ellipse = (1./3 * (X - 4)**2 + (Y - 4)**2 < 3**2).astype(bool) >>> ellipse.view(np.uint8) array([[0, 0, 0, 1, 1, 1, 0, 0, 0], [0, 0, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 0, 0], [0, 0, 0, 1, 1, 1, 0, 0, 0]], dtype=uint8) >>> skel = skeletonize(ellipse) >>> skel.view(np.uint8) array([[0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 1, 0, 0, 0, 0], [0, 0, 0, 0, 1, 0, 0, 0, 0], [0, 0, 0, 0, 1, 0, 0, 0, 0], [0, 0, 0, 0, 1, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0]], dtype=uint8)
- skimage.morphology.star(a, dtype=<class 'numpy.uint8'>)[source]#
星型のフットプリントを生成します。
星型は8つの頂点があり、サイズ ``2*a + 1`` の正方形とその45度回転バージョンのオーバーラップです。傾斜した辺は水平軸に対して45度または135度です。
- パラメータ:
- **a**int
星型構造要素のサイズを決定するパラメータ。返される正方配列の辺は ``2*a + 1 + 2*floor(a / 2)`` です。
- 戻り値:
- footprintndarray
近傍の要素が1、それ以外の要素が0であるフットプリント。
- その他の引数:
- dtypeデータ型、オプション
フットプリントのデータ型。
- skimage.morphology.thin(image, max_num_iter=None)[source]#
バイナリ画像のモルフォロジー細線化を実行します。
- パラメータ:
- **image**二値 (M, N) ndarray
間引きする画像。この入力がまだ二値画像でない場合、二値画像に変換されます。この場合、ゼロ値は背景 (False) と見なされ、ゼロ以外の値は前景 (True) と見なされます。
- **max_num_iter**int, 反復回数, optional
このパラメータの値に関係なく、反復処理によって変更が発生しない場合は、間引きされた画像がすぐに返されます。このパラメータを指定すると、実行される反復回数の最大値が設定されます。
- 戻り値:
- **out**bool の ndarray
間引きされた画像。
注記
このアルゴリズム[1]は、画像を複数回パスすることで機能し、8連結成分と2 x 2の正方形[2]を保持しながら連結領域を間引くように設計された一連の基準に一致するピクセルを削除します。2つのサブイテレーションのそれぞれで、アルゴリズムは中間スケルトン画像を近傍マスクと相関させ、次に各近傍をルックアップテーブルで調べ、そのサブイテレーションで中央ピクセルを削除するかどうかを示します。
参考文献
[1]Z. Guo and R. W. Hall, “Parallel thinning with two-subiteration algorithms,” Comm. ACM, vol. 32, no. 3, pp. 359-373, 1989. DOI:10.1145/62065.62074
[2]Lam, L., Seong-Whan Lee, and Ching Y. Suen, “Thinning Methodologies-A Comprehensive Survey,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol 14, No. 9, p. 879, 1992. DOI:10.1109/34.161346
例
>>> square = np.zeros((7, 7), dtype=bool) >>> square[1:-1, 2:-2] = 1 >>> square[0, 1] = 1 >>> square.view(np.uint8) array([[0, 1, 0, 0, 0, 0, 0], [0, 0, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 0, 0], [0, 0, 0, 0, 0, 0, 0]], dtype=uint8) >>> skel = thin(square) >>> skel.view(np.uint8) array([[0, 1, 0, 0, 0, 0, 0], [0, 0, 1, 0, 0, 0, 0], [0, 0, 0, 1, 0, 0, 0], [0, 0, 0, 1, 0, 0, 0], [0, 0, 0, 1, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0]], dtype=uint8)
- skimage.morphology.white_tophat(image, footprint=None, out=None, *, mode='reflect', cval=0.0)[source]#
画像のホワイトトップハットを返します。
画像のホワイトトップハットは、画像からそのモルフォロジーオープニングを差し引いたものとして定義されます。この操作は、フットプリントよりも小さい画像の輝点(明るいスポット)を返します。
- パラメータ:
- **image**: ndarray
画像配列。
- footprintndarray または タプル、オプション
1と0の2次元配列として表される近傍。 Noneの場合、十字型のフットプリント(connectivity = 1)を使用します。 フットプリントは、以下の注記で説明されているように、より小さなフットプリントのシーケンスとして提供することもできます。
- outndarray、オプション
モルフォロジーの結果を格納する配列。 Noneが渡された場合は、新しい配列が割り当てられます。
- mode文字列、オプション
modeパラメータは、配列の境界をどのように処理するかを決定します。有効なモードは、'reflect'、'constant'、'nearest'、'mirror'、'wrap'、'max'、'min'、または 'ignore' です。skimage.morphology.opening()を参照してください。デフォルトは 'reflect' です。- cvalスカラー、オプション
modeが「constant」の場合、入力のエッジを越えた部分を埋める値。デフォルトは 0.0 です。バージョン 0.23 で追加:
modeとcvalは 0.23 で追加されました。
- 戻り値:
- out
imageと同じ形状とタイプの配列 モルフォロジーホワイトトップハットの結果です。
- out
参照
注記
フットプリントは、2タプルのシーケンスとして提供することもできます。各2タプルの最初の要素はフットプリントndarrayで、2番目の要素は反復する回数を表す整数です。 たとえば、
footprint=[(np.ones((9, 1)), 1), (np.ones((1, 9)), 1)]は、9x1フットプリントに続いて1x9フットプリントを適用します。その結果、footprint=np.ones((9, 9))と同じ効果が得られますが、計算コストは低くなります。skimage.morphology.disk()などの組み込みフットプリントのほとんどは、このタイプのフットプリントシーケンスを自動的に生成するオプションを提供します。参考文献
例
>>> # Subtract gray background from bright peak >>> import numpy as np >>> from skimage.morphology import footprint_rectangle >>> bright_on_gray = np.array([[2, 3, 3, 3, 2], ... [3, 4, 5, 4, 3], ... [3, 5, 9, 5, 3], ... [3, 4, 5, 4, 3], ... [2, 3, 3, 3, 2]], dtype=np.uint8) >>> white_tophat(bright_on_gray, footprint_rectangle((3, 3))) array([[0, 0, 0, 0, 0], [0, 0, 1, 0, 0], [0, 1, 5, 1, 0], [0, 0, 1, 0, 0], [0, 0, 0, 0, 0]], dtype=uint8)