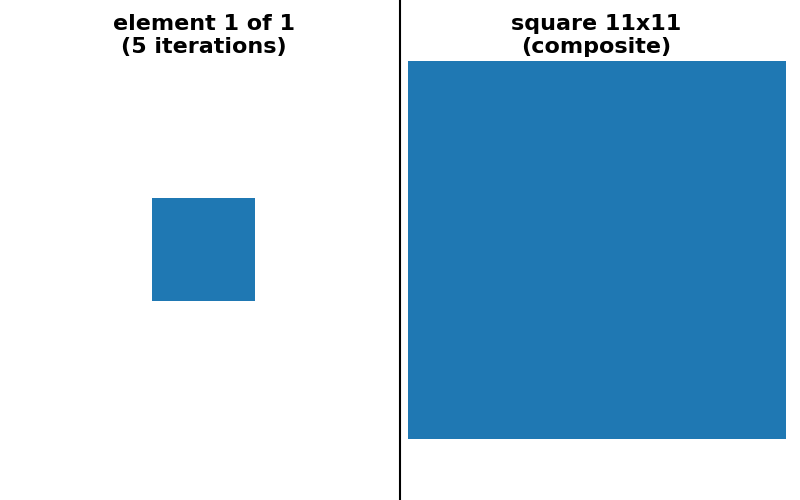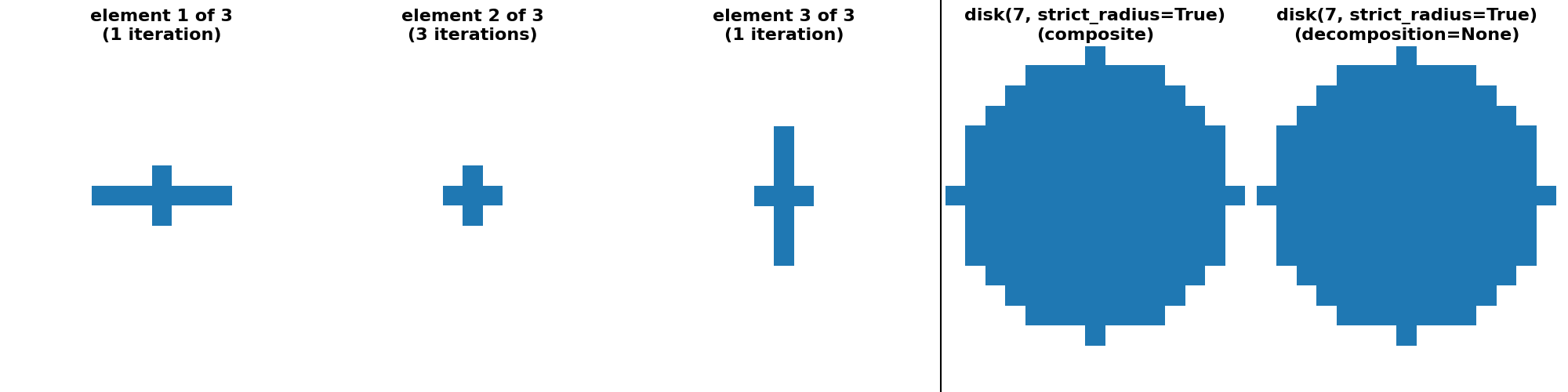注記
完全なサンプルコードをダウンロードするには、最後まで進んでください。 または、Binder を使用してブラウザでこの例を実行します。
フラットなフットプリント(構造要素)の分解#
多くのフットプリント(構造要素)は、同等のより小さな構造要素の系列に分解できます。「フラット」という用語は、0または1の値のみを含むフットプリントを指します(つまり、skimage.morphology.footprints内のすべてのメソッド)。バイナリ膨張演算は、多くの場合、より小さなフットプリントの同等の系列への分解を可能にする結合的および分配的特性を持っています。これは、パフォーマンス上の利点を得るために最も頻繁に行われます。
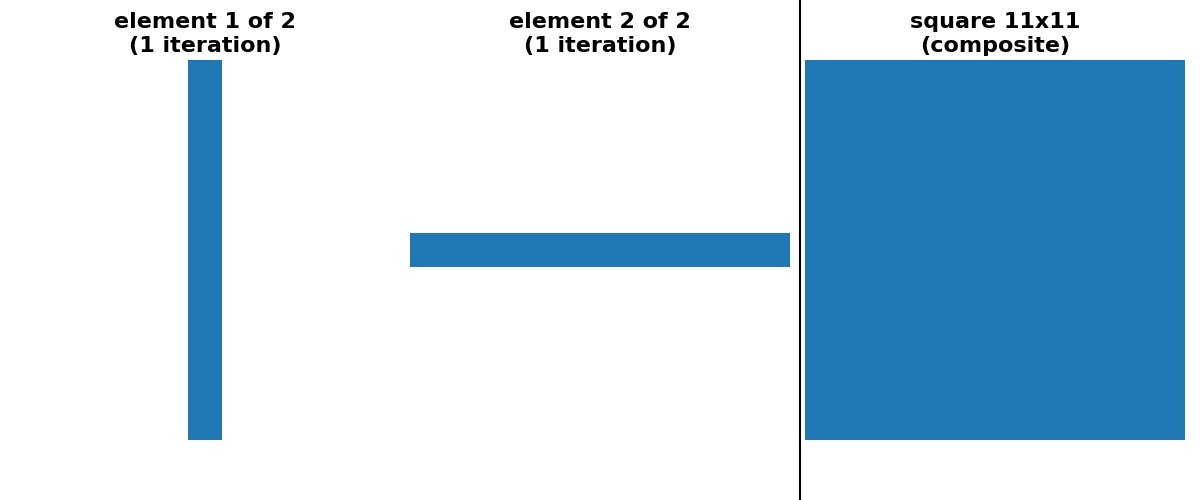
具体的な例として、(15, 15)の形状を持つ正方形のフットプリントによる膨張は、(15, 1)の形状を持つ長方形による膨張、続いて(1, 15)の形状を持つ長方形による別の膨張と同等です。(3, 3)の形状を持つ正方形のフットプリントによる7回の連続した膨張と同等でもあります。
多くの可能な分解があり、どれが最適に機能するかはアーキテクチャに依存する可能性があります。
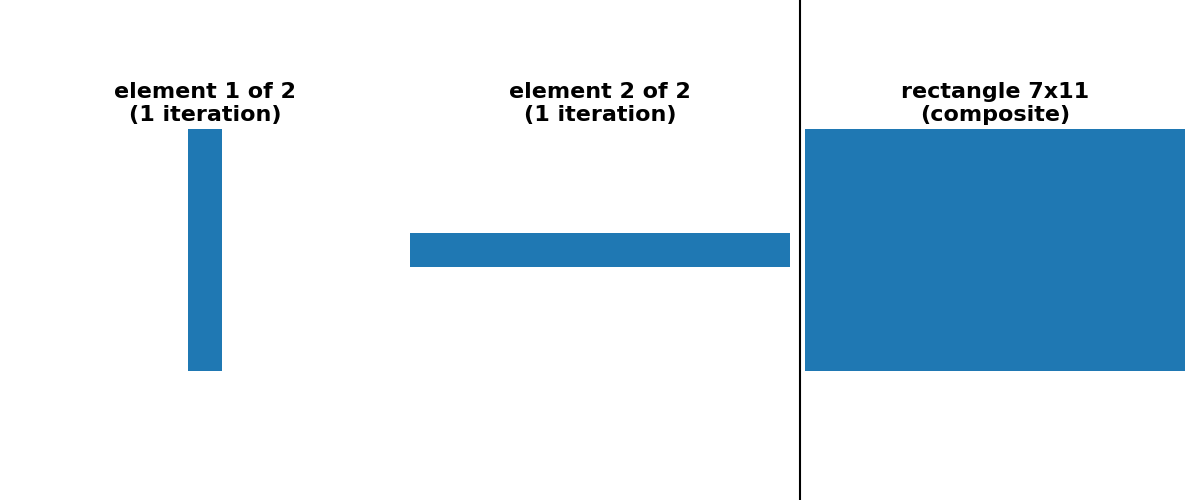
scikit-imageは現在、2種類の自動分解を提供しています。square、rectangle、cubeフットプリントの場合、「分離可能な」分解(1つの軸に沿ってのみサイズ>1)のオプションがあります。
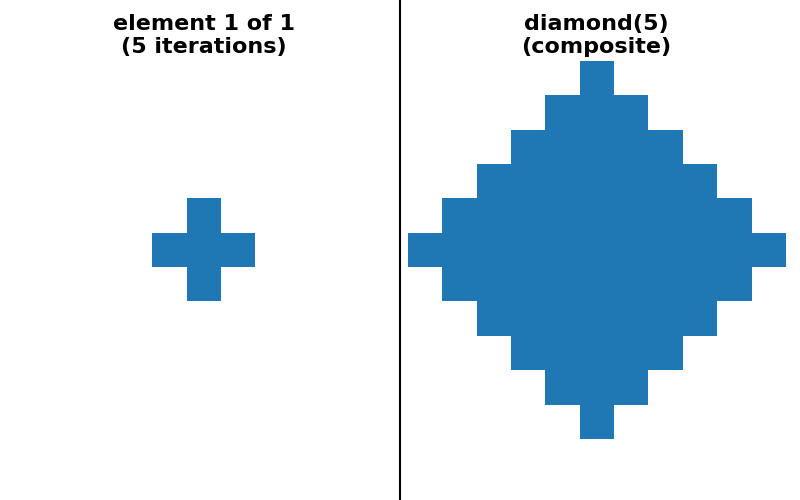
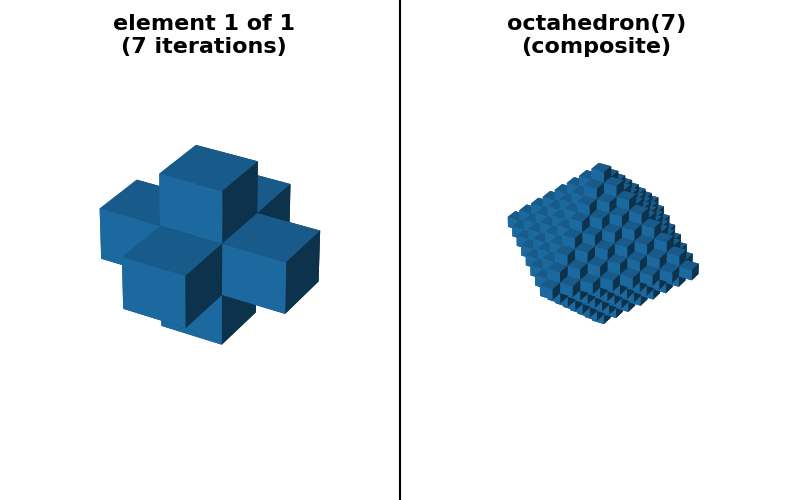
他のいくつかの対称凸形状、例えばdiamond、octahedron、octagonなどでは、1D演算への分離可能な分解はありません。しかし、(3,) * ndimの形状を持つ小さなフットプリントの系列に基づいた「シーケンス」分解を提供することは可能です。
実装の簡素化のために、以下に示すすべての分解では、フットプリントの中央に原点を持つ奇数サイズのフットプリントのみを使用しています。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import colors
from mpl_toolkits.mplot3d import Axes3D
from skimage.morphology import (
ball,
diamond,
disk,
ellipse,
octagon,
octahedron,
footprint_rectangle,
)
from skimage.morphology.footprints import footprint_from_sequence
# Generate 2D and 3D structuring elements.
footprint_dict = {
"square 11x11 (separable)": (
footprint_rectangle((11, 11), decomposition=None),
footprint_rectangle((11, 11), decomposition="separable"),
),
"square 11x11 (sequence)": (
footprint_rectangle((11, 11), decomposition=None),
footprint_rectangle((11, 11), decomposition="sequence"),
),
"rectangle 7x11 (separable)": (
footprint_rectangle((7, 11), decomposition=None),
footprint_rectangle((7, 11), decomposition="separable"),
),
"rectangle 7x11 (sequence)": (
footprint_rectangle((7, 11), decomposition=None),
footprint_rectangle((7, 11), decomposition="sequence"),
),
"diamond(5) (sequence)": (
diamond(5, decomposition=None),
diamond(5, decomposition="sequence"),
),
"disk(7, strict_radius=False) (sequence)": (
disk(7, strict_radius=False, decomposition=None),
disk(7, strict_radius=False, decomposition="sequence"),
),
"disk(7, strict_radius=True) (crosses)": (
disk(7, strict_radius=True, decomposition=None),
disk(7, strict_radius=True, decomposition="crosses"),
),
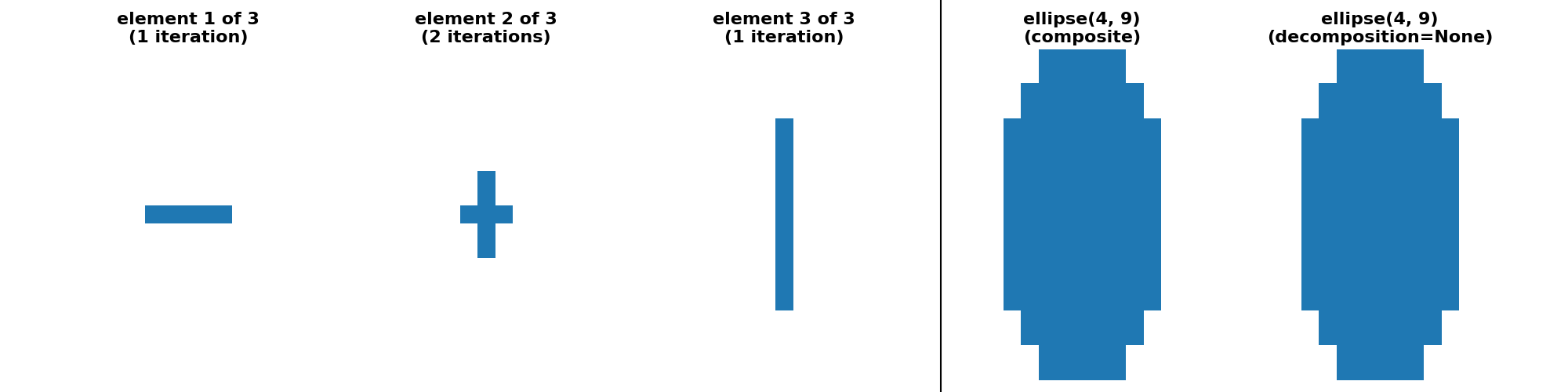
"ellipse(4, 9) (crosses)": (
ellipse(4, 9, decomposition=None),
ellipse(4, 9, decomposition="crosses"),
),
"disk(20) (sequence)": (
disk(20, strict_radius=False, decomposition=None),
disk(20, strict_radius=False, decomposition="sequence"),
),
"octagon(7, 4) (sequence)": (
octagon(7, 4, decomposition=None),
octagon(7, 4, decomposition="sequence"),
),
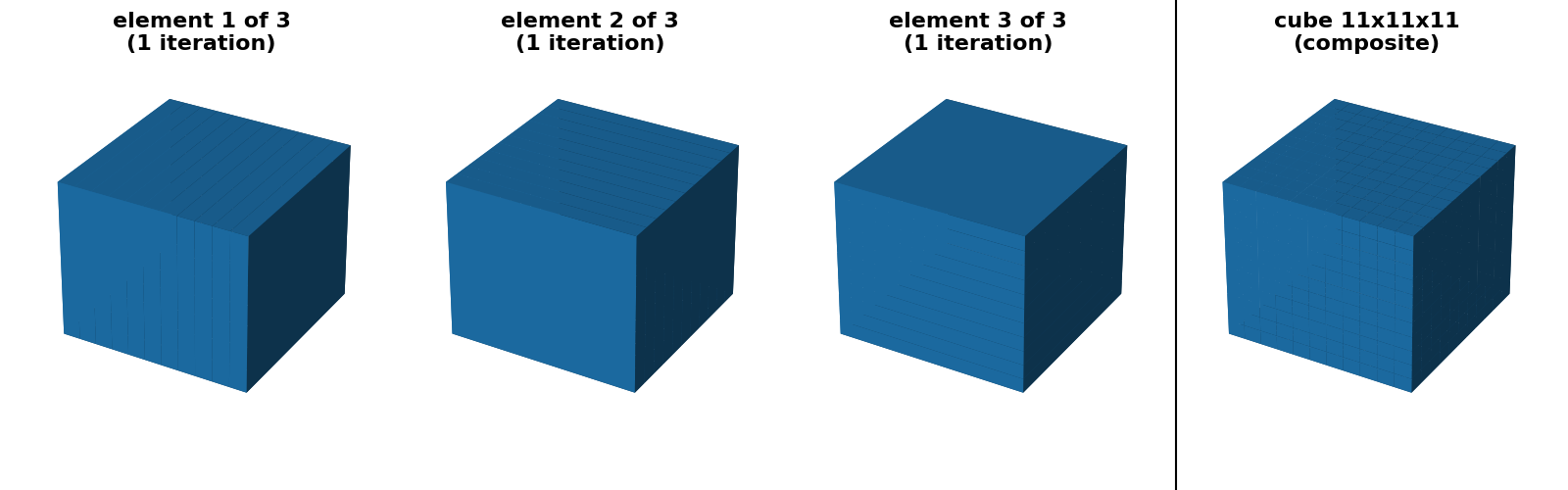
"cube 11x11x11 (separable)": (
footprint_rectangle((11, 11, 11), decomposition=None),
footprint_rectangle((11, 11, 11), decomposition="separable"),
),
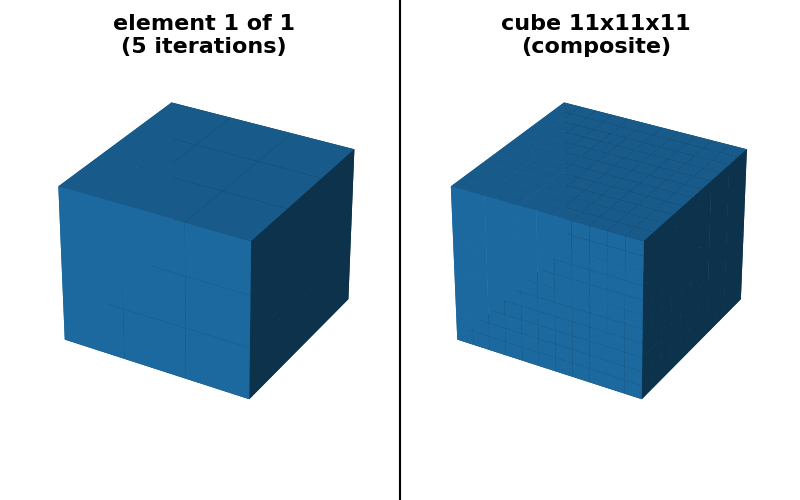
"cube 11x11x11 (sequence)": (
footprint_rectangle((11, 11, 11), decomposition=None),
footprint_rectangle((11, 11, 11), decomposition="sequence"),
),
"octahedron(7) (sequence)": (
octahedron(7, decomposition=None),
octahedron(7, decomposition="sequence"),
),
"ball(9) (sequence)": (
ball(9, strict_radius=False, decomposition=None),
ball(9, strict_radius=False, decomposition="sequence"),
),
}
# Visualize the elements
# binary white / blue colormap
cmap = colors.ListedColormap(['white', (0.1216, 0.4706, 0.70588)])
fontdict = dict(fontsize=16, fontweight='bold')
for title, (footprint, footprint_sequence) in footprint_dict.items():
ndim = footprint.ndim
num_seq = len(footprint_sequence)
approximate_decomposition = 'ball' in title or 'disk' in title or 'ellipse' in title
if approximate_decomposition:
# Two extra plot in approximate cases to show both:
# 1.) decomposition=None idea footprint
# 2.) actual composite footprint corresponding to the sequence
num_subplots = num_seq + 2
else:
# composite and decomposition=None are identical so only 1 extra plot
num_subplots = num_seq + 1
fig = plt.figure(figsize=(4 * num_subplots, 5))
if ndim == 2:
ax = fig.add_subplot(1, num_subplots, num_subplots)
ax.imshow(footprint, cmap=cmap, vmin=0, vmax=1)
if approximate_decomposition:
ax2 = fig.add_subplot(1, num_subplots, num_subplots - 1)
footprint_composite = footprint_from_sequence(footprint_sequence)
ax2.imshow(footprint_composite, cmap=cmap, vmin=0, vmax=1)
else:
ax = fig.add_subplot(1, num_subplots, num_subplots, projection=Axes3D.name)
ax.voxels(footprint, cmap=cmap)
if approximate_decomposition:
ax2 = fig.add_subplot(
1, num_subplots, num_subplots - 1, projection=Axes3D.name
)
footprint_composite = footprint_from_sequence(footprint_sequence)
ax2.voxels(footprint_composite, cmap=cmap)
title1 = title.split(' (')[0]
if approximate_decomposition:
# plot decomposition=None on a separate axis from the composite
title = title1 + '\n(decomposition=None)'
else:
# for exact cases composite and decomposition=None are identical
title = title1 + '\n(composite)'
ax.set_title(title, fontdict=fontdict)
ax.set_axis_off()
if approximate_decomposition:
ax2.set_title(title1 + '\n(composite)', fontdict=fontdict)
ax2.set_axis_off()
for n, (fp, num_reps) in enumerate(footprint_sequence):
npad = [((footprint.shape[d] - fp.shape[d]) // 2,) * 2 for d in range(ndim)]
fp = np.pad(fp, npad, mode='constant')
if ndim == 2:
ax = fig.add_subplot(1, num_subplots, n + 1)
ax.imshow(fp, cmap=cmap, vmin=0, vmax=1)
else:
ax = fig.add_subplot(1, num_subplots, n + 1, projection=Axes3D.name)
ax.voxels(fp, cmap=cmap)
title = f"element {n + 1} of {num_seq}\n({num_reps} iteration"
title += "s)" if num_reps > 1 else ")"
ax.set_title(title, fontdict=fontdict)
ax.set_axis_off()
ax.set_xlabel(f'num_reps = {num_reps}')
fig.tight_layout()
# draw a line separating the sequence elements from the composite
line_pos = num_seq / num_subplots
line = plt.Line2D([line_pos, line_pos], [0, 1], color="black")
fig.add_artist(line)
plt.show()
**スクリプトの実行合計時間:**(0分11.348秒)