画像への窓関数の適用

高速フーリエ変換（FFT）は、変換されるデータが周期信号の1周期を表していると仮定します。したがって、変換される信号の端点は、FFTのコンテキストでは不連続として振る舞う可能性があります。これらの不連続性はFFTの出力を歪め、「実在する」周波数成分のエネルギーがより広い周波数に漏洩するという結果になります。

スペクトルリークの影響は、信号に窓関数を掛けることで軽減できます。ウィンドウイングは、エッジに達するにつれて信号の振幅を滑らかに減衰させ、FFTによって生じる人工的な不連続性の影響を除去します。

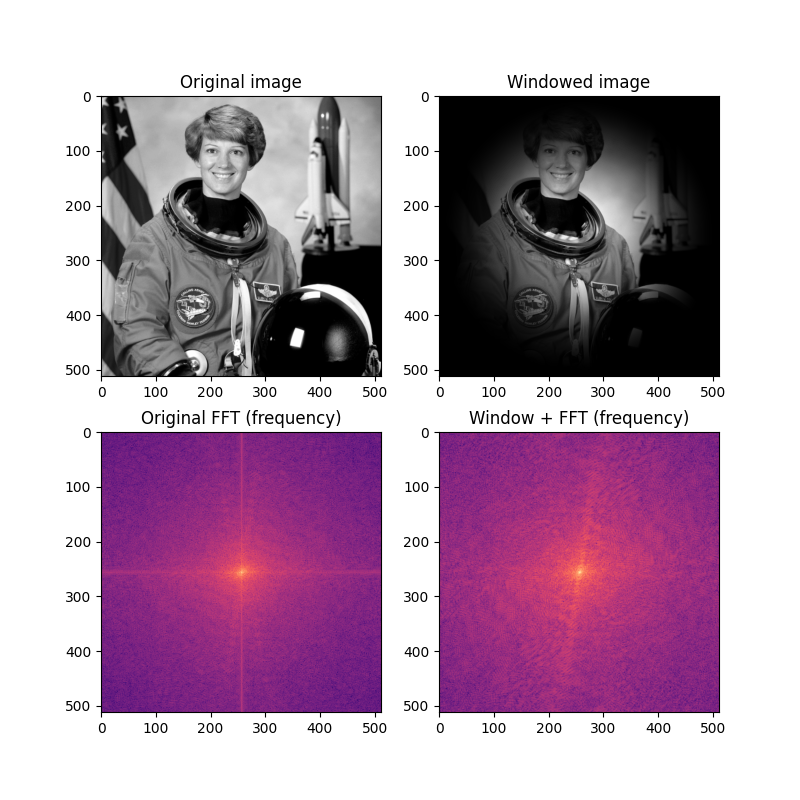
この例では、典型的な画像のFFTがx軸とy軸に沿って強いスペクトルリークを示すことがわかります（図の垂直線と水平線を参照）。2次元ハニング窓の適用は、スペクトルリークを大幅に削減し、FFTの周波数成分のプロットにおいて「実在する」周波数情報がより見やすくなります。

import matplotlib.pyplot as plt
import numpy as np
from scipy.fft import fft2, fftshift
from skimage import img_as_float
from skimage.color import rgb2gray
from skimage.data import astronaut
from skimage.filters import window

image = img_as_float(rgb2gray(astronaut()))

wimage = image * window('hann', image.shape)

image_f = np.abs(fftshift(fft2(image)))
wimage_f = np.abs(fftshift(fft2(wimage)))

fig, axes = plt.subplots(2, 2, figsize=(8, 8))
ax = axes.ravel()
ax[0].set_title("Original image")
ax[0].imshow(image, cmap='gray')
ax[1].set_title("Windowed image")
ax[1].imshow(wimage, cmap='gray')
ax[2].set_title("Original FFT (frequency)")
ax[2].imshow(np.log(image_f), cmap='magma')
ax[3].set_title("Window + FFT (frequency)")
ax[3].imshow(np.log(wimage_f), cmap='magma')
plt.show()