RANSACを使用したロバストな直線モデル推定

この例では、RANSAC（ランダムサンプルコンセンサス）アルゴリズムを使用して、 fehlerhaft なデータに直線モデルをロバストに適合させる方法を示します。

まず、線形関数にガウスノイズを追加することでデータを生成します。次に、外れ値の点がデータセットに追加されます。

RANSACは、データセットからパラメータを反復的に推定します。各反復で、次の手順が実行されます。

1. 元のデータからmin_samples個のランダムサンプルを選択し、データセットが有効かどうかを確認します（is_data_validオプションを参照）。

2. ランダムなサブセット（model_cls.estimate(*data[random_subset]）でモデルを推定し、推定されたモデルが有効かどうかを確認します（is_model_validオプションを参照）。

3. 推定されたモデル（model_cls.residuals(*data)）を使用して残差を計算することにより、すべてのデータポイントを内点または外れ値として分類します-residual_thresholdよりも小さい残差を持つすべてのデータサンプルは内点と見なされます。

4. 内点サンプルの数がこれまでよりも多い場合は、推定されたモデルを最良のモデルとして保存します。現在の推定モデルが同じ数の内点を持っている場合、残差の合計が小さい場合にのみ最良のモデルと見なされます。

これらの手順は、最大回数実行されるか、特別な停止基準のいずれかが満たされるまで実行されます。最終的なモデルは、以前に決定された最良のモデルのすべて内点サンプルを使用して推定されます。

import numpy as np
from matplotlib import pyplot as plt

from skimage.measure import LineModelND, ransac

rng = np.random.default_rng()

# generate coordinates of line
x = np.arange(-200, 200)
y = 0.2 * x + 20
data = np.column_stack([x, y])

# add gaussian noise to coordinates
noise = rng.normal(size=data.shape)
data += 0.5 * noise
data[::2] += 5 * noise[::2]
data[::4] += 20 * noise[::4]

# add faulty data
faulty = np.array(30 * [(180.0, -100)])
faulty += 10 * rng.normal(size=faulty.shape)
data[: faulty.shape[0]] = faulty

# fit line using all data
model = LineModelND()
model.estimate(data)

# robustly fit line only using inlier data with RANSAC algorithm
model_robust, inliers = ransac(
    data, LineModelND, min_samples=2, residual_threshold=1, max_trials=1000
)
outliers = inliers == False

# generate coordinates of estimated models
line_x = np.arange(-250, 250)
line_y = model.predict_y(line_x)
line_y_robust = model_robust.predict_y(line_x)

fig, ax = plt.subplots()
ax.plot(data[inliers, 0], data[inliers, 1], '.b', alpha=0.6, label='Inlier data')
ax.plot(data[outliers, 0], data[outliers, 1], '.r', alpha=0.6, label='Outlier data')
ax.plot(line_x, line_y, '-k', label='Line model from all data')
ax.plot(line_x, line_y_robust, '-b', label='Robust line model')
ax.legend(loc='lower left')
plt.show()

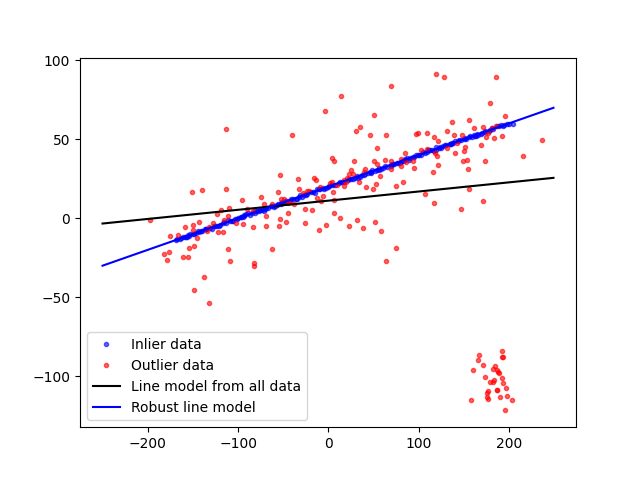
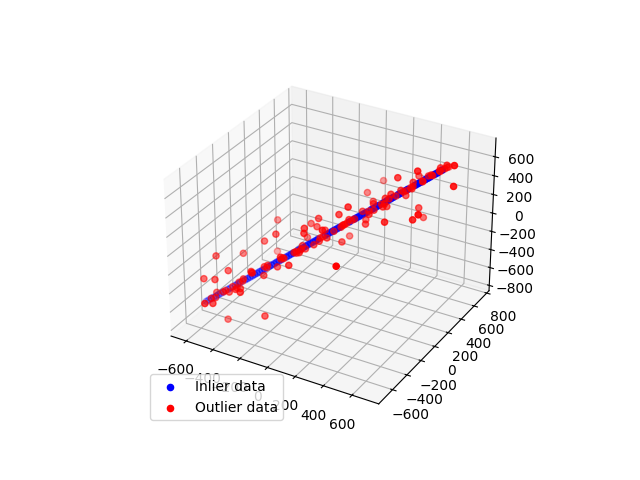
それでは、この例を3Dポイントに一般化します。

import numpy as np
from matplotlib import pyplot as plt
from skimage.measure import LineModelND, ransac


# generate coordinates of line
point = np.array([0, 0, 0], dtype='float')
direction = np.array([1, 1, 1], dtype='float') / np.sqrt(3)
xyz = point + 10 * np.arange(-100, 100)[..., np.newaxis] * direction

# add gaussian noise to coordinates
noise = rng.normal(size=xyz.shape)
xyz += 0.5 * noise
xyz[::2] += 20 * noise[::2]
xyz[::4] += 100 * noise[::4]

# robustly fit line only using inlier data with RANSAC algorithm
model_robust, inliers = ransac(
    xyz, LineModelND, min_samples=2, residual_threshold=1, max_trials=1000
)
outliers = inliers == False

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(
    xyz[inliers][:, 0],
    xyz[inliers][:, 1],
    xyz[inliers][:, 2],
    c='b',
    marker='o',
    label='Inlier data',
)
ax.scatter(
    xyz[outliers][:, 0],
    xyz[outliers][:, 1],
    xyz[outliers][:, 2],
    c='r',
    marker='o',
    label='Outlier data',
)
ax.legend(loc='lower left')
plt.show()