スケルトン化

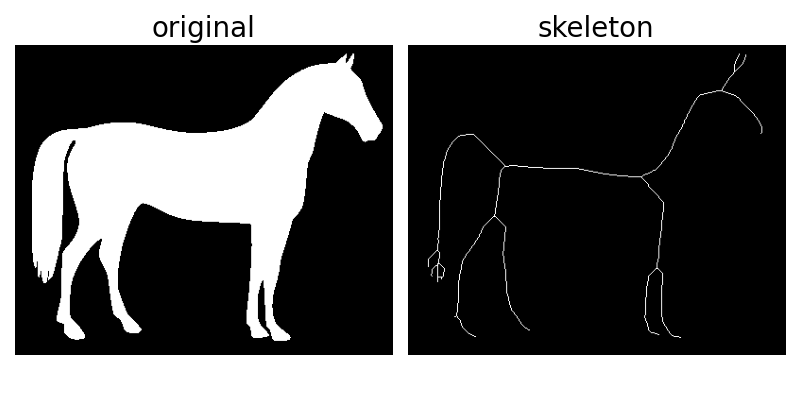
スケルトン化は、バイナリオブジェクトを1ピクセル幅の表現に縮小します。これは、特徴抽出やオブジェクトのトポロジの表現に役立ちます。

skeletonize は、画像を連続的に通過することで機能します。各パスで、対応するオブジェクトの接続性を損なわないという条件で、境界ピクセルが特定され、削除されます。

from skimage.morphology import skeletonize
from skimage import data
import matplotlib.pyplot as plt
from skimage.util import invert

# Invert the horse image
image = invert(data.horse())

# perform skeletonization
skeleton = skeletonize(image)

# display results
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(8, 4), sharex=True, sharey=True)

ax = axes.ravel()

ax[0].imshow(image, cmap=plt.cm.gray)
ax[0].axis('off')
ax[0].set_title('original', fontsize=20)

ax[1].imshow(skeleton, cmap=plt.cm.gray)
ax[1].axis('off')
ax[1].set_title('skeleton', fontsize=20)

fig.tight_layout()
plt.show()

張の方法と李の方法

skeletonize [Zha84] は、オブジェクトの境界にあるピクセルを削除する画像の連続的なパスを作成することによって機能します。これは、削除できるピクセルがなくなるまで続きます。画像は、8つの隣接ピクセルの可能なパターンに対応する範囲[0…255]の各ピクセルに数値を割り当てるマスクと相関しています。次に、ルックアップテーブルを使用して、ピクセルに0、1、2、または3の値を割り当てます。これは、反復中に選択的に削除されます。

skeletonize(..., method='lee') [Lee94] は、オクトツリーデータ構造を使用して、ピクセルの3x3x3近傍を調べます。アルゴリズムは、画像が変化しなくなるまで、反復ごとに画像をスイープし、各反復でピクセルを削除することで進行します。各反復は2つのステップで構成されます。最初に、削除候補のリストが作成されます。次に、画像の接続性をより適切に維持するために、このリストのピクセルが順番に再チェックされます。

李の方法 [Lee94] は3次元画像で使用するように設計されており、それらに対して自動的に選択されることに注意してください。説明のために、このアルゴリズムを2次元画像に適用します。

[Zha84]

デジタルパターンを間引くための高速並列アルゴリズム、T. Y. ZhangおよびC. Y. Suen、Communications of the ACM、1984年3月、Volume 27、Number 3。

[Lee94] (1,2)

T.-C. Lee、R.L. Kashyap、およびC.-N. Chu、3次元メディアルサーフェス/軸間引きアルゴリズムによるスケルトンモデルの構築。コンピュータービジョン、グラフィックス、および画像処理、56（6）：462-478、1994。

import matplotlib.pyplot as plt
from skimage.morphology import skeletonize

blobs = data.binary_blobs(200, blob_size_fraction=0.2, volume_fraction=0.35, rng=1)

skeleton = skeletonize(blobs)
skeleton_lee = skeletonize(blobs, method='lee')

fig, axes = plt.subplots(1, 3, figsize=(8, 4), sharex=True, sharey=True)
ax = axes.ravel()

ax[0].imshow(blobs, cmap=plt.cm.gray)
ax[0].set_title('original')
ax[0].axis('off')

ax[1].imshow(skeleton, cmap=plt.cm.gray)
ax[1].set_title('skeletonize')
ax[1].axis('off')

ax[2].imshow(skeleton_lee, cmap=plt.cm.gray)
ax[2].set_title('skeletonize (Lee 94)')
ax[2].axis('off')

fig.tight_layout()
plt.show()

メディアル軸スケルトン化

オブジェクトのメディアル軸は、オブジェクトの境界上に複数の最近傍点を持つすべての点の集合です。これは、元のオブジェクトと同じ接続性を持つオブジェクトの1ピクセル幅のスケルトンであるため、トポロジカルスケルトンと呼ばれることがよくあります。

ここでは、メディアル軸変換を使用して、前景オブジェクトの幅を計算します。medial_axis 関数は、メディアル軸に加えて距離変換（キーワード引数 return_distance=True を使用）を返すため、この関数を使用して、メディアル軸のすべての点の背景までの距離を計算できます。これにより、オブジェクトのローカル幅の推定値が得られます。

ブランチが少ないスケルトンについては、skeletonize を優先する必要があります。

from skimage.morphology import medial_axis, skeletonize

# Generate the data
blobs = data.binary_blobs(200, blob_size_fraction=0.2, volume_fraction=0.35, rng=1)

# Compute the medial axis (skeleton) and the distance transform
skel, distance = medial_axis(blobs, return_distance=True)

# Compare with other skeletonization algorithms
skeleton = skeletonize(blobs)
skeleton_lee = skeletonize(blobs, method='lee')

# Distance to the background for pixels of the skeleton
dist_on_skel = distance * skel

fig, axes = plt.subplots(2, 2, figsize=(8, 8), sharex=True, sharey=True)
ax = axes.ravel()

ax[0].imshow(blobs, cmap=plt.cm.gray)
ax[0].set_title('original')
ax[0].axis('off')

ax[1].imshow(dist_on_skel, cmap='magma')
ax[1].contour(blobs, [0.5], colors='w')
ax[1].set_title('medial_axis')
ax[1].axis('off')

ax[2].imshow(skeleton, cmap=plt.cm.gray)
ax[2].set_title('skeletonize')
ax[2].axis('off')

ax[3].imshow(skeleton_lee, cmap=plt.cm.gray)
ax[3].set_title("skeletonize (Lee 94)")
ax[3].axis('off')

fig.tight_layout()
plt.show()

モルフォロジカル間引き

thin 関数に実装されているモルフォロジカル間引きは、skeletonize と同じ原理で動作します。接続性を変更することなく削除できなくなるまで、各反復で境界からピクセルを削除します。異なる削除ルールにより、スケルトン化を高速化し、異なる最終スケルトンが得られる可能性があります。

thin 関数には、間引きの反復回数を制限し、比較的厚いスケルトンを生成するためのオプションの max_num_iter キーワード引数もあります。

from skimage.morphology import skeletonize, thin

skeleton = skeletonize(image)
thinned = thin(image)
thinned_partial = thin(image, max_num_iter=25)

fig, axes = plt.subplots(2, 2, figsize=(8, 8), sharex=True, sharey=True)
ax = axes.ravel()

ax[0].imshow(image, cmap=plt.cm.gray)
ax[0].set_title('original')
ax[0].axis('off')

ax[1].imshow(skeleton, cmap=plt.cm.gray)
ax[1].set_title('skeleton')
ax[1].axis('off')

ax[2].imshow(thinned, cmap=plt.cm.gray)
ax[2].set_title('thinned')
ax[2].axis('off')

ax[3].imshow(thinned_partial, cmap=plt.cm.gray)
ax[3].set_title('partially thinned')
ax[3].axis('off')

fig.tight_layout()
plt.show()