ランクフィルター

ランクフィルターは、局所的なグレースケール順序を使用してフィルタリングされた値を計算する非線形フィルターです。このフィルター群は、共通の基盤を共有しています。局所的なグレースケールヒストグラムは、ピクセルの近傍（2D構造要素で定義される）で計算されます。フィルタリングされた値がヒストグラムの中央値として取得される場合、古典的なメディアンフィルターが得られます。

ランクフィルターは、次のようなさまざまな目的で使用できます。

• 画像品質の向上（例：画像の平滑化、シャープ化）

• 画像の前処理（例：ノイズ除去、コントラスト強調）

• 特徴抽出（例：境界検出、孤立点検出）

• 画像の後処理（例：小さなオブジェクトの除去、オブジェクトのグループ化、輪郭の平滑化）

一部のよく知られたフィルター（例：モルフォロジー膨張およびモルフォロジー侵食）は、ランクフィルターの特定の場合です[1]。

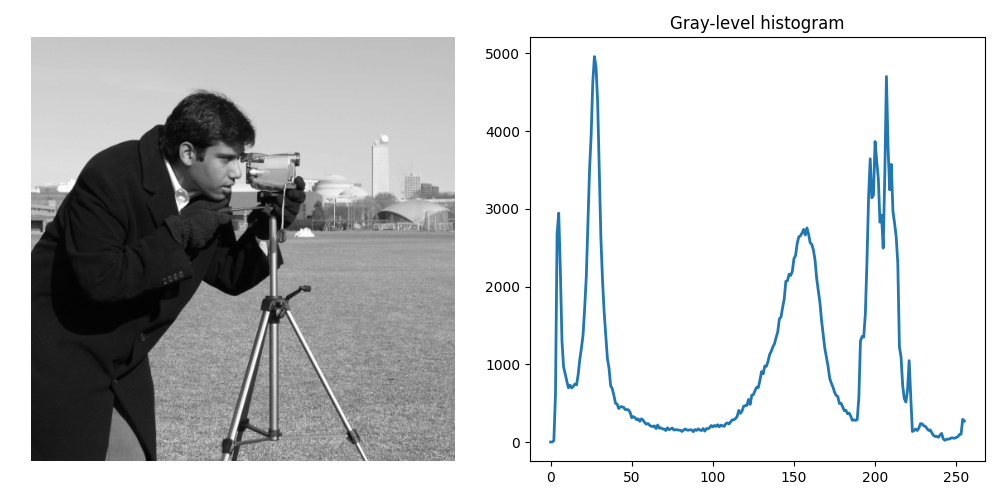
この例では、skimageで利用可能な線形および非線形フィルターを使用してグレースケール画像をフィルタリングする方法を見ていきます。すべての比較に、skimage.dataのcamera画像を使用します。

[1]

Pierre Soille, On morphological operators based on rank filters, Pattern Recognition 35 (2002) 527-535, DOI:10.1016/S0031-3203(01)00047-4

import numpy as np
import matplotlib.pyplot as plt

from skimage.util import img_as_ubyte
from skimage import data
from skimage.exposure import histogram

noisy_image = img_as_ubyte(data.camera())
hist, hist_centers = histogram(noisy_image)

fig, ax = plt.subplots(ncols=2, figsize=(10, 5))

ax[0].imshow(noisy_image, cmap=plt.cm.gray)
ax[0].set_axis_off()

ax[1].plot(hist_centers, hist, lw=2)
ax[1].set_title('Gray-level histogram')

fig.tight_layout()

ノイズ除去

画像にいくつかのノイズが追加されます。ピクセルの1％がランダムに255に設定され、1％がランダムに0に設定されます。ノイズを除去するために、メディアンフィルターが適用されます。

from skimage.filters.rank import median
from skimage.morphology import disk, ball

rng = np.random.default_rng()
noise = rng.random(noisy_image.shape)
noisy_image = img_as_ubyte(data.camera())
noisy_image[noise > 0.99] = 255
noisy_image[noise < 0.01] = 0

fig, axes = plt.subplots(2, 2, figsize=(10, 10), sharex=True, sharey=True)
ax = axes.ravel()

ax[0].imshow(noisy_image, vmin=0, vmax=255, cmap=plt.cm.gray)
ax[0].set_title('Noisy image')

ax[1].imshow(median(noisy_image, disk(1)), vmin=0, vmax=255, cmap=plt.cm.gray)
ax[1].set_title('Median $r=1$')

ax[2].imshow(median(noisy_image, disk(5)), vmin=0, vmax=255, cmap=plt.cm.gray)
ax[2].set_title('Median $r=5$')

ax[3].imshow(median(noisy_image, disk(20)), vmin=0, vmax=255, cmap=plt.cm.gray)
ax[3].set_title('Median $r=20$')

for a in ax:
    a.set_axis_off()

fig.tight_layout()

追加されたノイズは、画像のデフォルトが小さい（1ピクセル幅）ため、効率的に除去されます。小さなフィルター半径で十分です。半径が増加するにつれて、カメラの三脚など、より大きなサイズのオブジェクトもフィルタリングされます。メディアンフィルターは、境界を保持するため、ノイズ除去によく使用されます。たとえば、塩コショウノイズ[2]のように、画像全体のごく一部のピクセルにのみノイズがある場合を考えてみましょう。メディアンフィルターは、ノイズの多いピクセルを外れ値として無視するため、移動平均フィルターとは対照的に、局所的なピクセルグループの中央値を大きく変えることはありません。

[2]

https://en.wikipedia.org/wiki/Salt-and-pepper_noise

画像の平滑化

以下の例では、局所的な平均フィルターがカメラマンの画像を平滑化する方法を示しています。

from skimage.filters.rank import mean

loc_mean = mean(noisy_image, disk(10))

fig, ax = plt.subplots(ncols=2, figsize=(10, 5), sharex=True, sharey=True)

ax[0].imshow(noisy_image, vmin=0, vmax=255, cmap=plt.cm.gray)
ax[0].set_title('Original')

ax[1].imshow(loc_mean, vmin=0, vmax=255, cmap=plt.cm.gray)
ax[1].set_title('Local mean $r=10$')

for a in ax:
    a.set_axis_off()

fig.tight_layout()

重要な境界を保持しながら画像を平滑化することに関心があるかもしれません（メディアンフィルターはすでにこれを実現しています）。ここでは、局所的な近傍を中央のものと同様のグレースケールを持つピクセルに制限するバイラテラルフィルターを使用します。

注意

skimage.restoration.denoise_bilateral()では、カラー画像に対して異なる実装が利用可能です。

from skimage.filters.rank import mean_bilateral

noisy_image = img_as_ubyte(data.camera())

bilat = mean_bilateral(noisy_image.astype(np.uint16), disk(20), s0=10, s1=10)

fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(10, 10), sharex='row', sharey='row')
ax = axes.ravel()

ax[0].imshow(noisy_image, cmap=plt.cm.gray)
ax[0].set_title('Original')

ax[1].imshow(bilat, cmap=plt.cm.gray)
ax[1].set_title('Bilateral mean')

ax[2].imshow(noisy_image[100:250, 350:450], cmap=plt.cm.gray)

ax[3].imshow(bilat[100:250, 350:450], cmap=plt.cm.gray)

for a in ax:
    a.set_axis_off()

fig.tight_layout()

画像（例：空）の大きな連続部分は平滑化され、その他の詳細は保持されていることがわかります。

コントラスト強調

ここでは、グローバルヒストグラム平坦化が局所的にどのように適用されるかを比較します。

平坦化された画像[3]は、各ピクセルの近傍に対してほぼ線形の累積分布関数を持っています。ヒストグラム平坦化の局所バージョン[4]は、すべての局所的なグレースケールの変化を強調します。

[3]

https://en.wikipedia.org/wiki/Histogram_equalization

[4]

https://en.wikipedia.org/wiki/Adaptive_histogram_equalization

from skimage import exposure
from skimage.filters import rank

noisy_image = img_as_ubyte(data.camera())

# equalize globally and locally
glob = exposure.equalize_hist(noisy_image) * 255
loc = rank.equalize(noisy_image, disk(20))

# extract histogram for each image
hist = np.histogram(noisy_image, bins=np.arange(0, 256))
glob_hist = np.histogram(glob, bins=np.arange(0, 256))
loc_hist = np.histogram(loc, bins=np.arange(0, 256))

fig, axes = plt.subplots(nrows=3, ncols=2, figsize=(12, 12))
ax = axes.ravel()

ax[0].imshow(noisy_image, cmap=plt.cm.gray)
ax[0].set_axis_off()

ax[1].plot(hist[1][:-1], hist[0], lw=2)
ax[1].set_title('Histogram of gray values')

ax[2].imshow(glob, cmap=plt.cm.gray)
ax[2].set_axis_off()

ax[3].plot(glob_hist[1][:-1], glob_hist[0], lw=2)
ax[3].set_title('Histogram of gray values')

ax[4].imshow(loc, cmap=plt.cm.gray)
ax[4].set_axis_off()

ax[5].plot(loc_hist[1][:-1], loc_hist[0], lw=2)
ax[5].set_title('Histogram of gray values')

fig.tight_layout()

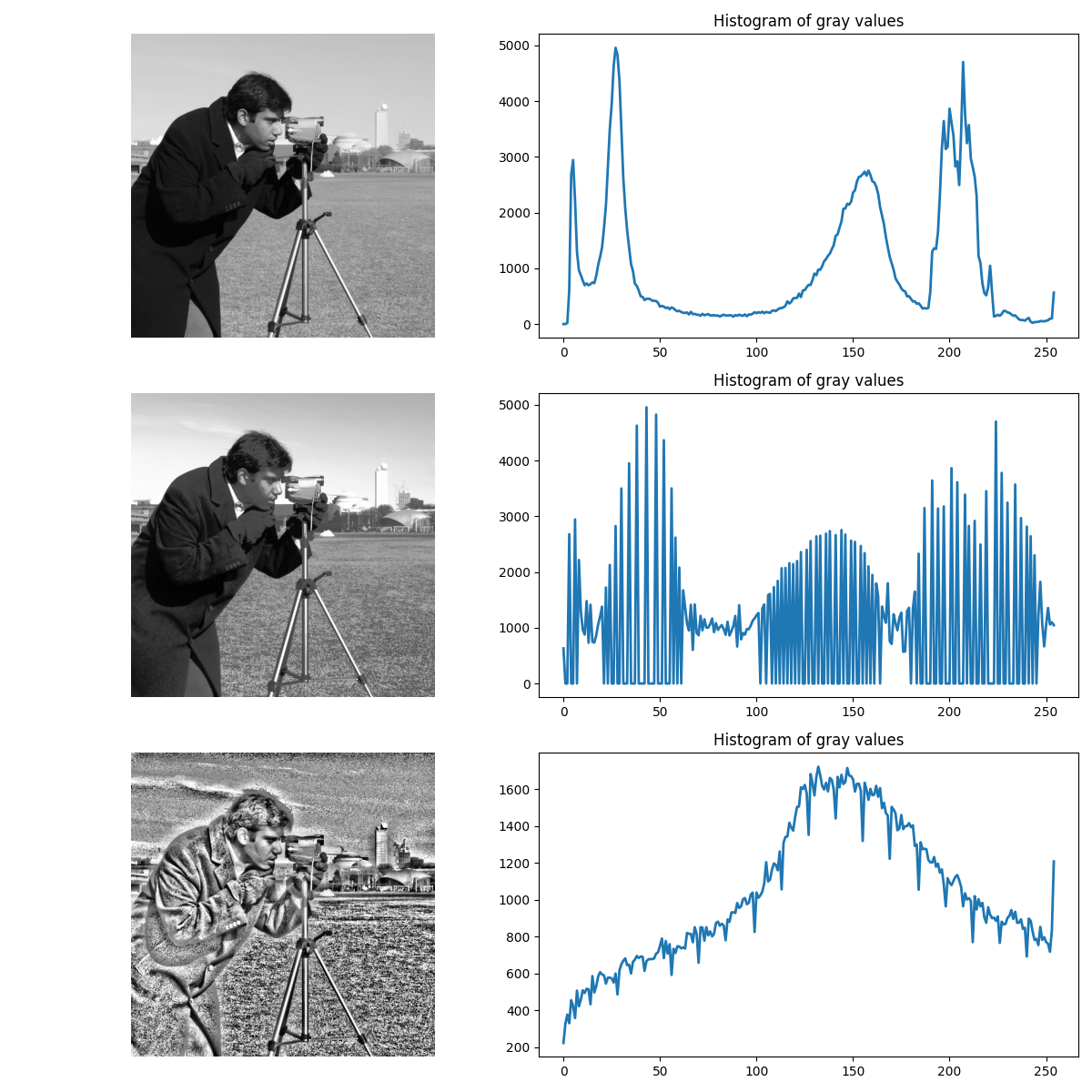
画像に使用されるグレースケールの数を最大化するもう1つの方法は、局所的な自動レベル調整を適用することです。つまり、ピクセルのグレースケール値が局所的な最小値と局所的な最大値の間で比例的に再マッピングされます。

次の例では、局所的な自動レベル調整によってカメラマンの画像がどのように強化されるかを示します。

from skimage.filters.rank import autolevel

noisy_image = img_as_ubyte(data.camera())

auto = autolevel(noisy_image.astype(np.uint16), disk(20))

fig, ax = plt.subplots(ncols=2, figsize=(10, 5), sharex=True, sharey=True)

ax[0].imshow(noisy_image, cmap=plt.cm.gray)
ax[0].set_title('Original')

ax[1].imshow(auto, cmap=plt.cm.gray)
ax[1].set_title('Local autolevel')

for a in ax:
    a.set_axis_off()

fig.tight_layout()

このフィルターは、局所的な外れ値に非常に敏感です。局所的な最小値と最大値の代わりに特定のパーセンタイル（下位パーセンタイルと上位パーセンタイル）を使用する、自動レベルフィルターのパーセンタイルバージョンを使用してこれを緩和できます。以下の例では、パーセンタイルパラメーターが局所的な自動レベルの結果にどのように影響するかを示しています。

from skimage.filters.rank import autolevel_percentile

image = data.camera()

footprint = disk(20)
loc_autolevel = autolevel(image, footprint=footprint)
loc_perc_autolevel0 = autolevel_percentile(image, footprint=footprint, p0=0.01, p1=0.99)
loc_perc_autolevel1 = autolevel_percentile(image, footprint=footprint, p0=0.05, p1=0.95)
loc_perc_autolevel2 = autolevel_percentile(image, footprint=footprint, p0=0.1, p1=0.9)
loc_perc_autolevel3 = autolevel_percentile(image, footprint=footprint, p0=0.15, p1=0.85)

fig, axes = plt.subplots(nrows=3, ncols=2, figsize=(10, 10), sharex=True, sharey=True)
ax = axes.ravel()

title_list = [
    'Original',
    'auto_level',
    'auto-level 1%',
    'auto-level 5%',
    'auto-level 10%',
    'auto-level 15%',
]
image_list = [
    image,
    loc_autolevel,
    loc_perc_autolevel0,
    loc_perc_autolevel1,
    loc_perc_autolevel2,
    loc_perc_autolevel3,
]

for i in range(0, len(image_list)):
    ax[i].imshow(image_list[i], cmap=plt.cm.gray, vmin=0, vmax=255)
    ax[i].set_title(title_list[i])
    ax[i].set_axis_off()

fig.tight_layout()

モルフォロジーコントラスト強調フィルターは、元のピクセル値が局所的な最大値に最も近い場合は中央ピクセルを局所的な最大値に置き換え、それ以外の場合は最小値に置き換えます。

from skimage.filters.rank import enhance_contrast

noisy_image = img_as_ubyte(data.camera())

enh = enhance_contrast(noisy_image, disk(5))

fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(10, 10), sharex='row', sharey='row')
ax = axes.ravel()

ax[0].imshow(noisy_image, cmap=plt.cm.gray)
ax[0].set_title('Original')

ax[1].imshow(enh, cmap=plt.cm.gray)
ax[1].set_title('Local morphological contrast enhancement')

ax[2].imshow(noisy_image[100:250, 350:450], cmap=plt.cm.gray)

ax[3].imshow(enh[100:250, 350:450], cmap=plt.cm.gray)

for a in ax:
    a.set_axis_off()

fig.tight_layout()

局所的なモルフォロジーコントラスト強調のパーセンタイルバージョンでは、局所的な最小値と最大値の代わりにパーセンタイルp0とp1を使用します。

from skimage.filters.rank import enhance_contrast_percentile

noisy_image = img_as_ubyte(data.camera())

penh = enhance_contrast_percentile(noisy_image, disk(5), p0=0.1, p1=0.9)

fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(10, 10), sharex='row', sharey='row')
ax = axes.ravel()

ax[0].imshow(noisy_image, cmap=plt.cm.gray)
ax[0].set_title('Original')

ax[1].imshow(penh, cmap=plt.cm.gray)
ax[1].set_title('Local percentile morphological\n contrast enhancement')

ax[2].imshow(noisy_image[100:250, 350:450], cmap=plt.cm.gray)

ax[3].imshow(penh[100:250, 350:450], cmap=plt.cm.gray)

for a in ax:
    a.set_axis_off()

fig.tight_layout()

画像閾値

大津の閾値処理法[5]は、局所的なグレースケール分布を使用して局所的に適用できます。以下の例では、各ピクセルについて、構造要素によって定義された局所近傍の2つのピクセルクラス間の分散を最大化することによって「最適な」閾値が決定されます。

これらのアルゴリズムは、2D画像と3D画像のどちらにも使用できます。

この例では、skimage.filters.threshold_otsu()によって提供されるグローバル閾値処理と局所閾値処理を比較します。前者は後者よりもはるかに遅いことに注意してください。

[5]

https://en.wikipedia.org/wiki/Otsu’s_method

from skimage.filters.rank import otsu
from skimage.filters import threshold_otsu
from skimage import exposure

p8 = data.page()

radius = 10
footprint = disk(radius)

# t_loc_otsu is an image
t_loc_otsu = otsu(p8, footprint)
loc_otsu = p8 >= t_loc_otsu

# t_glob_otsu is a scalar
t_glob_otsu = threshold_otsu(p8)
glob_otsu = p8 >= t_glob_otsu

fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(12, 12), sharex=True, sharey=True)
ax = axes.ravel()

fig.colorbar(ax[0].imshow(p8, cmap=plt.cm.gray), ax=ax[0])
ax[0].set_title('Original')

fig.colorbar(ax[1].imshow(t_loc_otsu, cmap=plt.cm.gray), ax=ax[1])
ax[1].set_title(f'Local Otsu ($r={radius}$)')

ax[2].imshow(p8 >= t_loc_otsu, cmap=plt.cm.gray)
ax[2].set_title('Original >= local Otsu')

ax[3].imshow(glob_otsu, cmap=plt.cm.gray)
ax[3].set_title(f'Global Otsu ($t={t_glob_otsu}$)')

for a in ax:
    a.set_axis_off()

fig.tight_layout()

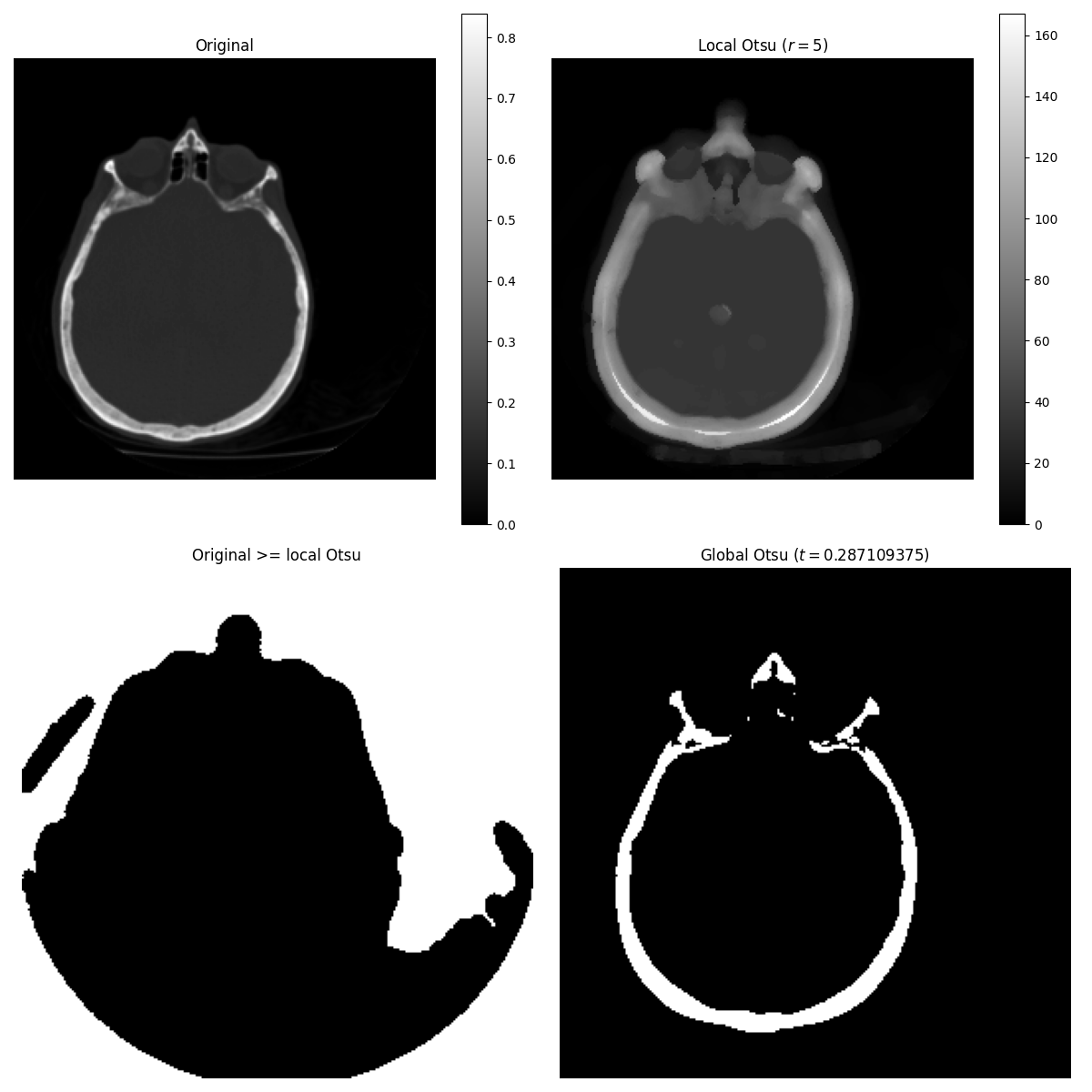
以下の例では、今回は3D画像を使用して同じ比較を実行します。

brain = exposure.rescale_intensity(data.brain().astype(float))

radius = 5
neighborhood = ball(radius)

# t_loc_otsu is an image
t_loc_otsu = rank.otsu(brain, neighborhood)
loc_otsu = brain >= t_loc_otsu

# t_glob_otsu is a scalar
t_glob_otsu = threshold_otsu(brain)
glob_otsu = brain >= t_glob_otsu

fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(12, 12), sharex=True, sharey=True)
ax = axes.ravel()

slice_index = 3

fig.colorbar(ax[0].imshow(brain[slice_index], cmap=plt.cm.gray), ax=ax[0])
ax[0].set_title('Original')

fig.colorbar(ax[1].imshow(t_loc_otsu[slice_index], cmap=plt.cm.gray), ax=ax[1])
ax[1].set_title(f'Local Otsu ($r={radius}$)')

ax[2].imshow(brain[slice_index] >= t_loc_otsu[slice_index], cmap=plt.cm.gray)
ax[2].set_title('Original >= local Otsu')

ax[3].imshow(glob_otsu[slice_index], cmap=plt.cm.gray)
ax[3].set_title(f'Global Otsu ($t={t_glob_otsu}$)')

for a in ax:
    a.set_axis_off()

fig.tight_layout()

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/skimage/filters/rank/generic.py:353: UserWarning:

Possible precision loss converting image of type float64 to uint8 as required by rank filters. Convert manually using skimage.util.img_as_ubyte to silence this warning.

次の例では、合成画像に適用されたグローバルレベルシフトを局所的な大津閾値処理がどのように処理するかを示します。

n = 100
theta = np.linspace(0, 10 * np.pi, n)
x = np.sin(theta)
m = (np.tile(x, (n, 1)) * np.linspace(0.1, 1, n) * 128 + 128).astype(np.uint8)

radius = 10
t = rank.otsu(m, disk(radius))

fig, ax = plt.subplots(ncols=2, figsize=(10, 5), sharex=True, sharey=True)

ax[0].imshow(m, cmap=plt.cm.gray)
ax[0].set_title('Original')

ax[1].imshow(m >= t, cmap=plt.cm.gray)
ax[1].set_title(f'Local Otsu ($r={radius}$)')

for a in ax:
    a.set_axis_off()

fig.tight_layout()

画像モルフォロジー

局所最大値と局所最小値は、グレースケールモルフォロジーの基本演算子です。

これは、古典的なモルフォロジーグレースケールフィルターの例です。opening、closing、およびモルフォロジー勾配です。

from skimage.filters.rank import maximum, minimum, gradient

noisy_image = img_as_ubyte(data.camera())

opening = maximum(minimum(noisy_image, disk(5)), disk(5))
closing = minimum(maximum(noisy_image, disk(5)), disk(5))
grad = gradient(noisy_image, disk(5))

# display results
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(10, 10), sharex=True, sharey=True)
ax = axes.ravel()

ax[0].imshow(noisy_image, cmap=plt.cm.gray)
ax[0].set_title('Original')

ax[1].imshow(closing, cmap=plt.cm.gray)
ax[1].set_title('Gray-level closing')

ax[2].imshow(opening, cmap=plt.cm.gray)
ax[2].set_title('Gray-level opening')

ax[3].imshow(grad, cmap=plt.cm.gray)
ax[3].set_title('Morphological gradient')

for a in ax:
    a.set_axis_off()

fig.tight_layout()

特徴抽出

局所ヒストグラムを利用して、局所エントロピーを計算できます。これは局所的な画像の複雑さに関連しています。エントロピーは底を2とする対数を用いて計算されます。すなわち、このフィルターは、局所的なグレースケール分布をエンコードするために必要な最小ビット数を返します。

skimage.filters.rank.entropy()は、与えられた構造要素における局所エントロピーを返します。次の例では、このフィルターを8ビットと16ビットの画像に適用しています。

注意

利用可能な画像ビットをより有効に活用するため、この関数は8ビット画像に対してはエントロピーを10倍に、16ビット画像に対してはエントロピーを1000倍にして返します。

from skimage import data
from skimage.filters.rank import entropy
from skimage.morphology import disk
import numpy as np
import matplotlib.pyplot as plt

image = data.camera()

fig, ax = plt.subplots(ncols=2, figsize=(12, 6), sharex=True, sharey=True)

fig.colorbar(ax[0].imshow(image, cmap=plt.cm.gray), ax=ax[0])
ax[0].set_title('Image')

fig.colorbar(ax[1].imshow(entropy(image, disk(5)), cmap=plt.cm.gray), ax=ax[1])
ax[1].set_title('Entropy')

for a in ax:
    a.set_axis_off()

fig.tight_layout()

実装

skimage.filters.rankフィルターの中核部分は、局所的なグレースケールヒストグラムを更新するスライディングウィンドウに基づいて構築されています。このアプローチにより、アルゴリズムの複雑さはO(n)に制限されます。ここで、nは画像ピクセル数です。複雑さは構造要素のサイズに関しても制限されます。

以下では、skimageで利用可能なさまざまな実装のパフォーマンスを比較します。

from time import time

from scipy.ndimage import percentile_filter
from skimage.morphology import dilation
from skimage.filters.rank import median, maximum


def exec_and_timeit(func):
    """Decorator that returns both function results and execution time."""

    def wrapper(*arg):
        t1 = time()
        res = func(*arg)
        t2 = time()
        ms = (t2 - t1) * 1000.0
        return (res, ms)

    return wrapper


@exec_and_timeit
def cr_med(image, footprint):
    return median(image=image, footprint=footprint)


@exec_and_timeit
def cr_max(image, footprint):
    return maximum(image=image, footprint=footprint)


@exec_and_timeit
def cm_dil(image, footprint):
    return dilation(image=image, footprint=footprint)


@exec_and_timeit
def ndi_med(image, n):
    return percentile_filter(image, 50, size=n * 2 - 1)

比較対象:

• skimage.filters.rank.maximum

• skimage.morphology.dilation

構造要素サイズの増加に伴う比較

a = data.camera()

rec = []
e_range = range(1, 20, 2)
for r in e_range:
    elem = disk(r + 1)
    rc, ms_rc = cr_max(a, elem)
    rcm, ms_rcm = cm_dil(a, elem)
    rec.append((ms_rc, ms_rcm))

rec = np.asarray(rec)

fig, ax = plt.subplots(figsize=(10, 10), sharey=True)
ax.set_title('Performance with respect to element size')
ax.set_ylabel('Time (ms)')
ax.set_xlabel('Element radius')
ax.plot(e_range, rec)
ax.legend(['filters.rank.maximum', 'morphology.dilate'])

fig.tight_layout()

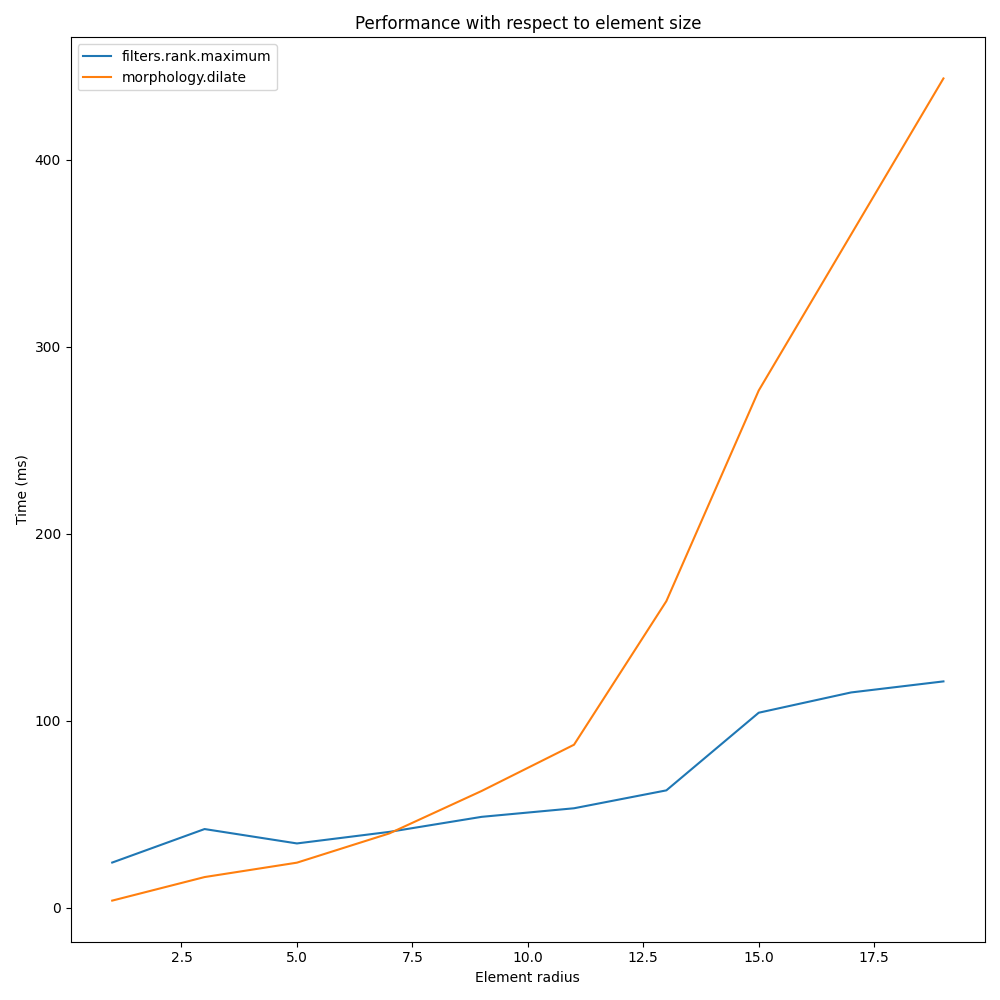
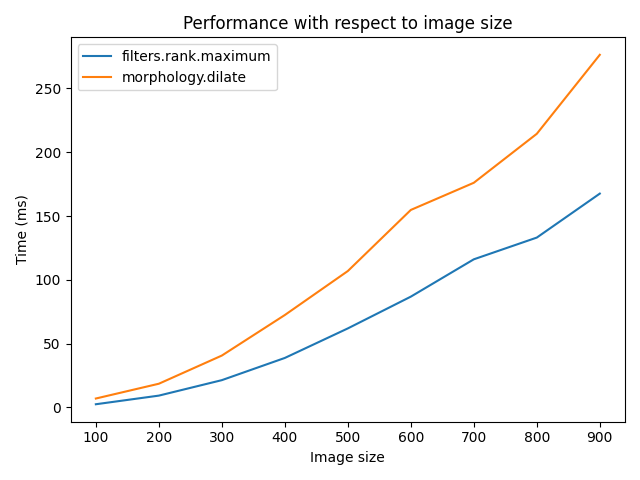
画像サイズの増加に伴う比較

r = 9
elem = disk(r + 1)

rec = []
s_range = range(100, 1000, 100)
for s in s_range:
    a = (rng.random((s, s)) * 256).astype(np.uint8)
    (rc, ms_rc) = cr_max(a, elem)
    (rcm, ms_rcm) = cm_dil(a, elem)
    rec.append((ms_rc, ms_rcm))

rec = np.asarray(rec)

fig, ax = plt.subplots()
ax.set_title('Performance with respect to image size')
ax.set_ylabel('Time (ms)')
ax.set_xlabel('Image size')
ax.plot(s_range, rec)
ax.legend(['filters.rank.maximum', 'morphology.dilate'])

fig.tight_layout()

比較対象:

• skimage.filters.rank.median

• scipy.ndimage.percentile_filter

構造要素サイズの増加に伴う比較

a = data.camera()

rec = []
e_range = range(2, 30, 4)
for r in e_range:
    elem = disk(r + 1)
    rc, ms_rc = cr_med(a, elem)
    rndi, ms_ndi = ndi_med(a, r)
    rec.append((ms_rc, ms_ndi))

rec = np.asarray(rec)

fig, ax = plt.subplots()
ax.set_title('Performance with respect to element size')
ax.plot(e_range, rec)
ax.legend(['filters.rank.median', 'scipy.ndimage.percentile'])
ax.set_ylabel('Time (ms)')
ax.set_xlabel('Element radius')

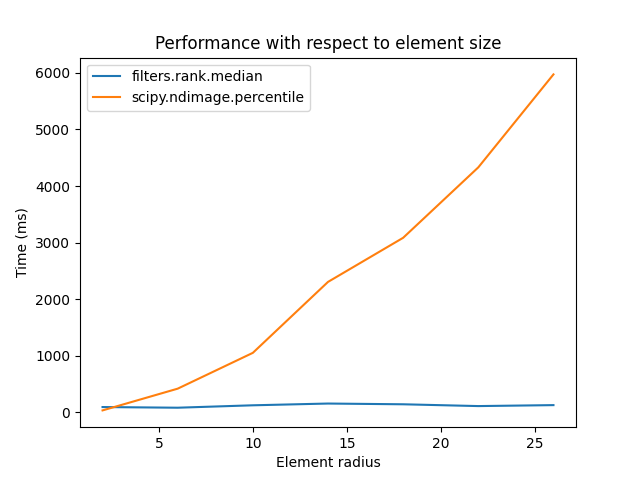
Text(0.5, 23.52222222222222, 'Element radius')

2つの手法の結果の比較

fig, ax = plt.subplots(ncols=2, figsize=(10, 5), sharex=True, sharey=True)

ax[0].set_title('filters.rank.median')
ax[0].imshow(rc, cmap=plt.cm.gray)

ax[1].set_title('scipy.ndimage.percentile')
ax[1].imshow(rndi, cmap=plt.cm.gray)

for a in ax:
    a.set_axis_off()

fig.tight_layout()

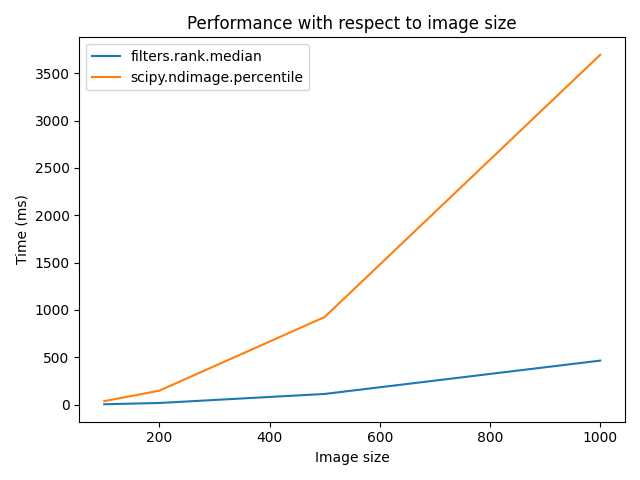
画像サイズの増加に伴う比較

r = 9
elem = disk(r + 1)

rec = []
s_range = [100, 200, 500, 1000]
for s in s_range:
    a = (rng.random((s, s)) * 256).astype(np.uint8)
    (rc, ms_rc) = cr_med(a, elem)
    rndi, ms_ndi = ndi_med(a, r)
    rec.append((ms_rc, ms_ndi))

rec = np.asarray(rec)

fig, ax = plt.subplots()
ax.set_title('Performance with respect to image size')
ax.plot(s_range, rec)
ax.legend(['filters.rank.median', 'scipy.ndimage.percentile'])
ax.set_ylabel('Time (ms)')
ax.set_xlabel('Image size')

fig.tight_layout()

plt.show()