ぼかしの強さの推定

この例では、`measure.blur_effect` に実装されているメトリックが、ぼかしの強さと再ぼかしフィルターのサイズの両方の関数としてどのように動作するかを示します。このノンリファレンス知覚ぼかしメトリックは [1] に記述されています。

[1]

Frederique Crete, Thierry Dolmiere, Patricia Ladret, and Marina Nicolas “The blur effect: perception and estimation with a new no-reference perceptual blur metric” Proc. SPIE 6492, Human Vision and Electronic Imaging XII, 64920I (2007) https://hal.archives-ouvertes.fr/hal-00232709 DOI:10.1117/12.702790

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy.ndimage as ndi

import plotly
import plotly.express as px
from skimage import color, data, measure

ぼかしが徐々に強くなる画像系列の生成

scikit-imageのデータレジストリから入手できる画像を読み込みましょう。ぼかしメトリックはシングルチャネル画像に適用されます。

image = data.astronaut()
image = color.rgb2gray(image)

この画像を、サイズが徐々に大きくなる一連の均一フィルターでぼかしてみましょう。

blurred_images = [ndi.uniform_filter(image, size=k) for k in range(2, 32, 2)]
img_stack = np.stack(blurred_images)

fig = px.imshow(
    img_stack,
    animation_frame=0,
    binary_string=True,
    labels={'animation_frame': 'blur strength ~'},
)
plotly.io.show(fig)

ぼかしメトリックのプロット

すべてのぼかし画像についてぼかしメトリックを計算してみましょう。ぼかしの強度が増すにつれて1に向かって増加することが予想されます。再ぼかしフィルターの3つの異なる値（3、11（デフォルト）、および30）について計算します。

B = pd.DataFrame(
    data=np.zeros((len(blurred_images), 3)),
    columns=['h_size = 3', 'h_size = 11', 'h_size = 30'],
)
for ind, im in enumerate(blurred_images):
    B.loc[ind, 'h_size = 3'] = measure.blur_effect(im, h_size=3)
    B.loc[ind, 'h_size = 11'] = measure.blur_effect(im, h_size=11)
    B.loc[ind, 'h_size = 30'] = measure.blur_effect(im, h_size=30)

B.plot().set(
    xlabel='blur strength (half the size of uniform filter)', ylabel='blur metric'
)

plt.show()

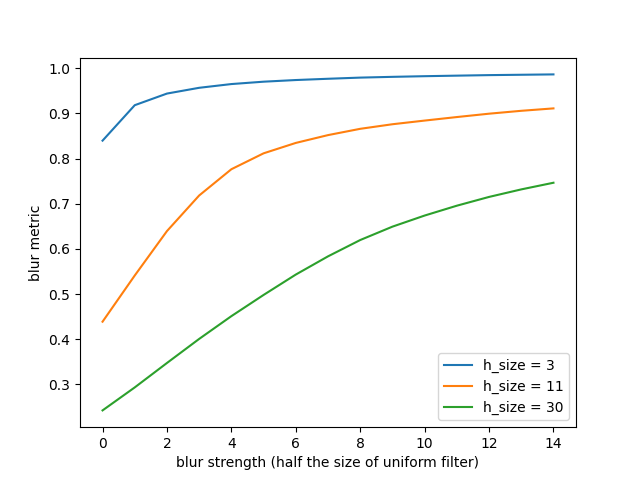
ぼかしが均一フィルターのサイズよりも強くなる（スケールに達する）とすぐに、メトリックは1に近づき、したがって、ぼかしの強度が増すにつれて漸近的に1になる傾向があることがわかります。11ピクセルの値は、人間の知覚と最もよく相関するぼかしメトリックを提供します。そのため、知覚ぼかしメトリック `measure.blur_effect` の実装ではデフォルト値になっています。