注記
完全なサンプルコードをダウンロードするにはこちらへ。またはBinder経由でブラウザでこの例を実行するには。
3D顕微鏡画像における異方性の推定#
このチュートリアルでは、3D画像の構造テンソルを計算します。3D画像処理の一般的な紹介については、3D画像(細胞)の探索を参照してください。ここで使用するデータは、共焦点蛍光顕微鏡によって得られた腎臓組織の画像からサンプリングされたものです(詳細については[1]のkidney-tissue-fluorescence.tifを参照)。
import matplotlib.pyplot as plt
import numpy as np
import plotly.express as px
import plotly.io
from skimage import data, feature
画像の読み込み#
この生物医学画像は、scikit-imageのデータレジストリから入手できます。
data = data.kidney()
3Dマルチチャネル画像の形状とサイズは正確にはどのくらいですか?
print(f'number of dimensions: {data.ndim}')
print(f'shape: {data.shape}')
print(f'dtype: {data.dtype}')
number of dimensions: 4
shape: (16, 512, 512, 3)
dtype: uint16
このチュートリアルの目的のために、2番目のカラーチャネルのみを考慮します。これにより、3Dシングルチャネル画像になります。値の範囲は?
range: (68, 4095)
3D画像の中央スライスを可視化してみましょう。
相対的なX-Y等方性を示す特定の領域を選択してみましょう。対照的に、勾配はZ方向にかなり異なり(そして、弱いです)。
sample = data[5:13, 380:410, 370:400, 1]
step = 3
cols = sample.shape[0] // step + 1
_, axes = plt.subplots(nrows=1, ncols=cols, figsize=(16, 8))
for it, (ax, image) in enumerate(zip(axes.flatten(), sample[::step])):
ax.imshow(image, cmap='gray', vmin=v_min, vmax=v_max)
ax.set_title(f'Plane = {5 + it * step}')
ax.set_xticks([])
ax.set_yticks([])
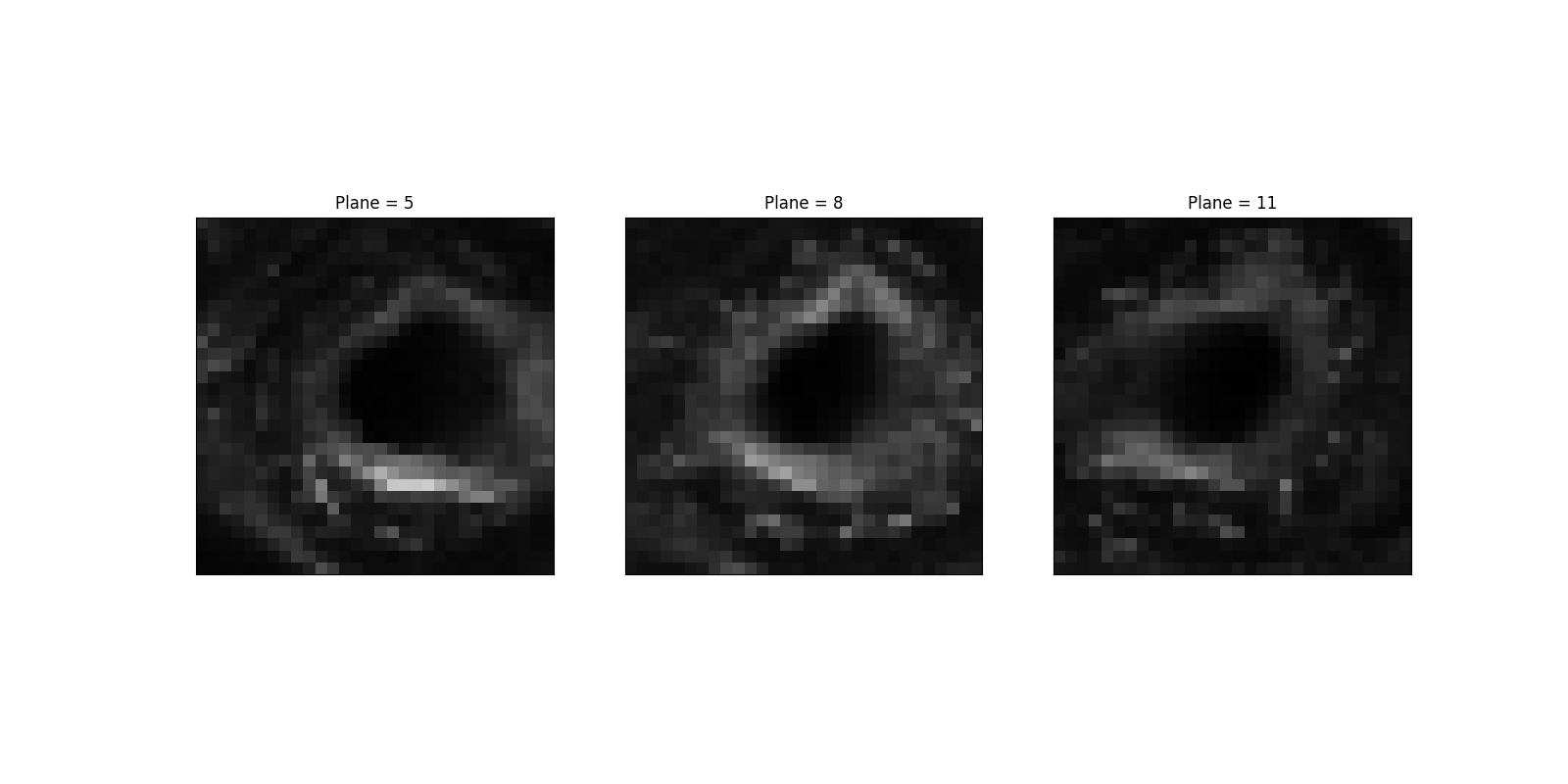
3Dでサンプルデータを表示するには、次のコードを実行します。
import plotly.graph_objects as go
(n_Z, n_Y, n_X) = sample.shape
Z, Y, X = np.mgrid[:n_Z, :n_Y, :n_X]
fig = go.Figure(
data=go.Volume(
x=X.flatten(),
y=Y.flatten(),
z=Z.flatten(),
value=sample.flatten(),
opacity=0.5,
slices_z=dict(show=True, locations=[4])
)
)
fig.show()
構造テンソルの計算#
サンプルデータの下部スライスを可視化し、大きな変化の典型的なサイズを決定しましょう。このサイズをウィンドウ関数の「幅」として使用します。
最も明るい領域(つまり、行〜22、列〜17)について、列(それぞれ行)全体で2〜3(それぞれ1〜2)ピクセルにわたる変化(したがって、強い勾配)が見られます。したがって、ウィンドウ関数に対してsigma = 1.5を選択できます。あるいは、軸ごとにsigmaを渡すこともできます(例:sigma = (1, 2, 3))。サイズは8(13 - 5)なので、最初の(Z、平面)軸に沿ってサイズ1は妥当です。X-Z平面またはY-Z平面のスライスを見ると、妥当であることがわかります。
次に、構造テンソルの固有値を計算できます。
(3, 8, 30, 30)
最大の固有値はどこにありますか?
coords = np.unravel_index(eigen.argmax(), eigen.shape)
assert coords[0] == 0 # by definition
coords
(np.int64(0), np.int64(1), np.int64(22), np.int64(16))
注記
読者は、この結果(座標(plane, row, column) = coords[1:])がsigmaの変更に対してどの程度堅牢であるかを確認できます。
最大の固有値が見つかったX-Y平面(つまり、Z = coords[1])における固有値の空間分布を見てみましょう。
