エントロピー

情報理論では、インフォメーションエントロピーはメッセージの可能な outcome の 2 を底とする対数です。

画像の場合、局所エントロピーは、通常構造要素によって定義される指定された近隣の領域に含まれる複雑さに関連しています。エントロピーフィルタは、局所的なグレースケール分布の微妙な変化を検出できます。

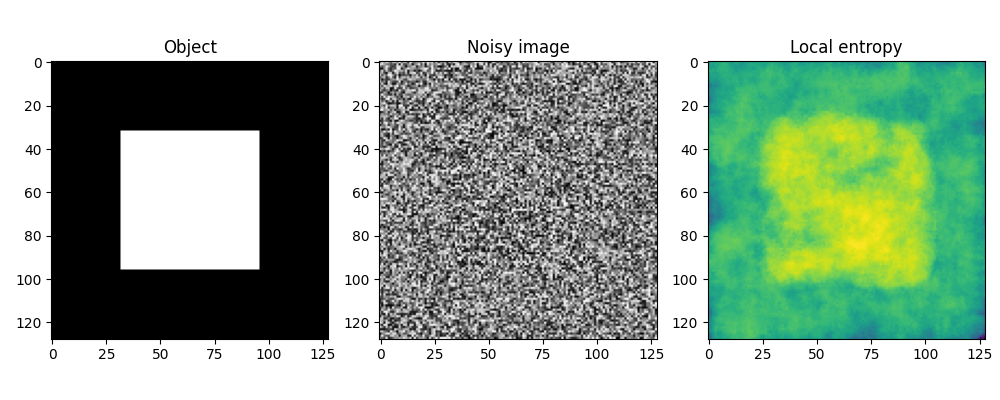
最初の例では、画像はわずかに異なる 2 つの分布を持つ 2 つのサーフェスで構成されています。画像の真ん中には [-15、+15] の範囲での一様な乱数分布があり、画像の境界には [-14、14] の範囲での一様な乱数分布があり、どちらの画像もグレースケール値 128 に中心があります。中央の正方形を検出するには、局所グレースケール分布を捉えるのに十分な大きさの円形構造要素を使用して、局所エントロピー尺度を計算します。2 つ目の例は、より小さな構造要素を使用してカメラ画像のテクスチャを検出する方法を示しています。

オブジェクト検出

import matplotlib.pyplot as plt
import numpy as np

from skimage import data
from skimage.util import img_as_ubyte
from skimage.filters.rank import entropy
from skimage.morphology import disk

rng = np.random.default_rng()

noise_mask = np.full((128, 128), 28, dtype=np.uint8)
noise_mask[32:-32, 32:-32] = 30

noise = (noise_mask * rng.random(noise_mask.shape) - 0.5 * noise_mask).astype(np.uint8)
img = noise + 128

entr_img = entropy(img, disk(10))

fig, (ax0, ax1, ax2) = plt.subplots(nrows=1, ncols=3, figsize=(10, 4))

img0 = ax0.imshow(noise_mask, cmap='gray')
ax0.set_title("Object")
ax1.imshow(img, cmap='gray')
ax1.set_title("Noisy image")
ax2.imshow(entr_img, cmap='viridis')
ax2.set_title("Local entropy")

fig.tight_layout()

テクスチャ検出

image = img_as_ubyte(data.camera())

fig, (ax0, ax1) = plt.subplots(ncols=2, figsize=(12, 4), sharex=True, sharey=True)

img0 = ax0.imshow(image, cmap=plt.cm.gray)
ax0.set_title("Image")
ax0.axis("off")
fig.colorbar(img0, ax=ax0)

img1 = ax1.imshow(entropy(image, disk(5)), cmap='gray')
ax1.set_title("Entropy")
ax1.axis("off")
fig.colorbar(img1, ax=ax1)

fig.tight_layout()

plt.show()