背景強度推定にローリングボールアルゴリズムを使用する

ローリングボールアルゴリズムは、不均一な露出の場合にグレースケール画像の背景強度を推定します。これは、生物医学画像処理で頻繁に使用され、1983年にスタンリー・R・スターンバーグによって最初に提案されました[1]。

このアルゴリズムはフィルターとして機能し、非常に直感的です。画像は、各ピクセルの代わりに互いに積み重ねられた単位サイズのブロックを持つ表面と見なします。ブロックの数、つまり表面の高さは、ピクセルの強度によって決定されます。目的の（ピクセル）位置で背景の強度を取得するには、目的の位置でボールを表面の下に沈めることを想像します。ボールがブロックで完全に覆われると、ボールの頂点がその位置での背景の強度を決定します。次に、このボールを表面の下で転がして、画像全体の背景値を取得できます。

Scikit-imageは、このローリングボールアルゴリズムの一般的なバージョンを実装しており、ボールだけでなく、任意の形状をカーネルとして使用でき、n次元ndimageで動作します。これにより、RGB画像を直接フィルタリングしたり、任意の（またはすべての）空間次元に沿って画像スタックをフィルタリングしたりできます。

[1]

Sternberg, Stanley R. “Biomedical image processing.” Computer 1 (1983): 22-34. DOI:10.1109/MC.1983.1654163

古典的なローリングボール

scikit-imageでは、ローリングボールアルゴリズムは、背景の強度が低い（黒）、一方、特徴の強度が高い（白）ことを前提としています。画像がこのようになっている場合は、次のようにフィルターを直接使用できます

import matplotlib.pyplot as plt
import numpy as np
import pywt

from skimage import data, restoration, util


def plot_result(image, background):
    fig, ax = plt.subplots(nrows=1, ncols=3)

    ax[0].imshow(image, cmap='gray')
    ax[0].set_title('Original image')
    ax[0].axis('off')

    ax[1].imshow(background, cmap='gray')
    ax[1].set_title('Background')
    ax[1].axis('off')

    ax[2].imshow(image - background, cmap='gray')
    ax[2].set_title('Result')
    ax[2].axis('off')

    fig.tight_layout()


image = data.coins()

background = restoration.rolling_ball(image)

plot_result(image, background)
plt.show()

白い背景

明るい背景に暗い特徴がある場合は、アルゴリズムに渡す前に画像を反転し、次に結果を反転する必要があります。これは、次の方法で実現できます

image = data.page()
image_inverted = util.invert(image)

background_inverted = restoration.rolling_ball(image_inverted, radius=45)
filtered_image_inverted = image_inverted - background_inverted
filtered_image = util.invert(filtered_image_inverted)
background = util.invert(background_inverted)

fig, ax = plt.subplots(nrows=1, ncols=3)

ax[0].imshow(image, cmap='gray')
ax[0].set_title('Original image')
ax[0].axis('off')

ax[1].imshow(background, cmap='gray')
ax[1].set_title('Background')
ax[1].axis('off')

ax[2].imshow(filtered_image, cmap='gray')
ax[2].set_title('Result')
ax[2].axis('off')

fig.tight_layout()

plt.show()

明るい背景を減算するときに整数アンダーフローに陥らないように注意してください。たとえば、このコードは正しく見えますが、アンダーフローが発生して不要なアーティファクトが発生する可能性があります。これは、視覚化の右上隅で確認できます。

image = data.page()
image_inverted = util.invert(image)

background_inverted = restoration.rolling_ball(image_inverted, radius=45)
background = util.invert(background_inverted)
underflow_image = image - background  # integer underflow occurs here

# correct subtraction
correct_image = util.invert(image_inverted - background_inverted)

fig, ax = plt.subplots(nrows=1, ncols=2)

ax[0].imshow(underflow_image, cmap='gray')
ax[0].set_title('Background Removal with Underflow')
ax[0].axis('off')

ax[1].imshow(correct_image, cmap='gray')
ax[1].set_title('Correct Background Removal')
ax[1].axis('off')

fig.tight_layout()

plt.show()

画像データ型

rolling_ballは、np.uint8以外のデータ型も処理できます。これらは同じように関数に渡すことができます。

image = data.coins()[:200, :200].astype(np.uint16)

background = restoration.rolling_ball(image, radius=70.5)
plot_result(image, background)
plt.show()

ただし、[0, 1]に正規化された浮動小数点画像を使用する場合は注意が必要です。この場合、ボールは画像の強度よりもはるかに大きくなり、予期しない結果につながる可能性があります。

image = util.img_as_float(data.coins()[:200, :200])

background = restoration.rolling_ball(image, radius=70.5)
plot_result(image, background)
plt.show()

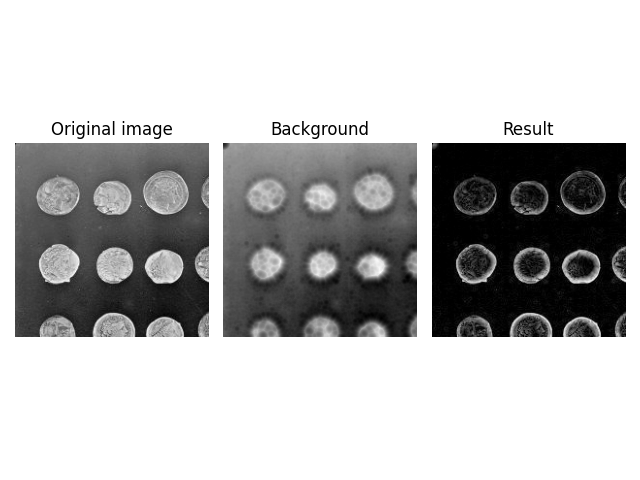
radius=70.5は画像の最大強度よりもはるかに大きいため、有効なカーネルサイズが大幅に縮小されます。つまり、ボールの小さなキャップ（約radius=10）のみが画像内で転がります。この奇妙な効果の再現は、下の高度な形状セクションで見つけることができます。

期待される結果を得るには、カーネルの強度を下げる必要があります。これは、kernel引数を使用してカーネルを手動で指定することで行われます。

注：半径は、楕円の半軸の長さに等しく、これは完全な軸の半分です。したがって、カーネル形状は2倍になります。

normalized_radius = 70.5 / 255
image = util.img_as_float(data.coins())
kernel = restoration.ellipsoid_kernel((70.5 * 2, 70.5 * 2), normalized_radius * 2)

background = restoration.rolling_ball(image, kernel=kernel)
plot_result(image, background)
plt.show()

高度な形状

デフォルトでは、rolling_ballは球形のカーネルを使用します（驚き）。場合によっては、上記の例のように、これは制限が大きすぎる可能性があります。強度の次元が空間次元と比較して異なるスケールを持っているため、または画像次元が異なる意味を持つ可能性があるためです。たとえば、画像スタック内のスタックカウンターである可能性があります。

これを考慮するために、rolling_ballには、使用するカーネルを指定できるkernel引数があります。カーネルは、画像と同じ次元を持っている必要があります（注：形状ではなく次元）。その作成を支援するために、2つのデフォルトのカーネルがskimageによって提供されています。ball_kernelは球形のカーネルを指定し、デフォルトのカーネルとして使用されます。ellipsoid_kernelは楕円形のカーネルを指定します。

image = data.coins()
kernel = restoration.ellipsoid_kernel((70.5 * 2, 70.5 * 2), 70.5 * 2)

background = restoration.rolling_ball(image, kernel=kernel)
plot_result(image, background)
plt.show()

ellipsoid_kernelを使用して、以前の予期しない結果を再現し、有効な（空間）フィルターサイズが縮小されたことを確認することもできます。

image = data.coins()

kernel = restoration.ellipsoid_kernel((10 * 2, 10 * 2), 255 * 2)

background = restoration.rolling_ball(image, kernel=kernel)
plot_result(image, background)
plt.show()

高次元

rolling_ball のもう一つの特徴は、共焦点顕微鏡で取得した画像の z スタックなど、より高次元の画像に直接適用できることです。カーネルの次元数は画像の次元数と一致する必要があるため、カーネル形状は 3 次元になります。

image = data.cells3d()[:, 1, ...]
background = restoration.rolling_ball(
    image, kernel=restoration.ellipsoid_kernel((1, 21, 21), 0.1)
)

plot_result(image[30, ...], background[30, ...])
plt.show()

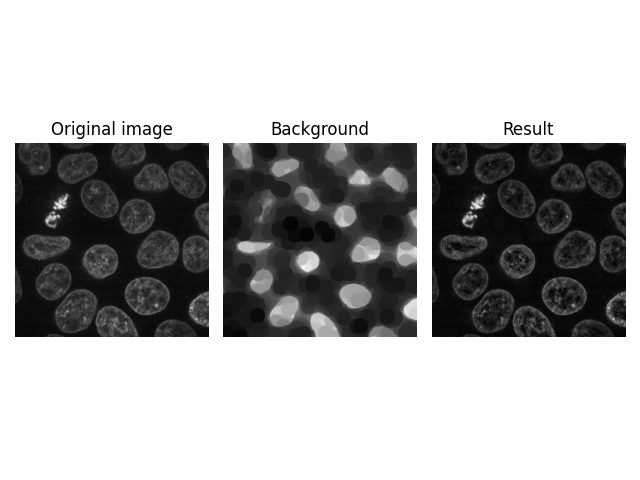
カーネルサイズが 1 の場合、この軸に沿ったフィルタリングは行われません。言い換えれば、上記のフィルターはスタック内の各画像に個別に適用されます。

ただし、1 以外の値を指定することで、3 次元すべてに同時にフィルタリングすることもできます。

image = data.cells3d()[:, 1, ...]
background = restoration.rolling_ball(
    image, kernel=restoration.ellipsoid_kernel((5, 21, 21), 0.1)
)

plot_result(image[30, ...], background[30, ...])
plt.show()

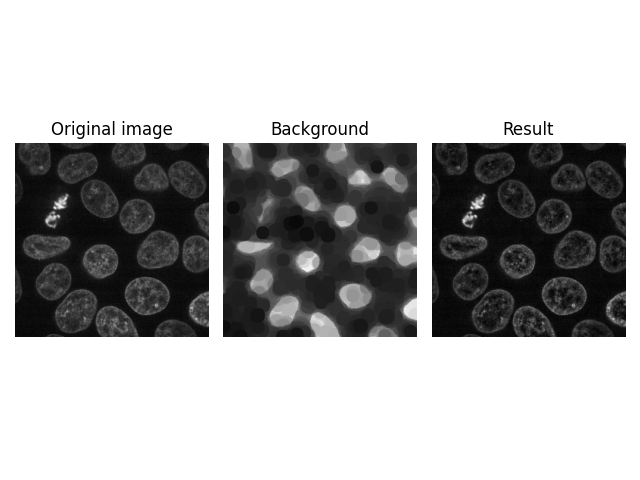
別の可能性として、平面軸 (z スタック軸) に沿って個々のピクセルをフィルタリングすることもできます。

image = data.cells3d()[:, 1, ...]
background = restoration.rolling_ball(
    image, kernel=restoration.ellipsoid_kernel((100, 1, 1), 0.1)
)

plot_result(image[30, ...], background[30, ...])
plt.show()

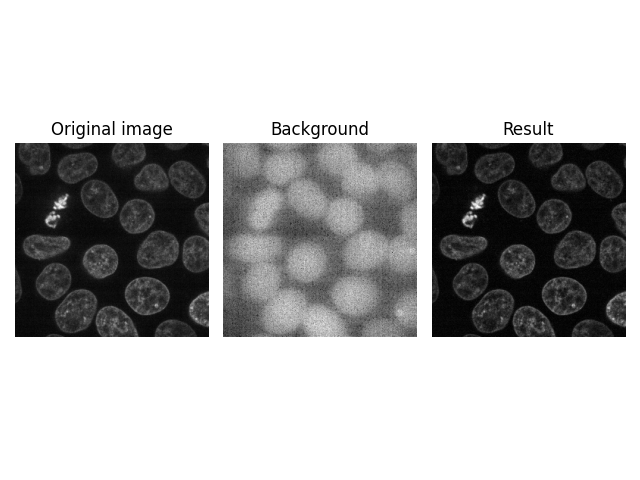
1D信号フィルタリング

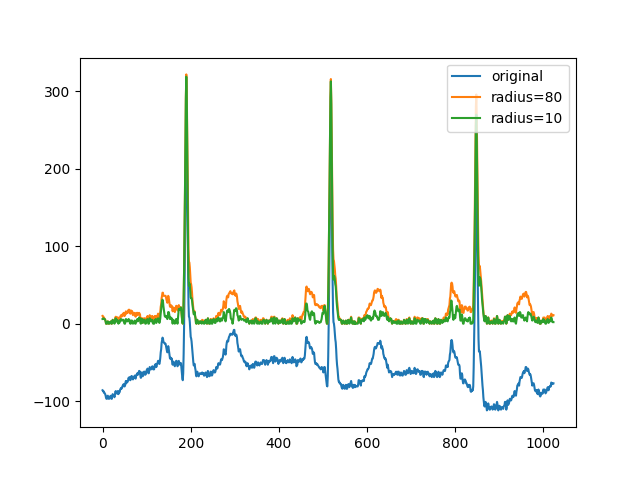
rolling_ball の n 次元機能の別の例として、1D データの実装を示します。ここでは、ECG 波形の背景信号を除去して、顕著なピーク (ローカルベースラインよりも高い値) を検出することに関心があります。より滑らかなピークは、半径の値を小さくすることで除去できます。

x = pywt.data.ecg()
background = restoration.rolling_ball(x, radius=80)
background2 = restoration.rolling_ball(x, radius=10)
plt.figure()
plt.plot(x, label='original')
plt.plot(x - background, label='radius=80')
plt.plot(x - background2, label='radius=10')
plt.legend()
plt.show()