コロケーションメトリクス

この例では、2 つの異なる画像チャネルのコロケーションを評価するためのさまざまなメトリクスの使用方法を示します。

コロケーションは 2 つの異なる概念に分割できます。1. 共起: 特定の領域に物質のどの割合が局所化されていますか? 2. 相関: 2 つの物質間の強度関係はどうなっていますか?

共起: 細胞内局在

タンパク質の細胞内局在を決定しようとしているとします。標的に比べて、核内に局在する割合がより高くなりますか、細胞質内に局在する割合がより高くなりますか?

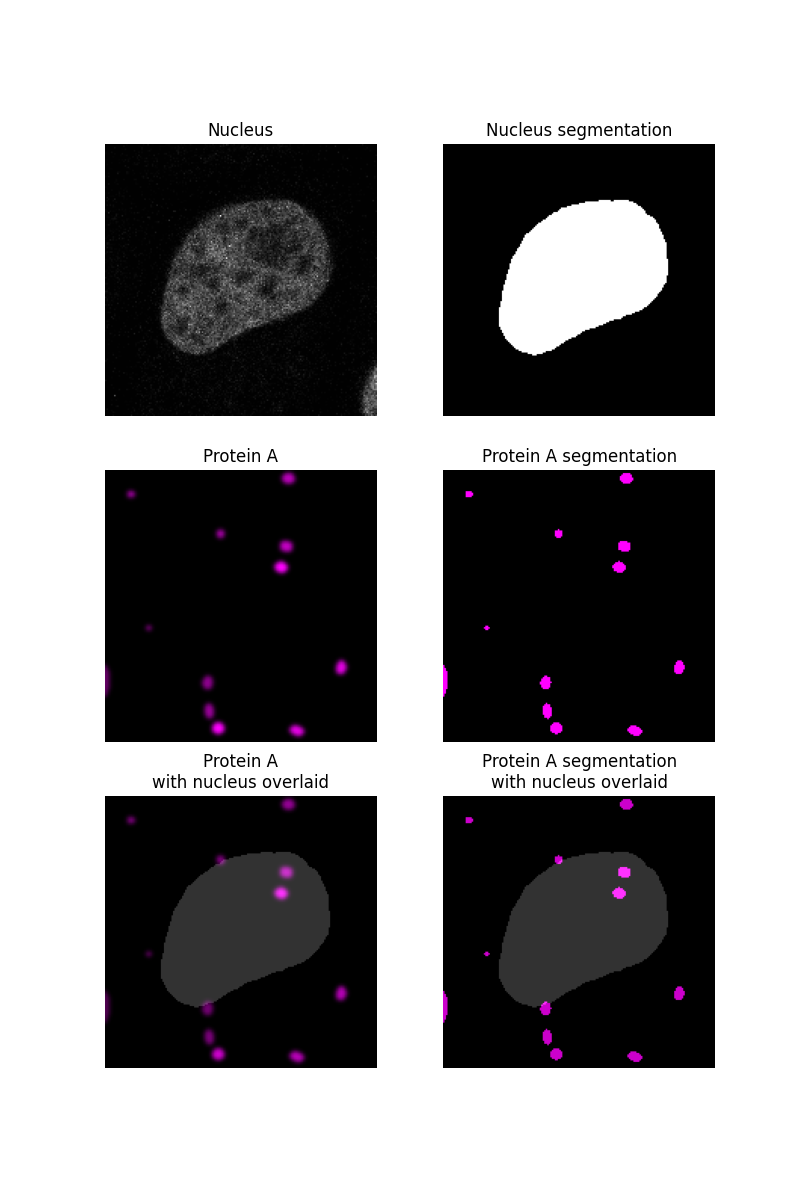
別の例で説明したように、サンプル画像の核をセグメント化することから始め、核内にないものはすべて細胞質内にあると仮定します。タンパク質「タンパク質 A」はブロブとしてシミュレートされ、セグメント化されます。

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.colors import LinearSegmentedColormap
from scipy import ndimage as ndi
from skimage import data, filters, measure, segmentation

rng = np.random.default_rng()

# segment nucleus
nucleus = data.protein_transport()[0, 0, :, :180]
smooth = filters.gaussian(nucleus, sigma=1.5)
thresh = smooth > filters.threshold_otsu(smooth)
fill = ndi.binary_fill_holes(thresh)
nucleus_seg = segmentation.clear_border(fill)

# protein blobs of varying intensity
proteinA = np.zeros_like(nucleus, dtype="float64")
proteinA_seg = np.zeros_like(nucleus, dtype="float64")

for blob_seed in range(10):
    blobs = data.binary_blobs(
        180, blob_size_fraction=0.5, volume_fraction=(50 / (180**2)), rng=blob_seed
    )
    blobs_image = filters.gaussian(blobs, sigma=1.5) * rng.integers(50, 256)
    proteinA += blobs_image
    proteinA_seg += blobs

# plot data
fig, ax = plt.subplots(3, 2, figsize=(8, 12), sharey=True)
ax[0, 0].imshow(nucleus, cmap=plt.cm.gray)
ax[0, 0].set_title('Nucleus')

ax[0, 1].imshow(nucleus_seg, cmap=plt.cm.gray)
ax[0, 1].set_title('Nucleus segmentation')

black_magenta = LinearSegmentedColormap.from_list("", ["black", "magenta"])
ax[1, 0].imshow(proteinA, cmap=black_magenta)
ax[1, 0].set_title('Protein A')

ax[1, 1].imshow(proteinA_seg, cmap=black_magenta)
ax[1, 1].set_title('Protein A segmentation')

ax[2, 0].imshow(proteinA, cmap=black_magenta)
ax[2, 0].imshow(nucleus_seg, cmap=plt.cm.gray, alpha=0.2)
ax[2, 0].set_title('Protein A\nwith nucleus overlaid')

ax[2, 1].imshow(proteinA_seg, cmap=black_magenta)
ax[2, 1].imshow(nucleus_seg, cmap=plt.cm.gray, alpha=0.2)
ax[2, 1].set_title('Protein A segmentation\nwith nucleus overlaid')

for a in ax.ravel():
    a.set_axis_off()

交差係数

核と目的タンパク質の両方のセグメンテーションの後、タンパク質 A セグメンテーションが核セグメンテーションと重なる割合を決定できます。

measure.intersection_coeff(proteinA_seg, nucleus_seg)

0.22

マンダーズ共局在係数 (MCC)

オーバーラップ係数では、タンパク質セグメンテーションの領域がタンパク質の濃度に相当すると想定され、領域が大きいほどタンパク質が多いことを示します。画像の解像度は通常、個々のタンパク質を見分けるには小さすぎるため、1 つのピクセル内で固まることがあり、そのピクセルの強度が明るくなります。そのため、タンパク質濃度をより正確に捉えるために、タンパク質チャネルの強度のどの程度の割合が核内にあるかを決定できます。この指標はマンダーズ共局在係数として知られています。

この画像では、核内に多くのタンパク質 A スポットがありますが、核外のスポットに比べて見劣りするので、MCC はオーバーラップ係数よりもはるかに低くなります。

measure.manders_coloc_coeff(proteinA, nucleus_seg)

np.float64(0.2566709686373243)

共存指標を選択した後、同じプロセスを制御画像に適用できます。制御画像がない場合は、コスト法を使用して、元の画像の MCC 値とランダムにシャッフルした画像の値を比較できます。この方法に関する情報は、[1]で提供されています。

[1]

J. S. アーロン、A. B. テイラー、T.-L. チュウ、画像共局在 - 共存対相関。J Cell Sci、2018 年 2 月 1 日、131 (3): jcs211847。doi: https://doi.org/10.1242/jcs.211847

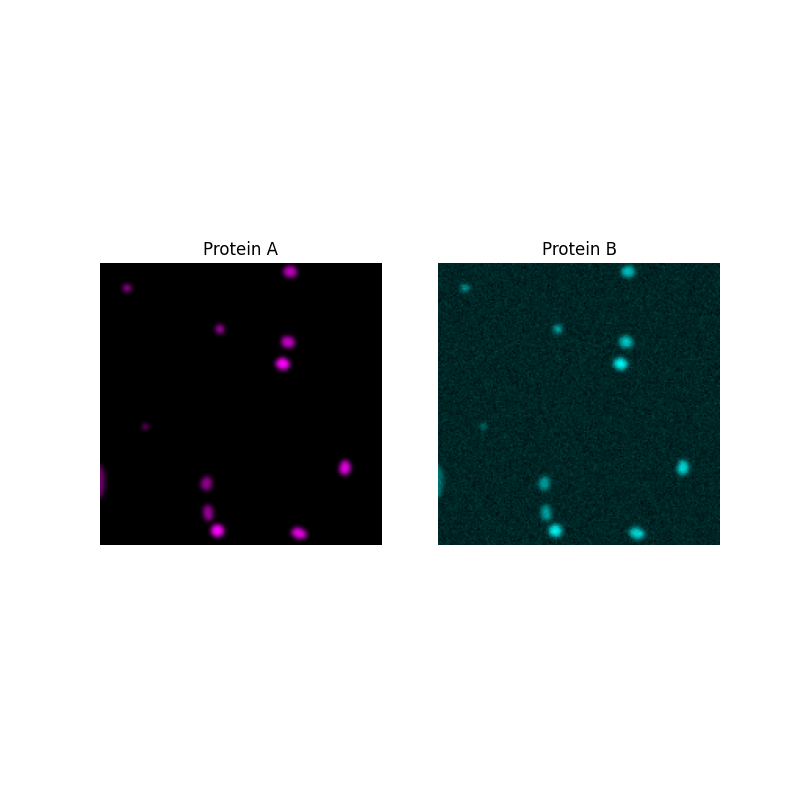
相関: 2 つのタンパク質の関連性

それでは、2 つのタンパク質の関連性がどれほど近いのかを知りたいとします。

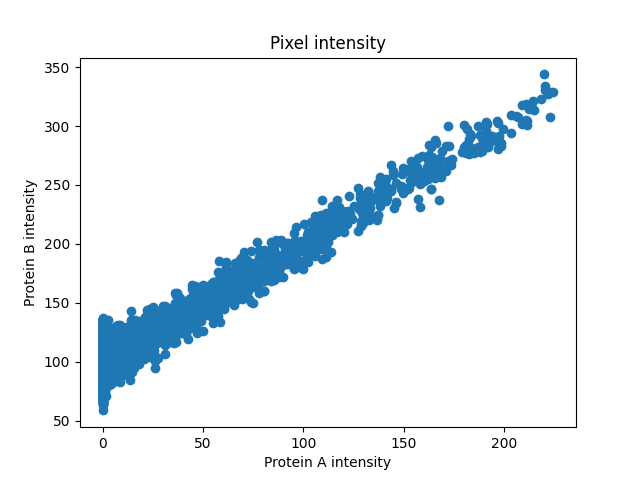
まず、タンパク質 B を生成し、各ピクセルで 2 つのタンパク質の強度をプロットして、それらの間の関係を確認します。

# generating protein B data that is correlated to protein A for demo
proteinB = proteinA + rng.normal(loc=100, scale=10, size=proteinA.shape)

# plot images
fig, ax = plt.subplots(1, 2, figsize=(8, 8), sharey=True)

ax[0].imshow(proteinA, cmap=black_magenta)
ax[0].set_title('Protein A')

black_cyan = LinearSegmentedColormap.from_list("", ["black", "cyan"])
ax[1].imshow(proteinB, cmap=black_cyan)
ax[1].set_title('Protein B')

for a in ax.ravel():
    a.set_axis_off()

# plot pixel intensity scatter
fig, ax = plt.subplots()
ax.scatter(proteinA, proteinB)
ax.set_title('Pixel intensity')
ax.set_xlabel('Protein A intensity')
ax.set_ylabel('Protein B intensity')

• 
• 

Text(38.347222222222214, 0.5, 'Protein B intensity')

強度は線形相関があるように見えるため、ピアソンの相関係数は関連性がどれほど強いかの良い測定値になります。

pcc, pval = measure.pearson_corr_coeff(proteinA, proteinB)
print(f"PCC: {pcc:0.3g}, p-val: {pval:0.3g}")

PCC: 0.857, p-val: 0

場合によっては、強度が相関しているものの線形ではないことがあります。スピアマンなどのランクベースの相関係数は、その場合、非線形関係のより正確な測定を提供する可能性があります。

plt.show()