skimage.measure#
画像プロパティ(例えば、領域プロパティ、輪郭)の測定。
指定された許容値でポリゴンチェーンを近似します。 |
|
ローカルブロックに関数 |
|
画像内のぼかしの強さを示す指標を計算します(ぼかしがない場合は0、最大のぼかしの場合は1)。 |
|
画像の(重み付き)重心を返します。 |
|
バイナリ画像内のオイラー標数を計算します。 |
|
指定されたレベル値に対する2D配列内の等値輪郭を検出します。 |
|
指定されたグリッド上の点がポリゴン内にあるかどうかをテストします。 |
|
入力画像の慣性テンソルを計算します。 |
|
画像の慣性テンソルの固有値を計算します。 |
|
チャンネルのセグメント化されたバイナリマスクが、2番目のチャンネルのセグメント化されたバイナリマスクと重複する割合。 |
|
整数配列の連結領域にラベルを付けます。 |
|
2つのチャンネル間のマンダースのコロケーション係数。 |
|
マンダースのオーバーラップ係数 |
|
3Dボリュームデータ内の表面を検出するためのマーチングキューブアルゴリズム。 |
|
頂点と三角形の面が与えられた場合、表面積を計算します。 |
|
特定の次数までのすべての生の画像モーメントを計算します。 |
|
特定の次数までのすべての中央画像モーメントを計算します。 |
|
特定の次数までのすべての生の画像モーメントを計算します。 |
|
特定の次数までのすべての中央画像モーメントを計算します。 |
|
Huの画像モーメントセット(2Dのみ)を計算します。 |
|
特定の次数までのすべての正規化された中央画像モーメントを計算します。 |
|
チャンネルのピクセル強度間のピアソンの相関係数を計算します。 |
|
バイナリ画像内のすべてのオブジェクトの合計周囲長を計算します。 |
|
バイナリ画像内のすべてのオブジェクトの合計クロフトン周囲長を計算します。 |
|
点がポリゴン内にあるかどうかをテストします。 |
|
スキャンラインに沿って測定された画像の強度プロファイルを返します。 |
|
RANSAC(ランダムサンプルコンセンサス)アルゴリズムを使用して、データにモデルを適合させます。 |
|
ラベル付き画像領域のプロパティを測定します。 |
|
画像プロパティを計算し、pandas互換のテーブルとして返します。 |
|
画像のシャノンエントロピーを計算します。 |
|
Bスプラインを使用したポリゴン曲線の細分化。 |
|
2D円の総最小二乗推定量。 |
|
2D楕円の総最小二乗推定量。 |
|
N次元線の総最小二乗推定量。 |
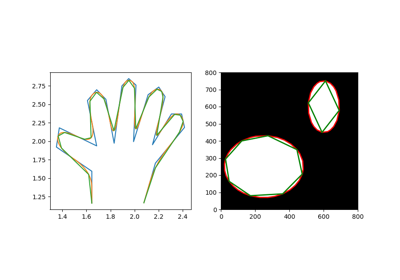
- skimage.measure.approximate_polygon(coords, tolerance)[ソース]#
指定された許容値でポリゴンチェーンを近似します。
ダグラス-ポイカーアルゴリズムに基づいています。
近似されたポリゴンは、常に元のポリゴンの凸包内にあることに注意してください。
- パラメーター:
- coords(K, 2) 配列
座標配列。
- tolerancefloat
ポリゴンの元の点から近似されたポリゴンチェーンまでの最大距離。許容値が0の場合、元の座標配列が返されます。
- 戻り値:
- coords(L, 2) 配列
近似されたポリゴンチェーン。ここで、L <= Kです。
参考文献
- skimage.measure.block_reduce(image, block_size=2, func=<function sum>, cval=0, func_kwargs=None)[ソース]#
ローカルブロックに関数
funcを適用して、画像をダウンサンプリングします。この関数は、例えば最大値プーリングや平均値プーリングに役立ちます。
- パラメーター:
- image(M[, …]) ndarray
N次元入力画像。
- block_size配列状またはint
各軸に沿ったダウンサンプリング整数係数を含む配列。デフォルトのblock_sizeは2です。
- funccallable
各ローカルブロックの戻り値を計算するために使用される関数オブジェクト。この関数は
axisパラメーターを実装する必要があります。主な関数は、numpy.sum、numpy.min、numpy.max、numpy.mean、およびnumpy.medianです。func_kwargsも参照してください。- cvalfloat
画像がブロックサイズで完全に割り切れない場合の定数パディング値。
- func_kwargsdict
funcに渡されるキーワード引数。特に、np.meanにdtype引数を渡すのに役立ちます。例えば、func_kwargs={'dtype': np.float16})のように入力の辞書をとります。
- 戻り値:
- imagendarray
入力画像と同じ次元数を持つダウンサンプリングされた画像。
例
>>> from skimage.measure import block_reduce >>> image = np.arange(3*3*4).reshape(3, 3, 4) >>> image array([[[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]], [[12, 13, 14, 15], [16, 17, 18, 19], [20, 21, 22, 23]], [[24, 25, 26, 27], [28, 29, 30, 31], [32, 33, 34, 35]]]) >>> block_reduce(image, block_size=(3, 3, 1), func=np.mean) array([[[16., 17., 18., 19.]]]) >>> image_max1 = block_reduce(image, block_size=(1, 3, 4), func=np.max) >>> image_max1 array([[[11]], [[23]], [[35]]]) >>> image_max2 = block_reduce(image, block_size=(3, 1, 4), func=np.max) >>> image_max2 array([[[27], [31], [35]]])
- skimage.measure.blur_effect(image, h_size=11, channel_axis=None, reduce_func=<function max>)[ソース]#
画像内のぼかしの強さを示す指標を計算します(ぼかしがない場合は0、最大のぼかしの場合は1)。
- パラメーター:
- imagendarray
RGBまたはグレースケールnD画像。入力画像は、ぼかしメトリックを計算する前にグレースケールに変換されます。
- h_sizeint、オプション
再ぼかしフィルターのサイズ。
- channel_axisintまたはNone、オプション
Noneの場合、画像はグレースケール(単一チャンネル)であると想定されます。それ以外の場合、このパラメーターは配列のどの軸がカラーチャンネルに対応するかを示します。
- reduce_funccallable、オプション
すべての軸に沿ったぼかしメトリックの集計を計算するために使用される関数。Noneに設定した場合、リスト全体が返され、i番目の要素はi番目の軸に沿ったぼかしメトリックになります。
- 戻り値:
- blurfloat (0〜1) またはfloatのリスト
ぼかしメトリック:デフォルトでは、すべての軸に沿ったぼかしメトリックの最大値。
注記
h_sizeは、画像間で結果を比較するために同じ値を保持する必要があります。ほとんどの場合、デフォルトのサイズ(11)で十分です。これは、メトリックが平均11x11フィルターまでのぼかしを明確に識別できることを意味します。ぼかしが大きい場合でも、メトリックは良好な結果をもたらしますが、その値は漸近線に向かう傾向があります。参考文献
[1]Frederique Crete、Thierry Dolmiere、Patricia Ladret、およびMarina Nicolas「The blur effect: perception and estimation with a new no-reference perceptual blur metric」Proc. SPIE 6492, Human Vision and Electronic Imaging XII, 64920I (2007) https://hal.archives-ouvertes.fr/hal-00232709 DOI:10.1117/12.702790
- skimage.measure.centroid(image, *, spacing=None)[ソース]#
画像の(重み付き)重心を返します。
- パラメーター:
- image配列
入力画像。
- spacing: float のタプル、形状 (ndim,)
画像の各軸に沿ったピクセル間隔。
- 戻り値:
- centerfloat のタプル、長さ
image.ndim image内の (ゼロでない) ピクセルの重心。
- centerfloat のタプル、長さ
例
>>> image = np.zeros((20, 20), dtype=np.float64) >>> image[13:17, 13:17] = 0.5 >>> image[10:12, 10:12] = 1 >>> centroid(image) array([13.16666667, 13.16666667])
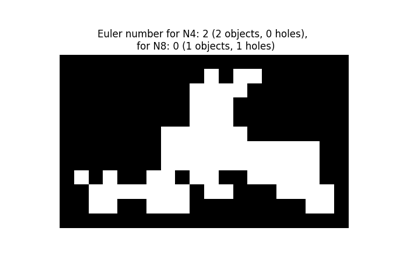
- skimage.measure.euler_number(image, connectivity=None)[ソース]#
バイナリ画像内のオイラー標数を計算します。
2D オブジェクトの場合、オイラー数はオブジェクトの数から穴の数を引いたものです。3D オブジェクトの場合、オイラー数はオブジェクトの数に穴の数を足し、そこからトンネルまたはループの数を引いたものとして得られます。
- パラメーター:
- image: (M, N[, P]) ndarray
入力画像。画像がバイナリでない場合、ゼロより大きいすべての値がオブジェクトと見なされます。
- connectivityint, optional
ピクセル/ボクセルを隣接とみなすために考慮する直交ホップの最大数。受け入れられる値は 1 から input.ndim の範囲です。
Noneの場合、input.ndimの完全な接続性が使用されます。2D 画像の場合、4 または 8 近傍が定義されます (それぞれ接続性 1 および 2)。3D 画像の場合、6 または 26 近傍が定義されます (それぞれ接続性 1 および 3)。接続性 2 は定義されていません。
- 戻り値:
- euler_numberint
画像内のすべてのオブジェクトの集合のオイラー標数。
注記
オイラー標数は、入力画像内のすべてのオブジェクトの集合のトポロジーを記述する整数です。オブジェクトが 4 連結の場合、背景は 8 連結になり、逆にそのようになります。
オイラー標数の計算は、離散空間における積分幾何学的公式に基づいています。実際には、近傍構成が構築され、各構成に LUT が適用されます。使用される係数は、Ohser らの係数です。
複数の接続性に対してオイラー標数を計算すると便利な場合があります。異なる接続性に対する結果の相対的な差が大きい場合、(オブジェクトと穴のサイズに対する) 画像の解像度が低すぎることを示唆しています。
参考文献
[1]S. Rivollier. Analyse d’image geometrique et morphometrique par diagrammes de forme et voisinages adaptatifs generaux. PhD thesis, 2010. Ecole Nationale Superieure des Mines de Saint-Etienne. https://tel.archives-ouvertes.fr/tel-00560838
[2]Ohser J., Nagel W., Schladitz K. (2002) The Euler Number of Discretized Sets - On the Choice of Adjacency in Homogeneous Lattices. In: Mecke K., Stoyan D. (eds) Morphology of Condensed Matter. Lecture Notes in Physics, vol 600. Springer, Berlin, Heidelberg.
例
>>> import numpy as np >>> SAMPLE = np.zeros((100,100,100)); >>> SAMPLE[40:60, 40:60, 40:60]=1 >>> euler_number(SAMPLE) 1... >>> SAMPLE[45:55,45:55,45:55] = 0; >>> euler_number(SAMPLE) 2... >>> SAMPLE = np.array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0], ... [0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0], ... [1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0], ... [0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1], ... [0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1]]) >>> euler_number(SAMPLE) # doctest: 0 >>> euler_number(SAMPLE, connectivity=1) # doctest: 2
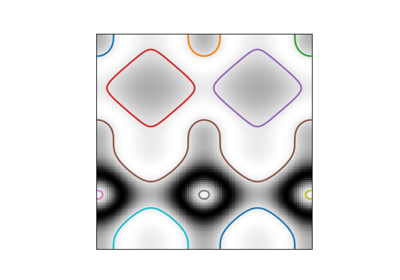
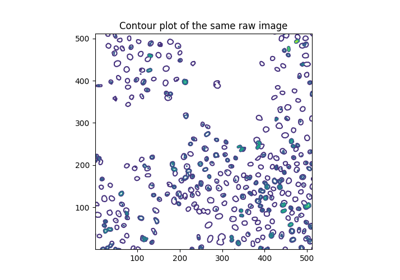
- skimage.measure.find_contours(image, level=None, fully_connected='low', positive_orientation='low', *, mask=None)[ソース]#
指定されたレベル値に対する2D配列内の等値輪郭を検出します。
「マーチングスクエア」法を使用して、特定のレベル値の入力 2D 配列の等値輪郭を計算します。配列値は線形に補間され、出力輪郭の精度が向上します。
- パラメーター:
- image(M, N) double の ndarray
輪郭を見つける入力画像。
- levelfloat, optional
配列内の輪郭を見つける値。デフォルトでは、レベルは (max(image) + min(image)) / 2 に設定されます。
バージョン 0.18 で変更: このパラメーターはオプションになりました。
- fully_connectedstr, {‘low’, ‘high’}
指定されたレベル値よりも下の配列要素を完全に接続されたと見なすか (したがって、値よりも上の要素は面接続のみになります)、またはその逆かを示します。(詳細については、下記の注記を参照してください。)
- positive_orientationstr, {‘low’, ‘high’}
出力輪郭が、低値または高値の要素の島の周りに正の向きの多角形を生成するかどうかを示します。 ‘low’ の場合、輪郭は等値より下の要素の周りを反時計回りに進みます。あるいは、これは低値の要素が常に輪郭の左側にあることを意味します。(詳細については下記を参照してください。)
- mask(M, N) bool の ndarray または None
輪郭を描画したい場所で True のブールマスク。 NaN 値は常に考慮される領域から除外されることに注意してください (
maskはarrayがNaNである場所では常にFalseに設定されます)。
- 戻り値:
- contours(K, 2) ndarray のリスト
各輪郭は、輪郭に沿った
(行、 列)座標の ndarray です。
注記
マーチングスクエアアルゴリズムは、マーチングキューブアルゴリズムの特殊なケースです [1]。簡単な説明はこちらにあります
https://users.polytech.unice.fr/~lingrand/MarchingCubes/algo.html
マーチングスクエアアルゴリズムには、あいまいなケースが 1 つあります。与えられた
2 x 2要素の正方形に、対角線で隣接する 2 つの高値要素と 2 つの低値要素がある場合です。(ここで、高値および低値は、求められる輪郭値に関してです。)この場合、高値要素は、低値要素を分離する薄い地峡を介して「接続」されるか、またはその逆のいずれかになります。要素が対角線で接続されている場合、それらは「完全に接続」されていると見なされます (「面+頂点接続」または「8 接続」とも呼ばれます)。高値または低値の要素のみが完全に接続でき、他のセットは「面接続」または「4 接続」と見なされます。デフォルトでは、低値の要素は完全に接続されていると見なされます。これは ‘fully_connected’ パラメーターで変更できます。出力輪郭が閉じられていることは保証されません。配列の端またはマスクされた領域 (マスクが False の場所または配列が NaN の場所) と交差する輪郭は開いたままになります。他のすべての輪郭は閉じられます。(輪郭の閉じ具合は、開始点と終了点が同じかどうかを確認することでテストできます。)
輪郭は方向付けられています。デフォルトでは、輪郭値よりも低い配列値は輪郭の左側にあり、輪郭値よりも高い値は右側にあります。これは、輪郭が低値ピクセルの島の周りを反時計回り (つまり「正の向き」) に進むことを意味します。この動作は、’positive_orientation’ パラメーターで変更できます。
出力リストの輪郭の順序は、輪郭内の最小の
x,y(辞書順) 座標の位置によって決定されます。これは入力配列が走査される方法の副作用ですが、依存することができます。警告
配列の座標/値は、配列要素の中心を参照すると想定されています。簡単な入力例を見てみましょう:
[0, 1]。この配列の 0.5 の補間された位置は、0 要素 (x=0) と 1 要素 (x=1) の中間であり、したがってx=0.5になります。これは、妥当な輪郭を見つけるには、予想される「明るい」値と「暗い」値の中間で見つけるのが最善であることを意味します。特に、二値化された配列が与えられた場合、配列の低値または高値で輪郭を見つけることを選択しないでください。これは、特に単一の配列要素幅の構造の周りで、縮退した輪郭になることがよくあります。代わりに、上記のように中間値を選択してください。
参考文献
[1]Lorensen, William and Harvey E. Cline. Marching Cubes: A High Resolution 3D Surface Construction Algorithm. Computer Graphics (SIGGRAPH 87 Proceedings) 21(4) July 1987, p. 163-170). DOI:10.1145/37401.37422
例
>>> a = np.zeros((3, 3)) >>> a[0, 0] = 1 >>> a array([[1., 0., 0.], [0., 0., 0.], [0., 0., 0.]]) >>> find_contours(a, 0.5) [array([[0. , 0.5], [0.5, 0. ]])]
- skimage.measure.grid_points_in_poly(shape, verts, binarize=True)[ソース]#
指定されたグリッド上の点がポリゴン内にあるかどうかをテストします。
グリッド上の各
(r, c)座標 (つまり(0, 0)、(0, 1)など) について、その点が多角形の内側にあるかどうかをテストします。binarizeフラグを使用して、出力タイプを制御できます。詳細については、そのドキュメントを参照してください。- パラメーター:
- shapeタプル (M, N)
グリッドの形状。
- verts(V, 2) 配列
多角形の V 個の頂点を、時計回りまたは反時計回りのいずれかでソートして指定します。最初の点は重複しても構いません (必須ではありません)。
- binarize: bool
Trueの場合、関数の出力はブールマスクです。それ以外の場合は、ラベル付き配列です。ラベルは、O - 外側、1 - 内側、2 - 頂点、3 - エッジです。
- 戻り値:
- mask(M, N) ndarray
binarizeが True の場合、出力はブールマスクです。True は、対応するピクセルが多角形の内側にあることを意味します。binarizeが False の場合、出力はラベル付き配列で、ピクセルのラベルは 0 から 3 の間です。値の意味は、O - 外側、1 - 内側、2 - 頂点、3 - エッジです。
- skimage.measure.inertia_tensor(image, mu=None, *, spacing=None)[ソース]#
入力画像の慣性テンソルを計算します。
- パラメーター:
- image配列
入力画像。
- muarray, optional
imageの事前計算された中心モーメント。慣性テンソルの計算には、画像の中心モーメントが必要です。アプリケーションで中心モーメントと慣性テンソルの両方が必要な場合(たとえば、skimage.measure.regionprops)、それらを事前に計算して慣性テンソルの呼び出しに渡す方が効率的です。- spacing: float のタプル、形状 (ndim,)
画像の各軸に沿ったピクセル間隔。
- 戻り値:
- Tarray, shape
(image.ndim, image.ndim) 入力画像の慣性テンソル。\(T_{i, j}\) は、軸 \(i\) と \(j\) に沿った画像強度の共分散を含んでいます。
- Tarray, shape
参考文献
[2]Bernd Jähne. Spatio-Temporal Image Processing: Theory and Scientific Applications. (Chapter 8: Tensor Methods) Springer, 1993.
- skimage.measure.inertia_tensor_eigvals(image, mu=None, T=None, *, spacing=None)[ソース]#
画像の慣性テンソルの固有値を計算します。
慣性テンソルは、画像軸に沿った画像強度の共分散を測定します。(
inertia_tensorを参照)。したがって、テンソルの固有値の相対的な大きさは、画像内の(明るい)オブジェクトの伸長の尺度となります。- パラメーター:
- image配列
入力画像。
- muarray, optional
imageの事前計算された中心モーメント。- Tarray, shape
(image.ndim, image.ndim) 事前計算された慣性テンソル。
Tが与えられた場合、muとimageは無視されます。- spacing: float のタプル、形状 (ndim,)
画像の各軸に沿ったピクセル間隔。
- 戻り値:
- eigvalsfloat のリスト、長さ
image.ndim imageの慣性テンソルの固有値。降順に並んでいます。
- eigvalsfloat のリスト、長さ
注記
固有値を計算するには、入力画像の慣性テンソルが必要です。これは、中心モーメント (
mu) が提供されている場合、または代替として、慣性テンソル (T) を直接提供できる場合に大幅に高速化されます。
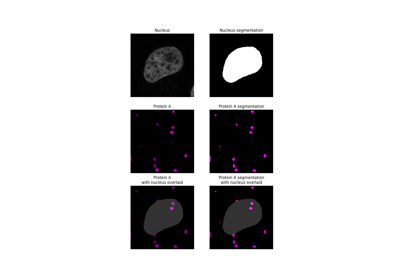
- skimage.measure.intersection_coeff(image0_mask, image1_mask, mask=None)[ソース]#
あるチャネルのセグメント化されたバイナリマスクが、別のチャネルのセグメント化されたバイナリマスクとオーバーラップする割合。
- パラメーター:
- image0_mask(M, N) dtype bool の ndarray
チャネル A の画像マスク。
- image1_mask(M, N) dtype bool の ndarray
チャネル B の画像マスク。
image0_maskと同じ次元でなければなりません。- mask(M, N) dtype bool の ndarray, optional
この関心領域マスク内の
image0_maskおよびimage1_maskのピクセルのみが計算に含まれます。image0_maskと同じ次元でなければなりません。
- 戻り値:
- 交差係数, float
image0_maskがimage1_maskとオーバーラップする割合。
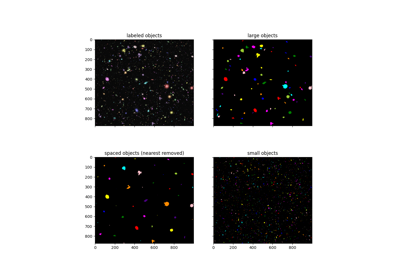
- skimage.measure.label(label_image, background=None, return_num=False, connectivity=None)[ソース]#
整数配列の連結領域にラベルを付けます。
2 つのピクセルは、隣接していて同じ値を持っている場合に接続されます。2D では、1 接続または 2 接続のいずれかの意味で隣接している可能性があります。値は、ピクセル/ボクセルを隣接と見なすために考慮する直交ホップの最大数を指します。
1-connectivity 2-connectivity diagonal connection close-up [ ] [ ] [ ] [ ] [ ] | \ | / | <- hop 2 [ ]--[x]--[ ] [ ]--[x]--[ ] [x]--[ ] | / | \ hop 1 [ ] [ ] [ ] [ ]
- パラメーター:
- label_imagedtype int の ndarray
ラベル付けする画像。
- backgroundint, optional
この値を持つすべてのピクセルを背景ピクセルとみなし、0 としてラベル付けします。デフォルトでは、0 値のピクセルは背景ピクセルとみなされます。
- return_numbool, optional
割り当てられたラベルの数を返すかどうか。
- connectivityint, optional
ピクセル/ボクセルを隣接と見なすために考慮する直交ホップの最大数。受け入れられる値の範囲は 1 から input.ndim までです。
Noneの場合、input.ndimの完全な接続が使用されます。
- 戻り値:
- labelsdtype int の ndarray
ラベル付き配列。すべての接続された領域に同じ整数値が割り当てられています。
- numint, optional
ラベルの数。これは最大ラベルインデックスに等しく、return_num が
Trueの場合にのみ返されます。
参考文献
[1]Christophe Fiorio and Jens Gustedt, “Two linear time Union-Find strategies for image processing”, Theoretical Computer Science 154 (1996), pp. 165-181.
[2]Kensheng Wu, Ekow Otoo and Arie Shoshani, “Optimizing connected component labeling algorithms”, Paper LBNL-56864, 2005, Lawrence Berkeley National Laboratory (University of California), http://repositories.cdlib.org/lbnl/LBNL-56864
例
>>> import numpy as np >>> x = np.eye(3).astype(int) >>> print(x) [[1 0 0] [0 1 0] [0 0 1]] >>> print(label(x, connectivity=1)) [[1 0 0] [0 2 0] [0 0 3]] >>> print(label(x, connectivity=2)) [[1 0 0] [0 1 0] [0 0 1]] >>> print(label(x, background=-1)) [[1 2 2] [2 1 2] [2 2 1]] >>> x = np.array([[1, 0, 0], ... [1, 1, 5], ... [0, 0, 0]]) >>> print(label(x)) [[1 0 0] [1 1 2] [0 0 0]]
- skimage.measure.manders_coloc_coeff(image0, image1_mask, mask=None)[ソース]#
2 つのチャネル間のマンダース共局在化係数。
- パラメーター:
- image0(M, N) ndarray
チャネル A の画像。すべてのピクセル値は非負である必要があります。
- image1_mask(M, N) dtype bool の ndarray
チャネル B の関心領域のセグメント化されたバイナリマスク。
image0と同じ次元でなければなりません。- mask(M, N) dtype bool の ndarray, optional
この関心領域マスク内の
image0のピクセル値のみが計算に含まれます。image0と同じ次元でなければなりません。
- 戻り値:
- mccfloat
マンダース共局在化係数。
注記
マンダース共局在化係数(MCC)は、あるチャネル(チャネル A)の全強度の中で、2 番目のチャネル(チャネル B)のセグメント化された領域内にある割合です [1]。共局在化がない場合は 0、完全な共局在化の場合は 1 の範囲になります。M1 および M2 とも呼ばれます。
MCC は、細胞内区画内の特定のタンパク質の共局在化を測定するためによく使用されます。通常、チャネル B のセグメンテーションマスクは、ピクセル値を MCC 計算に含めるために超える必要のあるしきい値を設定することによって生成されます。この実装では、チャネル B マスクは引数
image1_maskとして提供され、ユーザーが事前に正確なセグメンテーション方法を決定できるようになります。実装された方程式は次のとおりです。
\[r = \frac{\sum A_{i,coloc}}{\sum A_i}\]- ここで
\(A_i\) は
image0の \(i^{th}\) ピクセルの値です。 \(A_{i,coloc} = A_i\) (もし \(Bmask_i > 0\)) \(Bmask_i\) はmaskの \(i^{th}\) ピクセルの値です。
MCC はノイズに敏感で、最初のチャネルの拡散信号が値を膨らませます。MCC を計算する前に、画像の焦点が合っていない光や背景光を取り除くために処理する必要があります [2]。
参考文献
[1]Manders, E.M.M., Verbeek, F.J. and Aten, J.A. (1993), 二色共焦点画像におけるオブジェクトの共局在の測定。Journal of Microscopy, 169: 375-382. https://doi.org/10.1111/j.1365-2818.1993.tb03313.x https://imagej.net/media/manders.pdf
[2]Dunn, K. W., Kamocka, M. M., & McDonald, J. H. (2011). 生物顕微鏡における共局在を評価するための実践的なガイド。American journal of physiology. Cell physiology, 300(4), C723–C742. https://doi.org/10.1152/ajpcell.00462.2010
- skimage.measure.manders_overlap_coeff(image0, image1, mask=None)[ソース]#
マンダースのオーバーラップ係数
- パラメーター:
- image0(M, N) ndarray
チャネル A の画像。すべてのピクセル値は非負である必要があります。
- image1(M, N) ndarray
チャンネルBの画像。すべてのピクセル値は非負である必要があります。
image0と同じ次元を持つ必要があります。- mask(M, N) dtype bool の ndarray, optional
この関心領域マスク内の
image0とimage1のピクセル値のみが計算に含まれます。image0と同じ次元を持つ必要があります。
- 戻り値:
- moc: float
2つの画像間のピクセル強度のマンダースのオーバーラップ係数。
注記
マンダースのオーバーラップ係数(MOC)は、次の式で与えられます[1]
\[r = \frac{\sum A_i B_i}{\sqrt{\sum A_i^2 \sum B_i^2}}\]- ここで
\(A_i\)は
image0の\(i\)番目のピクセルの値であり、\(B_i\)はimage1の\(i\)番目のピクセルの値です
共局在がない場合は0、すべてのピクセルの完全な共局在の場合は1の範囲になります。
MOCはピクセルの強度を考慮せず、両方のチャンネルで正の値を持つピクセルの割合のみを考慮します[R2208c1a5d6e1-2]_ [3]。その有用性は、共発生と相関の両方の違いに応じて変化するため、特定のMOC値は広範囲の共局在パターンを示す可能性があるため、批判されています[4] [5]。
参考文献
[1]Manders, E.M.M., Verbeek, F.J. and Aten, J.A. (1993), 二色共焦点画像におけるオブジェクトの共局在の測定。Journal of Microscopy, 169: 375-382. https://doi.org/10.1111/j.1365-2818.1993.tb03313.x https://imagej.net/media/manders.pdf
[2]Dunn, K. W., Kamocka, M. M., & McDonald, J. H. (2011). 生物顕微鏡における共局在を評価するための実践的なガイド。American journal of physiology. Cell physiology, 300(4), C723–C742. https://doi.org/10.1152/ajpcell.00462.2010
[3]Bolte, S. and Cordelières, F.P. (2006), 光顕微鏡における細胞内共局在解析へのガイド付きツアー。Journal of Microscopy, 224: 213-232. https://doi.org/10.1111/j.1365-2818.2006.01
[4]Adler J, Parmryd I. (2010), 相関による共局在の定量化:ピアソンの相関係数は、マンダースのオーバーラップ係数よりも優れています。Cytometry A. Aug;77(8):733-42.https://doi.org/10.1002/cyto.a.20896
[5]Adler, J, Parmryd, I. 共局在の定量化:マンダースのオーバーラップ係数を破棄する理由。Cytometry. 2021; 99: 910– 920. https://doi.org/10.1002/cyto.a.24336
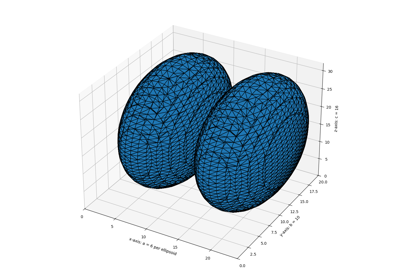
- skimage.measure.marching_cubes(volume, level=None, *, spacing=(1.0, 1.0, 1.0), gradient_direction='descent', step_size=1, allow_degenerate=True, method='lewiner', mask=None)[ソース]#
3Dボリュームデータ内の表面を検出するためのマーチングキューブアルゴリズム。
Lorensenらのアプローチ[2]とは対照的に、Lewinerらのアルゴリズムは高速であり、曖昧さを解消し、トポロジー的に正しい結果を保証します。したがって、このアルゴリズムは一般的に優れた選択肢です。
- パラメーター:
- volume(M, N, P) ndarray
等値面を見つけるための入力データボリューム。必要に応じて内部でfloat32に変換されます。
- levelfloat, optional
volume内の等値面を検索するための等高線値。指定されていないかNoneの場合、volの最小値と最大値の平均が使用されます。- spacing長さ3のfloatのタプル、オプション
volumeと同様に、NumPy配列のインデックス付けの次元(M、N、P)に対応する空間次元のボクセル間隔。- gradient_direction文字列、オプション
メッシュが関心のあるオブジェクトに向かって勾配降下する等値面から生成されたか(デフォルト)、または反対に、左手ルールを考慮して生成されたかを制御します。2つのオプションは次のとおりです。* descent:オブジェクトが外部より大きかった * ascent:外部がオブジェクトより大きかった
- step_size整数、オプション
ボクセル単位のステップサイズ。デフォルトは1。ステップサイズが大きいほど結果は高速になりますが、粗くなります。ただし、結果は常にトポロジー的に正しいものになります。
- allow_degenerateブール値、オプション
最終結果に縮退した(つまり、面積ゼロの)三角形を許可するかどうか。デフォルトはTrue。Falseの場合、縮退した三角形は削除され、アルゴリズムの速度が低下します。
- method: {‘lewiner’, ‘lorensen’}, optional
Lewinerらの方法とLorensenらの方法のどちらを使用するか。
- mask(M, N, P) 配列、オプション
ブール配列。マーチングキューブアルゴリズムは、True要素のみで計算されます。これにより、インターフェイスがボリュームM、N、Pの特定の領域内にある場合(たとえば、キューブの上半分)、計算時間を節約し、有限サーフェス(つまり、キューブの境界で終わらない開いたサーフェス)を計算することもできます。
- 戻り値:
- verts(V, 3) 配列
V個のユニークなメッシュ頂点の空間座標。座標の順序は、入力の
volume(M、N、P)と一致します。allow_degenerateがTrueに設定されている場合、メッシュ内の縮退した三角形の存在により、この配列に重複する頂点が含まれる可能性があります。- faces(F, 3) 配列
vertsからの頂点インデックスを参照して、三角形の面を定義します。このアルゴリズムは特に三角形を出力するため、各面には3つのインデックスがあります。- normals(V, 3) 配列
データから計算された各頂点での法線方向。
- values(V,) 配列
各頂点付近の局所領域におけるデータの最大値の尺度を示します。これは、視覚化ツールでメッシュにカラーマップを適用するために使用できます。
注記
アルゴリズム[1]は、チェルニャエフのマーチングキューブ33アルゴリズムの改良版です。これは効率的なアルゴリズムであり、多くの異なるケースを処理するためにルックアップテーブルを多用し、アルゴリズムを比較的簡単に保ちます。この実装はCythonで記述されており、LewinerのC++実装から移植されています。
このアルゴリズムによって生成された等値面の面積を定量化するには、vertsとfacesを
skimage.measure.mesh_surface_areaに渡します。アルゴリズム出力の視覚化に関して、
mayaviパッケージを使用して、レベル0.0の周りのmyvolumeという名前のボリュームを等高線化するには>>> >> from mayavi import mlab >> verts, faces, _, _ = marching_cubes(myvolume, 0.0) >> mlab.triangular_mesh([vert[0] for vert in verts], [vert[1] for vert in verts], [vert[2] for vert in verts], faces) >> mlab.show()
同様に、
visvisパッケージを使用する場合>>> >> import visvis as vv >> verts, faces, normals, values = marching_cubes(myvolume, 0.0) >> vv.mesh(np.fliplr(verts), faces, normals, values) >> vv.use().Run()
パフォーマンスを向上させるためにメッシュ内の三角形の数を減らすには、
mayaviパッケージを使用したこの例を参照してください。参考文献
[1]Thomas Lewiner, Helio Lopes, Antonio Wilson Vieira and Geovan Tavares. トポロジ保証付きのマーチングキューブケースの効率的な実装。Journal of Graphics Tools 8(2) pp. 1-15 (2003年12月). DOI:10.1080/10867651.2003.10487582
[2]Lorensen, William and Harvey E. Cline. Marching Cubes: A High Resolution 3D Surface Construction Algorithm. Computer Graphics (SIGGRAPH 87 Proceedings) 21(4) July 1987, p. 163-170). DOI:10.1145/37401.37422
- skimage.measure.mesh_surface_area(verts, faces)[ソース]#
頂点と三角形の面が与えられた場合、表面積を計算します。
- パラメーター:
- verts(V, 3) floatの配列
V個のユニークなメッシュ頂点の座標を含む配列。
- faces(F, 3) intの配列
長さ3の整数のリストのリストで、
vertsで提供される頂点座標を参照します。
- 戻り値:
- areafloat
メッシュの表面積。単位は [座標単位] ** 2 となります。
注記
この関数が期待する引数は、
skimage.measure.marching_cubesの最初の2つの出力です。単位が正しい出力を得るためには、skimage.measure.marching_cubesに正しいspacingが渡されていることを確認してください。このアルゴリズムは、提供された
facesがすべて三角形である場合にのみ正しく機能します。
- skimage.measure.moments(image, order=3, *, spacing=None)[ソース]#
特定の次数までのすべての生の画像モーメントを計算します。
- 以下のプロパティは、raw image moments から計算できます。
面積:
M[0, 0]重心: {
M[1, 0] / M[0, 0],M[0, 1] / M[0, 0]}
raw moment は、並進、スケール、回転に対して不変ではないことに注意してください。
- パラメーター:
- image(N[, …]) double または uint8 配列
ラスタライズされた形状を画像として表現したものです。
- orderint, オプション
モーメントの最大次数。デフォルトは 3 です。
- spacing: float のタプル、形状 (ndim,)
画像の各軸に沿ったピクセル間隔。
- 戻り値:
- m(
order + 1,order + 1) 配列 raw image moments。
- m(
参考文献
[1]Wilhelm Burger, Mark Burge. Principles of Digital Image Processing: Core Algorithms. Springer-Verlag, London, 2009.
[2]B. Jähne. Digital Image Processing. Springer-Verlag, Berlin-Heidelberg, 6. edition, 2005.
[3]T. H. Reiss. Recognizing Planar Objects Using Invariant Image Features, from Lecture notes in computer science, p. 676. Springer, Berlin, 1993.
例
>>> image = np.zeros((20, 20), dtype=np.float64) >>> image[13:17, 13:17] = 1 >>> M = moments(image) >>> centroid = (M[1, 0] / M[0, 0], M[0, 1] / M[0, 0]) >>> centroid (14.5, 14.5)
- skimage.measure.moments_central(image, center=None, order=3, *, spacing=None, **kwargs)[ソース]#
特定の次数までのすべての中央画像モーメントを計算します。
中心座標 (cr, cc) は、raw moments から {
M[1, 0] / M[0, 0],M[0, 1] / M[0, 0]} として計算できます。central moment は、並進に対して不変ですが、スケールと回転に対しては不変ではないことに注意してください。
- パラメーター:
- image(N[, …]) double または uint8 配列
ラスタライズされた形状を画像として表現したものです。
- centerfloat のタプル, オプション
画像の重心の座標。これが提供されていない場合は計算されます。
- orderint, オプション
計算されるモーメントの最大次数。
- spacing: float のタプル、形状 (ndim,)
画像の各軸に沿ったピクセル間隔。
- 戻り値:
- mu(
order + 1,order + 1) 配列 central image moments。
- mu(
参考文献
[1]Wilhelm Burger, Mark Burge. Principles of Digital Image Processing: Core Algorithms. Springer-Verlag, London, 2009.
[2]B. Jähne. Digital Image Processing. Springer-Verlag, Berlin-Heidelberg, 6. edition, 2005.
[3]T. H. Reiss. Recognizing Planar Objects Using Invariant Image Features, from Lecture notes in computer science, p. 676. Springer, Berlin, 1993.
例
>>> image = np.zeros((20, 20), dtype=np.float64) >>> image[13:17, 13:17] = 1 >>> M = moments(image) >>> centroid = (M[1, 0] / M[0, 0], M[0, 1] / M[0, 0]) >>> moments_central(image, centroid) array([[16., 0., 20., 0.], [ 0., 0., 0., 0.], [20., 0., 25., 0.], [ 0., 0., 0., 0.]])
- skimage.measure.moments_coords(coords, order=3)[ソース]#
特定の次数までのすべての生の画像モーメントを計算します。
- 以下のプロパティは、raw image moments から計算できます。
面積:
M[0, 0]重心: {
M[1, 0] / M[0, 0],M[0, 1] / M[0, 0]}
raw moment は、並進、スケール、回転に対して不変ではないことに注意してください。
- パラメーター:
- coords(N, D) double または uint8 配列
デカルト空間における D 次元の画像を記述する N 個の点の配列。
- orderint, オプション
モーメントの最大次数。デフォルトは 3 です。
- 戻り値:
- M(
order + 1,order + 1, …) 配列 raw image moments。(D 次元)
- M(
参考文献
[1]Johannes Kilian. Simple Image Analysis By Moments. Durham University, version 0.2, Durham, 2001.
例
>>> coords = np.array([[row, col] ... for row in range(13, 17) ... for col in range(14, 18)], dtype=np.float64) >>> M = moments_coords(coords) >>> centroid = (M[1, 0] / M[0, 0], M[0, 1] / M[0, 0]) >>> centroid (14.5, 15.5)
- skimage.measure.moments_coords_central(coords, center=None, order=3)[ソース]#
特定の次数までのすべての中央画像モーメントを計算します。
- 以下のプロパティは、raw image moments から計算できます。
面積:
M[0, 0]重心: {
M[1, 0] / M[0, 0],M[0, 1] / M[0, 0]}
raw moment は、並進、スケール、回転に対して不変ではないことに注意してください。
- パラメーター:
- coords(N, D) double または uint8 配列
デカルト空間における D 次元の画像を記述する N 個の点の配列。
np.nonzeroによって返される座標のタプルも入力として受け入れられます。- centerfloat のタプル, オプション
画像の重心の座標。これが提供されていない場合は計算されます。
- orderint, オプション
モーメントの最大次数。デフォルトは 3 です。
- 戻り値:
- Mc(
order + 1,order + 1, …) 配列 central image moments。(D 次元)
- Mc(
参考文献
[1]Johannes Kilian. Simple Image Analysis By Moments. Durham University, version 0.2, Durham, 2001.
例
>>> coords = np.array([[row, col] ... for row in range(13, 17) ... for col in range(14, 18)]) >>> moments_coords_central(coords) array([[16., 0., 20., 0.], [ 0., 0., 0., 0.], [20., 0., 25., 0.], [ 0., 0., 0., 0.]])
上記のように、対称的なオブジェクトの場合、オブジェクトの重心または質量中心(デフォルト)を中心にすると、奇数次のモーメント(列1と3、行1と3)はゼロになります。新しい点を追加して対称性を崩すと、これはもはや当てはまりません。
>>> coords2 = np.concatenate((coords, [[17, 17]]), axis=0) >>> np.round(moments_coords_central(coords2), ... decimals=2) array([[17. , 0. , 22.12, -2.49], [ 0. , 3.53, 1.73, 7.4 ], [25.88, 6.02, 36.63, 8.83], [ 4.15, 19.17, 14.8 , 39.6 ]])
画像のモーメントとcentral image momentsは、中心が (0, 0) の場合に(定義上)等価になります。
>>> np.allclose(moments_coords(coords), ... moments_coords_central(coords, (0, 0))) True
- skimage.measure.moments_hu(nu)[ソース]#
Hu の画像モーメントのセットを計算します (2D のみ)。
このモーメントのセットは、並進、スケール、回転に対して不変であることが証明されています。
- パラメーター:
- nu(M, M) 配列
正規化された central image moments。M は >= 4 である必要があります。
- 戻り値:
- nu(7,) 配列
Hu の画像モーメントのセット。
参考文献
[1]M. K. Hu, “Visual Pattern Recognition by Moment Invariants”, IRE Trans. Info. Theory, vol. IT-8, pp. 179-187, 1962
[2]Wilhelm Burger, Mark Burge. Principles of Digital Image Processing: Core Algorithms. Springer-Verlag, London, 2009.
[3]B. Jähne. Digital Image Processing. Springer-Verlag, Berlin-Heidelberg, 6. edition, 2005.
[4]T. H. Reiss. Recognizing Planar Objects Using Invariant Image Features, from Lecture notes in computer science, p. 676. Springer, Berlin, 1993.
例
>>> image = np.zeros((20, 20), dtype=np.float64) >>> image[13:17, 13:17] = 0.5 >>> image[10:12, 10:12] = 1 >>> mu = moments_central(image) >>> nu = moments_normalized(mu) >>> moments_hu(nu) array([0.74537037, 0.35116598, 0.10404918, 0.04064421, 0.00264312, 0.02408546, 0. ])
- skimage.measure.moments_normalized(mu, order=3, spacing=None)[ソース]#
特定の次数までのすべての正規化された中央画像モーメントを計算します。
正規化された central moments は、並進とスケールに対して不変ですが、回転に対しては不変ではないことに注意してください。
- パラメーター:
- mu(M[, …], M) 配列
central image moments。M は
order以上である必要があります。- orderint, オプション
モーメントの最大次数。デフォルトは 3 です。
- spacing: float のタプル、形状 (ndim,)
画像の各軸に沿ったピクセル間隔。
- 戻り値:
- nu(
order + 1``[, ...], ``order + 1) 配列 正規化された central image moments。
- nu(
参考文献
[1]Wilhelm Burger, Mark Burge. Principles of Digital Image Processing: Core Algorithms. Springer-Verlag, London, 2009.
[2]B. Jähne. Digital Image Processing. Springer-Verlag, Berlin-Heidelberg, 6. edition, 2005.
[3]T. H. Reiss. Recognizing Planar Objects Using Invariant Image Features, from Lecture notes in computer science, p. 676. Springer, Berlin, 1993.
例
>>> image = np.zeros((20, 20), dtype=np.float64) >>> image[13:17, 13:17] = 1 >>> m = moments(image) >>> centroid = (m[0, 1] / m[0, 0], m[1, 0] / m[0, 0]) >>> mu = moments_central(image, centroid) >>> moments_normalized(mu) array([[ nan, nan, 0.078125 , 0. ], [ nan, 0. , 0. , 0. ], [0.078125 , 0. , 0.00610352, 0. ], [0. , 0. , 0. , 0. ]])
- skimage.measure.pearson_corr_coeff(image0, image1, mask=None)[ソース]#
チャネル間のピクセル強度に関するピアソンの相関係数を計算します。
- パラメーター:
- image0(M, N) ndarray
チャネル A の画像。
- image1(M, N) ndarray
チャネル B と相関させるチャネル 2 の画像。
image0と同じ次元である必要があります。- mask(M, N) dtype bool の ndarray, optional
この関心領域マスク内の
image0とimage1のピクセルのみが計算に含まれます。image0と同じ次元を持っている必要があります。
- 戻り値:
- pccfloat
マスクが提供されている場合は、2つの画像間のピクセル強度のピアソンの相関係数。
- p-valuefloat
両側p値。
注記
ピアソンの相関係数(PCC)は、2つの画像のピクセル強度間の線形相関を測定します。その値は、完全な線形負の相関の場合は-1から、完全な線形正の相関の場合は+1の範囲になります。p値の計算では、各入力画像のピクセル強度が正規分布していると仮定しています。
Scipyによるピアソンの相関係数の実装が使用されています。詳細と注意事項については、そちらを参照してください[1]。
\[r = \frac{\sum (A_i - m_A_i) (B_i - m_B_i)} {\sqrt{\sum (A_i - m_A_i)^2 \sum (B_i - m_B_i)^2}}\]- ここで
\(A_i\) は、
image0の\(i\)番目のピクセルの値です。\(B_i\) は、image1の\(i\)番目のピクセルの値です。\(m_A_i\) は、image0のピクセル値の平均です。\(m_B_i\) は、image1のピクセル値の平均です。
PCCの値が低いことは、必ずしも2つのチャネル強度間に相関がないことを意味するわけではなく、線形相関がないだけです。2つのチャネルのピクセル強度を2D散布図にプロットし、非線形相関が視覚的に識別される場合は、スピアマンの順位相関を使用することをお勧めします[2]。また、相関に関心があるのか、共起に関心があるのかを検討してください。後者の場合は、セグメンテーションマスクを使用する手法(例えば、MCCまたは交差係数)がより適切かもしれません[3] [4]。
PCCはこれらの測定に敏感であるため、画像の関連セクション(例えば、細胞または特定の細胞小器官)のみのマスクを提供し、ノイズを除去することが重要です[3] [4]。
参考文献
[3] (1,2)Dunn, K. W., Kamocka, M. M., & McDonald, J. H. (2011). 生物顕微鏡における共局在を評価するための実践的なガイド。American journal of physiology. Cell physiology, 300(4), C723–C742. https://doi.org/10.1152/ajpcell.00462.2010
[4] (1,2)Bolte, S. and Cordelières, F.P. (2006), A guided tour into subcellular colocalization analysis in light microscopy. Journal of Microscopy, 224: 213-232. https://doi.org/10.1111/j.1365-2818.2006.01706.x
- skimage.measure.perimeter(image, neighborhood=4)[source]#
バイナリ画像内のすべてのオブジェクトの合計周囲長を計算します。
- パラメーター:
- image(M, N) ndarray
バイナリ入力画像。
- neighborhood4または8、オプション
境界ピクセル決定のための近傍連結性。これは輪郭の計算に使用されます。近傍が大きいほど、周囲長が計算される境界が広がります。
- 戻り値:
- perimeterfloat
バイナリ画像内のすべてのオブジェクトの合計周囲長。
参考文献
[1]K. Benkrid, D. Crookes. Design and FPGA Implementation of a Perimeter Estimator. The Queen’s University of Belfast. http://www.cs.qub.ac.uk/~d.crookes/webpubs/papers/perimeter.doc
例
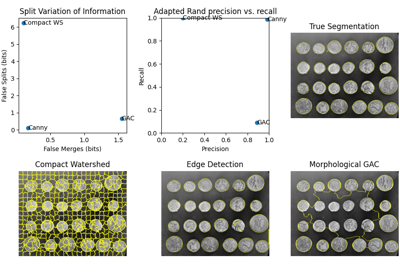
>>> from skimage import data, util >>> from skimage.measure import label >>> # coins image (binary) >>> img_coins = data.coins() > 110 >>> # total perimeter of all objects in the image >>> perimeter(img_coins, neighborhood=4) 7796.867... >>> perimeter(img_coins, neighborhood=8) 8806.268...
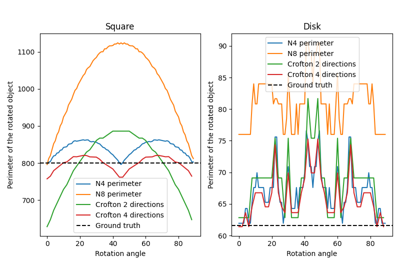
- skimage.measure.perimeter_crofton(image, directions=4)[source]#
バイナリ画像内のすべてのオブジェクトの合計クロフトン周囲長を計算します。
- パラメーター:
- image(M, N) ndarray
入力画像。画像がバイナリでない場合、ゼロより大きいすべての値がオブジェクトと見なされます。
- directions2または4、オプション
クロフトン周囲長の近似に使用される方向の数。デフォルトでは4が使用されます。2よりも正確であるはずです。計算時間はどちらの場合も同じです。
- 戻り値:
- perimeterfloat
バイナリ画像内のすべてのオブジェクトの合計周囲長。
注記
この測定は、積分幾何学からの尺度であるクロフトンの公式[1]に基づいています。これは、すべての方向に沿った二重積分を介した一般的な曲線長の評価として定義されています。離散空間では、2つまたは4つの方向で非常に良好な近似が得られ、より複雑な形状の場合は4つの方が2つよりも正確です。
perimeter()と同様に、この関数は連続空間における周囲長の近似値を返します。参考文献
[2]S. Rivollier. Analyse d’image geometrique et morphometrique par diagrammes de forme et voisinages adaptatifs generaux. PhD thesis, 2010. Ecole Nationale Superieure des Mines de Saint-Etienne. https://tel.archives-ouvertes.fr/tel-00560838
例
>>> from skimage import data, util >>> from skimage.measure import label >>> # coins image (binary) >>> img_coins = data.coins() > 110 >>> # total perimeter of all objects in the image >>> perimeter_crofton(img_coins, directions=2) 8144.578... >>> perimeter_crofton(img_coins, directions=4) 7837.077...
- skimage.measure.points_in_poly(points, verts)[source]#
点がポリゴン内にあるかどうかをテストします。
- パラメーター:
- points(K, 2) array
入力点、
(x, y)。- verts(L, 2) array
ポリゴンの頂点。時計回りまたは反時計回りにソートされます。最初の点は重複しても(しなくても)構いません。
- 戻り値:
- mask(K,) array of bool
対応する点がポリゴン内にある場合はTrue。
- skimage.measure.profile_line(image, src, dst, linewidth=1, order=None, mode='reflect', cval=0.0, *, reduce_func=<function mean>)[source]#
スキャンラインに沿って測定された画像の強度プロファイルを返します。
- パラメーター:
- imagendarray, shape (M, N[, C])
画像。グレースケール(2D配列)またはマルチチャネル(3D配列。最後の軸にチャネル情報が含まれます)。
- srcarray_like, shape (2,)
スキャンラインの開始点の座標。
- dstarray_like, shape (2,)
スキャンラインの終了点の座標。目的点は、標準のnumpyインデックスとは対照的に、プロファイルに含まれています。
- linewidthint, optional
ラインに垂直なスキャンの幅
- order{0, 1, 2, 3, 4, 5}のint, optional
スプライン補間の次数。デフォルトは、image.dtypeがboolの場合は0、それ以外の場合は1です。次数は0〜5の範囲である必要があります。詳細については、
skimage.transform.warpを参照してください。- mode{‘constant’, ‘nearest’, ‘reflect’, ‘mirror’, ‘wrap’}, optional
画像の範囲外にある値を計算する方法。
- cvalfloat, optional
modeが「constant」の場合、画像の外部で使用する定数値。- reduce_funccallable、オプション
linewidth> 1の場合に、profile_lineの方向に垂直なピクセル値の集計を計算するために使用される関数。Noneに設定すると、削減されていない配列が返されます。
- 戻り値:
- return_valuearray
スキャンラインに沿った強度プロファイル。プロファイルの長さは、計算されたスキャンラインの長さのceilです。
例
>>> x = np.array([[1, 1, 1, 2, 2, 2]]) >>> img = np.vstack([np.zeros_like(x), x, x, x, np.zeros_like(x)]) >>> img array([[0, 0, 0, 0, 0, 0], [1, 1, 1, 2, 2, 2], [1, 1, 1, 2, 2, 2], [1, 1, 1, 2, 2, 2], [0, 0, 0, 0, 0, 0]]) >>> profile_line(img, (2, 1), (2, 4)) array([1., 1., 2., 2.]) >>> profile_line(img, (1, 0), (1, 6), cval=4) array([1., 1., 1., 2., 2., 2., 2.])
目的点は、標準のnumpyインデックスとは対照的に、プロファイルに含まれています。例:
>>> profile_line(img, (1, 0), (1, 6)) # The final point is out of bounds array([1., 1., 1., 2., 2., 2., 2.]) >>> profile_line(img, (1, 0), (1, 5)) # This accesses the full first row array([1., 1., 1., 2., 2., 2.])
異なるreduce_func入力の場合
>>> profile_line(img, (1, 0), (1, 3), linewidth=3, reduce_func=np.mean) array([0.66666667, 0.66666667, 0.66666667, 1.33333333]) >>> profile_line(img, (1, 0), (1, 3), linewidth=3, reduce_func=np.max) array([1, 1, 1, 2]) >>> profile_line(img, (1, 0), (1, 3), linewidth=3, reduce_func=np.sum) array([2, 2, 2, 4])
reduce_funcがNoneの場合、またはreduce_funcが各ピクセル値を個別に処理する場合、削減されていない配列が返されます。>>> profile_line(img, (1, 2), (4, 2), linewidth=3, order=0, ... reduce_func=None) array([[1, 1, 2], [1, 1, 2], [1, 1, 2], [0, 0, 0]]) >>> profile_line(img, (1, 0), (1, 3), linewidth=3, reduce_func=np.sqrt) array([[1. , 1. , 0. ], [1. , 1. , 0. ], [1. , 1. , 0. ], [1.41421356, 1.41421356, 0. ]])
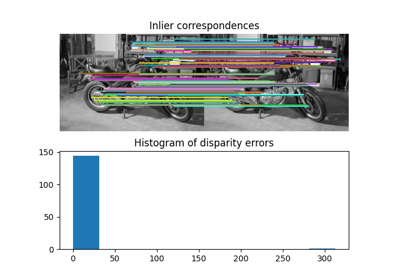
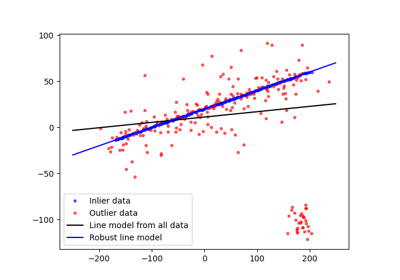
- skimage.measure.ransac(data, model_class, min_samples, residual_threshold, is_data_valid=None, is_model_valid=None, max_trials=100, stop_sample_num=inf, stop_residuals_sum=0, stop_probability=1, rng=None, initial_inliers=None)[ソース]#
RANSAC(ランダムサンプルコンセンサス)アルゴリズムを使用して、データにモデルを適合させます。
RANSACは、完全なデータセットからインライアのサブセットを使用してパラメータをロバストに推定するための反復アルゴリズムです。各反復では、次のタスクを実行します。
元のデータから
min_samples個のランダムサンプルを選択し、データセットが有効かどうかを確認します(is_data_validを参照)。ランダムサブセットに対してモデルを推定し(
model_cls.estimate(*data[random_subset])、推定されたモデルが有効かどうかを確認します(is_model_validを参照)。推定されたモデルへの残差を計算して(
model_cls.residuals(*data))、すべてのデータをインライアまたはアウトライアとして分類します。残差がresidual_thresholdよりも小さいすべてのデータサンプルはインライアとみなされます。インライアサンプルの数が最大の場合、推定されたモデルを最良のモデルとして保存します。現在の推定モデルのインライア数が同じである場合は、残差の合計が少ない場合にのみ最良のモデルとみなされます。
これらのステップは、最大回数実行されるか、特別な停止条件の1つが満たされるまで実行されます。最終モデルは、以前に決定された最良モデルのすべてのインライアサンプルを使用して推定されます。
- パラメーター:
- data[list, tuple of] (N, …) array
モデルが適合されるデータセット。ここで、Nはデータ点の数であり、残りの次元はモデルの要件によって異なります。モデルクラスが複数の入力データ配列(例:
skimage.transform.AffineTransformのソース座標と変換先座標)を必要とする場合、オプションでタプルまたはリストとして渡すことができます。この場合、関数estimate(*data)、residuals(*data)、is_model_valid(model, *random_data)およびis_data_valid(*random_data)は、すべてのデータ配列を別々の引数として取る必要があることに注意してください。- model_classobject
次のオブジェクトメソッドを持つオブジェクト
success = estimate(*data)residuals(*data)
ここで、
successは、モデルの推定が成功したかどうかを示します(成功の場合はTrueまたはNone、失敗の場合はFalse)。- min_samplesint in range (0, N)
モデルを適合させるためのデータ点の最小数。
- residual_thresholdfloat 0より大きい
データ点がインライアとして分類されるための最大距離。
- is_data_validfunction, optional
この関数は、モデルを適合させる前に、ランダムに選択されたデータを使用して呼び出されます:
is_data_valid(*random_data)。- is_model_validfunction, optional
この関数は、推定されたモデルとランダムに選択されたデータを使用して呼び出されます:
is_model_valid(model, *random_data)。- max_trialsint, optional
ランダムサンプル選択の最大反復回数。
- stop_sample_numint, optional
少なくともこの数のインライアが見つかった場合、反復を停止します。
- stop_residuals_sumfloat, optional
残差の合計がこの閾値以下の場合、反復を停止します。
- stop_probabilityfloat in range [0, 1], optional
RANSAC反復は、現在の最良モデルのインライア率と試行回数に応じて、少なくとも1つのアウトライアフリーのトレーニングデータセットが
probability >= stop_probabilityでサンプリングされた場合に停止します。これには、少なくともN個のサンプル(試行)を生成する必要があります。N >= log(1 - probability) / log(1 - e**m)
ここで、probability(信頼度)は通常、0.99のような高い値に設定され、eはサンプル総数に対する現在のインライアの割合であり、mはmin_samplesの値です。
- rng{
numpy.random.Generator, int}, optional 擬似乱数ジェネレーター。デフォルトでは、PCG64ジェネレーターが使用されます(
numpy.random.default_rng()を参照)。rngがintの場合、ジェネレーターをシードするために使用されます。- initial_inliersarray-like of bool, shape (N,), optional
モデル推定のための初期サンプル選択
- 戻り値:
- modelobject
最大コンセンサスセットを持つ最良のモデル。
- inliers(N,) array
Trueと分類されたインライアのブールマスク。
参考文献
[1]「RANSAC」、Wikipedia、https://en.wikipedia.org/wiki/RANSAC
例
傾きのない楕円データを生成し、ノイズを追加します
>>> t = np.linspace(0, 2 * np.pi, 50) >>> xc, yc = 20, 30 >>> a, b = 5, 10 >>> x = xc + a * np.cos(t) >>> y = yc + b * np.sin(t) >>> data = np.column_stack([x, y]) >>> rng = np.random.default_rng(203560) # do not copy this value >>> data += rng.normal(size=data.shape)
いくつかの欠陥データを追加します
>>> data[0] = (100, 100) >>> data[1] = (110, 120) >>> data[2] = (120, 130) >>> data[3] = (140, 130)
利用可能なすべてのデータを使用して楕円モデルを推定します
>>> model = EllipseModel() >>> model.estimate(data) True >>> np.round(model.params) array([ 72., 75., 77., 14., 1.])
RANSACを使用して楕円モデルを推定します
>>> ransac_model, inliers = ransac(data, EllipseModel, 20, 3, max_trials=50) >>> abs(np.round(ransac_model.params)) array([20., 30., 10., 6., 2.]) >>> inliers array([False, False, False, False, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True], dtype=bool) >>> sum(inliers) > 40 True
RANSACは、幾何変換をロバストに推定するために使用できます。このセクションでは、絶対数ではなく、総サンプル数の割合を使用する方法についても示します。
>>> from skimage.transform import SimilarityTransform >>> rng = np.random.default_rng() >>> src = 100 * rng.random((50, 2)) >>> model0 = SimilarityTransform(scale=0.5, rotation=1, ... translation=(10, 20)) >>> dst = model0(src) >>> dst[0] = (10000, 10000) >>> dst[1] = (-100, 100) >>> dst[2] = (50, 50) >>> ratio = 0.5 # use half of the samples >>> min_samples = int(ratio * len(src)) >>> model, inliers = ransac( ... (src, dst), ... SimilarityTransform, ... min_samples, ... 10, ... initial_inliers=np.ones(len(src), dtype=bool), ... ) >>> inliers array([False, False, False, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True])
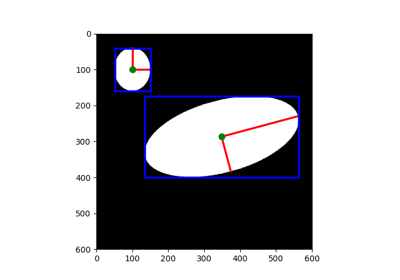
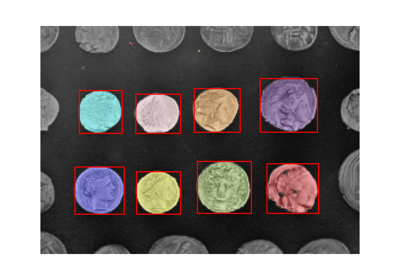
- skimage.measure.regionprops(label_image, intensity_image=None, cache=True, *, extra_properties=None, spacing=None, offset=None)[ソース]#
ラベル付き画像領域のプロパティを測定します。
- パラメーター:
- label_image(M, N[, P]) ndarray
ラベル付けされた入力画像。値が0のラベルは無視されます。
バージョン 0.14.1 で変更:以前は、
label_imageはnumpy.squeezeによって処理されていたため、任意の数のシングルトン次元が許可されていました。これにより、シングルトン次元を持つ画像の一貫性のない処理が行われました。古い動作を復元するには、regionprops(np.squeeze(label_image), ...)を使用してください。- intensity_image(M, N[, P][, C]) ndarray, optional
ラベル付けされた画像と同じサイズの強度(つまり、入力)画像。オプションで、マルチチャネルデータ用の追加次元も含まれます。現在、この追加チャネル次元が存在する場合、最後の軸である必要があります。デフォルトはNoneです。
バージョン 0.18.0 で変更:チャネル用の追加次元を提供できる機能が追加されました。
- cachebool, optional
計算されたプロパティをキャッシュするかどうかを決定します。キャッシュされたプロパティの場合、計算ははるかに高速になりますが、メモリ消費量が増加します。
- extra_propertiesIterable of callables
skimageに含まれていない追加のプロパティ計算関数を追加します。プロパティの名前は関数名から派生し、dtypeは小さなサンプルで関数を呼び出すことによって推論されます。追加のプロパティの名前が既存のプロパティの名前と衝突する場合、追加のプロパティは表示されず、UserWarningが発行されます。プロパティ計算関数は、最初の引数として領域マスクを取る必要があります。プロパティが強度画像を必要とする場合、2番目の引数として強度画像を受け入れる必要があります。
- spacing: float のタプル、形状 (ndim,)
画像の各軸に沿ったピクセル間隔。
- offsetarray-like of int, shape
(label_image.ndim,), optional ラベル画像の原点(「左上」隅)の座標。通常は([0, ]0, 0)ですが、より大きなボリューム内のサブボリュームのregionpropsを取得する場合は異なる場合があります。
- 戻り値:
- propertieslist of RegionProperties
各項目は1つのラベル付けされた領域を表し、以下に示す属性を使用してアクセスできます。
参考
注記
次のプロパティには、属性またはキーとしてアクセスできます
- areafloat
領域の面積。つまり、ピクセル面積でスケーリングされた領域のピクセル数。
- area_bboxfloat
バウンディングボックスの面積。つまり、ピクセル面積でスケーリングされたバウンディングボックスのピクセル数。
- area_convexfloat
凸包画像の面積。これは、領域を囲む最小の凸ポリゴンです。
- area_filledfloat
すべての穴が埋められた領域の面積。
- axis_major_lengthfloat
領域と同じ正規化された2番目の中央モーメントを持つ楕円の長軸の長さ。
- axis_minor_lengthfloat
領域と同じ正規化された2次中心モーメントを持つ楕円の短軸の長さ。
- bboxtuple
バウンディングボックス
(min_row, min_col, max_row, max_col)。バウンディングボックスに属するピクセルは、半開区間[min_row; max_row)および[min_col; max_col)にあります。- centroidarray
重心座標タプル
(row, col)。- centroid_localarray
領域のバウンディングボックスを基準とした重心座標タプル
(row, col)。- centroid_weightedarray
強度画像で重み付けされた重心座標タプル
(row, col)。- centroid_weighted_localarray
領域のバウンディングボックスを基準とし、強度画像で重み付けされた重心座標タプル
(row, col)。- coords_scaled(K, 2) ndarray
spacingでスケールされた領域の座標リスト(row, col)。- coords(K, 2) ndarray
領域の座標リスト
(row, col)。- eccentricityfloat
領域と同じ2次モーメントを持つ楕円の離心率。離心率は、焦点距離(焦点間の距離)を長軸の長さで割ったものです。値は [0, 1) の範囲です。0の場合、楕円は円になります。
- equivalent_diameter_areafloat
領域と同じ面積を持つ円の直径。
- euler_numberint
非ゼロピクセルの集合のオイラー特性。連結成分の数から穴の数を引いたものとして計算されます(入力の ndim 連結性)。3Dでは、連結成分の数に穴の数を足し、そこからトンネルの数を引いたものになります。
- extentfloat
領域内のピクセルとバウンディングボックス全体のピクセルの比率。
area / (rows * cols)として計算されます。- feret_diameter_maxfloat
find_contoursによって決定された領域の凸包輪郭周りの点間の最長距離として計算される最大フェレ径。[5]- image(H, J) ndarray
バウンディングボックスと同じサイズを持つスライスされたバイナリ領域画像。
- image_convex(H, J) ndarray
バウンディングボックスと同じサイズを持つバイナリ凸包画像。
- image_filled(H, J) ndarray
バウンディングボックスと同じサイズを持つ、穴が埋められたバイナリ領域画像。
- image_intensityndarray
領域バウンディングボックス内の画像。
- inertia_tensorndarray
質量を中心とした領域の慣性テンソル。
- inertia_tensor_eigvalstuple
降順に並べられた慣性テンソルの固有値。
- intensity_maxfloat
領域内で最も大きい強度を持つ値。
- intensity_meanfloat
領域内の平均強度を持つ値。
- intensity_minfloat
領域内で最も小さい強度を持つ値。
- intensity_stdfloat
領域内の強度の標準偏差。
- labelint
ラベル付き入力画像内のラベル。
- moments(3, 3) ndarray
3次までの空間モーメント
m_ij = sum{ array(row, col) * row^i * col^j }
ここで、和は領域の
row、col座標にわたります。- moments_central(3, 3) ndarray
3次までの中央モーメント(並進不変)
mu_ij = sum{ array(row, col) * (row - row_c)^i * (col - col_c)^j }
ここで、和は領域の
row、col座標にわたります。row_cおよびcol_cは領域の重心の座標です。- moments_hutuple
Hu モーメント(並進、スケール、回転不変)。
- moments_normalized(3, 3) ndarray
3次までの正規化モーメント(並進およびスケール不変)
nu_ij = mu_ij / m_00^[(i+j)/2 + 1]
ここで、
m_00はゼロ次の空間モーメントです。- moments_weighted(3, 3) ndarray
強度画像の3次までの空間モーメント
wm_ij = sum{ array(row, col) * row^i * col^j }
ここで、和は領域の
row、col座標にわたります。- moments_weighted_central(3, 3) ndarray
強度画像の3次までの中央モーメント(並進不変)
wmu_ij = sum{ array(row, col) * (row - row_c)^i * (col - col_c)^j }
ここで、和は領域の
row、col座標にわたります。row_cおよびcol_cは領域の重み付けされた重心の座標です。- moments_weighted_hutuple
強度画像のHu モーメント(並進、スケール、回転不変)。
- moments_weighted_normalized(3, 3) ndarray
強度画像の3次までの正規化モーメント(並進およびスケール不変)
wnu_ij = wmu_ij / wm_00^[(i+j)/2 + 1]
ここで、
wm_00はゼロ次の空間モーメント(強度で重み付けされた面積)です。- num_pixelsint
前景ピクセルの数。
- orientationfloat
領域と同じ2次モーメントを持つ楕円の長軸と0番目の軸(行)の間の角度。
-pi/2からpi/2の範囲で、反時計回り。- perimeterfloat
4連結性を使用して、境界ピクセルの中心を通る線として輪郭を近似するオブジェクトの周囲長。
- perimeter_croftonfloat
4方向のクロフトン式で近似されたオブジェクトの周囲長。
- slicetuple of slices
ソース画像からオブジェクトを抽出するためのスライス。
- solidityfloat
領域内のピクセルと凸包画像のピクセルの比率。
各領域はイテレーションもサポートしているため、次のようにできます。
for prop in region: print(prop, region[prop])
参考文献
[1]Wilhelm Burger, Mark Burge. Principles of Digital Image Processing: Core Algorithms. Springer-Verlag, London, 2009.
[2]B. Jähne. Digital Image Processing. Springer-Verlag, Berlin-Heidelberg, 6. edition, 2005.
[3]T. H. Reiss. Recognizing Planar Objects Using Invariant Image Features, from Lecture notes in computer science, p. 676. Springer, Berlin, 1993.
[5]W. Pabst, E. Gregorová. Characterization of particles and particle systems, pp. 27-28. ICT Prague, 2007. https://old.vscht.cz/sil/keramika/Characterization_of_particles/CPPS%20_English%20version_.pdf
例
>>> from skimage import data, util >>> from skimage.measure import label, regionprops >>> img = util.img_as_ubyte(data.coins()) > 110 >>> label_img = label(img, connectivity=img.ndim) >>> props = regionprops(label_img) >>> # centroid of first labeled object >>> props[0].centroid (22.72987986048314, 81.91228523446583) >>> # centroid of first labeled object >>> props[0]['centroid'] (22.72987986048314, 81.91228523446583)
extra_propertiesとして関数を渡すことで、カスタム測定を追加します>>> from skimage import data, util >>> from skimage.measure import label, regionprops >>> import numpy as np >>> img = util.img_as_ubyte(data.coins()) > 110 >>> label_img = label(img, connectivity=img.ndim) >>> def pixelcount(regionmask): ... return np.sum(regionmask) >>> props = regionprops(label_img, extra_properties=(pixelcount,)) >>> props[0].pixelcount 7741 >>> props[1]['pixelcount'] 42
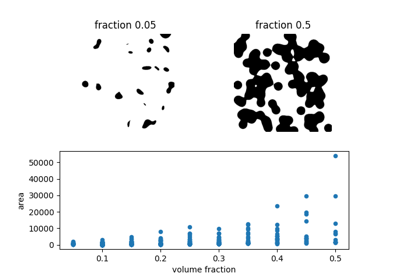
- skimage.measure.regionprops_table(label_image, intensity_image=None, properties=('label', 'bbox'), *, cache=True, separator='-', extra_properties=None, spacing=None)[source]#
画像プロパティを計算し、pandas互換のテーブルとして返します。
テーブルは、列名を値配列にマッピングする辞書です。詳細については、以下の「注釈」セクションを参照してください。
バージョン 0.16 で追加されました。
- パラメーター:
- label_image(M, N[, P]) ndarray
ラベル付けされた入力画像。値が0のラベルは無視されます。
- intensity_image(M, N[, P][, C]) ndarray, optional
ラベル付き画像と同じサイズの強度(つまり、入力)画像。オプションで、マルチチャネルデータ用の追加次元を含めることもできます。チャネル次元が存在する場合、それは最後の軸でなければなりません。デフォルトは None です。
バージョン 0.18.0 で変更:チャネル用の追加次元を提供できる機能が追加されました。
- propertiestuple または str のリスト、オプション
結果の辞書に含めるプロパティ。利用可能なプロパティのリストについては、
regionprops()を参照してください。領域の ID を追跡するため、「label」を追加することを忘れないでください。- cachebool, optional
計算されたプロパティをキャッシュするかどうかを決定します。キャッシュされたプロパティの場合、計算ははるかに高速になりますが、メモリ消費量が増加します。
- separatorstr, オプション
OBJECT_COLUMNS にリストされていない非スカラープロパティの場合、各要素は独自の列に表示され、その要素のインデックスは、このセパレータでプロパティ名と区切られます。たとえば、2D 領域の慣性テンソルは、
inertia_tensor-0-0、inertia_tensor-0-1、inertia_tensor-1-0、およびinertia_tensor-1-1の4つの列に表示されます(セパレータが-の場合)。オブジェクト列は、列の数がオブジェクトによって変化するため、このように分割できない列です。たとえば、
imageおよびcoordsなどです。- extra_propertiesIterable of callables
skimageに含まれていない追加のプロパティ計算関数を追加します。プロパティの名前は関数名から派生し、dtypeは小さなサンプルで関数を呼び出すことによって推論されます。追加のプロパティの名前が既存のプロパティの名前と衝突する場合、追加のプロパティは表示されず、UserWarningが発行されます。プロパティ計算関数は、最初の引数として領域マスクを取る必要があります。プロパティが強度画像を必要とする場合、2番目の引数として強度画像を受け入れる必要があります。
- spacing: float のタプル、形状 (ndim,)
画像の各軸に沿ったピクセル間隔。
- 戻り値:
- out_dictdict
プロパティ名をそのプロパティの値の配列(領域ごとに1つの値)にマッピングする辞書。この辞書は、pandas
DataFrameへの入力として使用して、プロパティ名をフレーム内の列に、領域を行にマッピングできます。画像に領域がない場合、配列の長さは 0 になりますが、正しい型になります。
注記
各列には、スカラープロパティ、オブジェクトプロパティ、または多次元配列の要素のいずれかが含まれます。
「eccentricity」などの各領域のスカラー値を持つプロパティは、そのプロパティ名をキーとして持つ float または int 配列として表示されます。
「centroid」(すべての重心は、領域のサイズに関係なく、3D 画像では 3 つの要素を持つ)など、特定の画像ディメンションに対して固定サイズの多次元プロパティは、{property_name}{separator}{element_num}(1D プロパティの場合)、{property_name}{separator}{elem_num0}{separator}{elem_num1}(2D プロパティの場合)などのように、その数の列に分割されます。
「image」(領域のサイズによって変化する領域の画像など)のように、サイズが固定されていない多次元プロパティの場合、オブジェクト配列が使用され、対応するプロパティ名がキーとして使用されます。
例
>>> from skimage import data, util, measure >>> image = data.coins() >>> label_image = measure.label(image > 110, connectivity=image.ndim) >>> props = measure.regionprops_table(label_image, image, ... properties=['label', 'inertia_tensor', ... 'inertia_tensor_eigvals']) >>> props {'label': array([ 1, 2, ...]), ... 'inertia_tensor-0-0': array([ 4.012...e+03, 8.51..., ...]), ... ..., 'inertia_tensor_eigvals-1': array([ 2.67...e+02, 2.83..., ...])}
結果の辞書は、インストールされている場合、pandasに直接渡して、クリーンなDataFrameを取得できます。
>>> import pandas as pd >>> data = pd.DataFrame(props) >>> data.head() label inertia_tensor-0-0 ... inertia_tensor_eigvals-1 0 1 4012.909888 ... 267.065503 1 2 8.514739 ... 2.834806 2 3 0.666667 ... 0.000000 3 4 0.000000 ... 0.000000 4 5 0.222222 ... 0.111111
[5行 x 7列]
組み込みのプロパティとして提供されない特徴を測定したい場合は、カスタム関数を定義し、それらを
extra_propertiesとして渡すことができます。たとえば、領域内の強度四分位数を測定するカスタム関数を作成できます。>>> from skimage import data, util, measure >>> import numpy as np >>> def quartiles(regionmask, intensity): ... return np.percentile(intensity[regionmask], q=(25, 50, 75)) >>> >>> image = data.coins() >>> label_image = measure.label(image > 110, connectivity=image.ndim) >>> props = measure.regionprops_table(label_image, intensity_image=image, ... properties=('label',), ... extra_properties=(quartiles,)) >>> import pandas as pd >>> pd.DataFrame(props).head() label quartiles-0 quartiles-1 quartiles-2 0 1 117.00 123.0 130.0 1 2 111.25 112.0 114.0 2 3 111.00 111.0 111.0 3 4 111.00 111.5 112.5 4 5 112.50 113.0 114.0
- skimage.measure.shannon_entropy(image, base=2)[ソース]#
画像のシャノンエントロピーを計算します。
シャノンエントロピーは、S = -sum(pk * log(pk))として定義されます。ここで、pkは値kのピクセルの頻度/確率です。
- パラメーター:
- image(M, N) ndarray
グレースケールの入力画像。
- basefloat, オプション
使用する対数の底。
- 戻り値:
- entropyfloat
注記
返される値は、base=2の場合はビットまたはシャノン(Sh)、base=np.eの場合は自然単位(nat)、base=10の場合はハートレー(Hart)で測定されます。
参考文献
例
>>> from skimage import data >>> from skimage.measure import shannon_entropy >>> shannon_entropy(data.camera()) 7.231695011055706
- skimage.measure.subdivide_polygon(coords, degree=2, preserve_ends=False)[ソース]#
Bスプラインを使用したポリゴン曲線の細分化。
結果の曲線は常に元のポリゴンの凸包内にあることに注意してください。円形のポリゴンは細分化後も閉じられたままです。
- パラメーター:
- coords(K, 2) 配列
座標配列。
- degree{1, 2, 3, 4, 5, 6, 7}, オプション
Bスプラインの次数。デフォルトは2です。
- preserve_endsbool, オプション
非円形のポリゴンの最初と最後の座標を保持します。デフォルトはFalseです。
- 戻り値:
- coords(L, 2) 配列
細分化された座標配列。
参考文献
- class skimage.measure.CircleModel[ソース]#
ベース:
BaseModel2D円の総最小二乗推定量。
円の関数モデルは次のとおりです
r**2 = (x - xc)**2 + (y - yc)**2
この推定量は、すべての点から円までの二乗距離を最小化します。
min{ sum((r - sqrt((x_i - xc)**2 + (y_i - yc)**2))**2) }
パラメーターを解くには、最小3点が必要です。
- 属性:
- paramstuple
円モデルのパラメータは、
xc、yc、rの順です。
注記
推定は、[1]に示されている球面推定の2Dバージョンを使用して実行されます。
参考文献
[1]Jekel, Charles F. Obtaining non-linear orthotropic material models for pvc-coated polyester via inverse bubble inflation. Thesis (MEng), Stellenbosch University, 2016. Appendix A, pp. 83-87. https://hdl.handle.net/10019.1/98627
例
>>> t = np.linspace(0, 2 * np.pi, 25) >>> xy = CircleModel().predict_xy(t, params=(2, 3, 4)) >>> model = CircleModel() >>> model.estimate(xy) True >>> tuple(np.round(model.params, 5)) (2.0, 3.0, 4.0) >>> res = model.residuals(xy) >>> np.abs(np.round(res, 9)) array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])
- estimate(data)[ソース]#
総最小二乗法を使用してデータから円モデルを推定します。
- パラメーター:
- data(N, 2) 配列
それぞれ
(x, y)座標を持つN個の点。
- 戻り値:
- successbool
モデルの推定が成功した場合はTrue。
- class skimage.measure.EllipseModel[ソース]#
ベース:
BaseModel2D楕円の総最小二乗推定量。
楕円の関数モデルは次のとおりです
xt = xc + a*cos(theta)*cos(t) - b*sin(theta)*sin(t) yt = yc + a*sin(theta)*cos(t) + b*cos(theta)*sin(t) d = sqrt((x - xt)**2 + (y - yt)**2)
ここで、
(xt, yt)は、(x, y)に最も近い楕円上の点です。したがって、dは点から楕円までの最短距離です。推定量は最小二乗最小化に基づいています。最適な解は直接計算され、反復は不要です。これにより、シンプルで安定した堅牢なフィッティング方法が得られます。
params属性には、次の順序でパラメータが含まれています。xc, yc, a, b, theta
- 属性:
- paramstuple
楕円モデルのパラメータは、
xc、yc、a、b、thetaの順です。
例
>>> xy = EllipseModel().predict_xy(np.linspace(0, 2 * np.pi, 25), ... params=(10, 15, 8, 4, np.deg2rad(30))) >>> ellipse = EllipseModel() >>> ellipse.estimate(xy) True >>> np.round(ellipse.params, 2) array([10. , 15. , 8. , 4. , 0.52]) >>> np.round(abs(ellipse.residuals(xy)), 5) array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])
- estimate(data)[ソース]#
総最小二乗法を使用してデータから楕円モデルを推定します。
- パラメーター:
- data(N, 2) 配列
それぞれ
(x, y)座標を持つN個の点。
- 戻り値:
- successbool
モデルの推定が成功した場合はTrue。
参考文献
[1]Halir, R.; Flusser, J. “Numerically stable direct least squares fitting of ellipses”. In Proc. 6th International Conference in Central Europe on Computer Graphics and Visualization. WSCG (Vol. 98, pp. 125-132).
- class skimage.measure.LineModelND[ソース]#
ベース:
BaseModelN次元線の総最小二乗推定量。
通常の最小二乗線推定とは対照的に、この推定量は、推定された線への点の直交距離を最小化します。
線は、次のベクトル方程式に従って、点(原点)と単位ベクトル(方向)によって定義されます
X = origin + lambda * direction
- 属性:
- paramstuple
線モデルのパラメータは、
origin、directionの順です。
例
>>> x = np.linspace(1, 2, 25) >>> y = 1.5 * x + 3 >>> lm = LineModelND() >>> lm.estimate(np.stack([x, y], axis=-1)) True >>> tuple(np.round(lm.params, 5)) (array([1.5 , 5.25]), array([0.5547 , 0.83205])) >>> res = lm.residuals(np.stack([x, y], axis=-1)) >>> np.abs(np.round(res, 9)) array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]) >>> np.round(lm.predict_y(x[:5]), 3) array([4.5 , 4.562, 4.625, 4.688, 4.75 ]) >>> np.round(lm.predict_x(y[:5]), 3) array([1. , 1.042, 1.083, 1.125, 1.167])
- estimate(data)[ソース]#
データから線形モデルを推定します。
これは、与えられたデータ点から推定された線への最短(直交)距離の合計を最小化します。
- パラメーター:
- data(N, dim) 配列
次元 dim >= 2 の空間における N 個の点。
- 戻り値:
- successbool
モデルの推定が成功した場合はTrue。
- predict(x, axis=0, params=None)[ソース]#
推定された線形モデルと、指定された軸に直交する超平面との交点を予測します。
- パラメーター:
- x(n, 1) 配列
軸に沿った座標。
- axisint
線と交差する超平面に直交する軸。
- params(2,) 配列, オプション
オプションのカスタムパラメータセット(
origin,direction)の形式。
- 戻り値:
- data(n, m) 配列
予測された座標。
- 例外:
- ValueError
線が指定された軸と平行な場合。
- predict_x(y, params=None)[ソース]#
推定されたモデルを使用して、2D線のx座標を予測します。
エイリアス:
predict(y, axis=1)[:, 0]
- パラメーター:
- y配列
y座標。
- params(2,) 配列, オプション
オプションのカスタムパラメータセット(
origin,direction)の形式。
- 戻り値:
- x配列
予測されたx座標。