`skimage.metrics`#

画像に対応するメトリック、例えば、距離メトリック、類似度など。

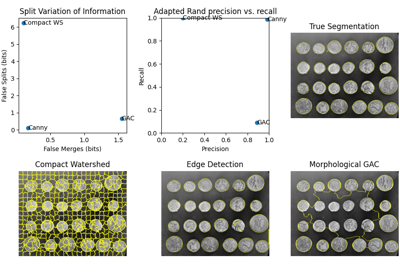
`adapted_rand_error`	SNEMI3D コンテストで定義されているように、適合ランダムエラーを計算します。
`contingency_table`	一致したセグメンテーションのすべての領域の分割表を返します。
`hausdorff_distance`	指定された画像の非ゼロ要素間のハウスドルフ距離を計算します。
`hausdorff_pair`	指定された画像の非ゼロ要素間のハウスドルフ距離にある点のペアを返します。
`mean_squared_error`	2つの画像間の平均二乗誤差を計算します。
`normalized_mutual_information`	正規化相互情報量 (NMI) を計算します。
`normalized_root_mse`	2つの画像間の正規化二乗平均平方根誤差 (NRMSE) を計算します。
`peak_signal_noise_ratio`	画像のピーク信号対雑音比 (PSNR) を計算します。
`structural_similarity`	2つの画像間の平均構造類似性指数を計算します。
`variation_of_information`	VI に関連付けられた対称条件付きエントロピーを返します。

skimage.metrics.adapted_rand_error(image_true=None, image_test=None, *, table=None, ignore_labels=(0,), alpha=0.5)[ソース]#

SNEMI3D コンテストで定義されているように、適合ランダムエラーを計算します。 [1]

パラメータ:

image_true整数のndarray: im_testと同じ形状の正解ラベル画像。
image_test整数のndarray: テスト画像。
tablecrs形式のscipy.sparse配列、オプション: skimage.evaluate.contingency_tableで構築された分割表。Noneの場合、オンザフライで計算されます。
ignore_labels整数のシーケンス、オプション: 無視するラベル。これらの値のいずれかでラベル付けされた真の画像の部分は、スコアにカウントされません。
alpha浮動小数点数、オプション: 適合ランダムエラー計算における適合率と再現率に与えられる相対的な重み。

戻り値:

are浮動小数点数: 適合ランダムエラー。
prec浮動小数点数: 適合ランダム適合率: これは、テストラベル画像と真の画像の両方で同じラベルを持つピクセルのペアの数を、テスト画像の数で割ったものです。
rec浮動小数点数: 適合ランダム再現率: これは、テストラベル画像と真の画像の両方で同じラベルを持つピクセルのペアの数を、真の画像の数で割ったものです。

注記

真のセグメンテーションでラベル0のピクセルは、スコアでは無視されます。

適合ランダムエラーは次のように計算されます

\(1 - \frac{\sum_{ij} p_{ij}^{2}}{\alpha \sum_{k} s_{k}^{2} + (1-\alpha)\sum_{k} t_{k}^{2}}\)。ここで、\(p_{ij}\) はピクセルがテスト画像と真の画像の両方で同じラベルを持つ確率、\(t_{k}\) はピクセルが真の画像でラベル \(k\) を持つ確率、\(s_{k}\) はピクセルがテスト画像でラベル \(k\) を持つ確率です。

デフォルトの動作では、適合ランダムエラー計算において適合率と再現率に等しい重みを与えます。alpha = 0 の場合、適合ランダムエラー = 再現率です。alpha = 1 の場合、適合ランダムエラー = 適合率です。

参考文献

[1]

Arganda-Carreras I, Turaga SC, Berger DR, et al. (2015) Crowdsourcing the creation of image segmentation algorithms for connectomics. Front. Neuroanat. 9:142. DOI:10.3389/fnana.2015.00142

セグメンテーションメトリックの評価

skimage.metrics.contingency_table(im_true, im_test, *, ignore_labels=None, normalize=False, sparse_type='matrix')[ソース]#

一致したセグメンテーションのすべての領域の分割表を返します。

パラメータ:

im_true整数のndarray: im_testと同じ形状の正解ラベル画像。
im_test整数のndarray: テスト画像。
ignore_labels整数のシーケンス、オプション: 無視するラベル。これらの値のいずれかでラベル付けされた真の画像の部分は、スコアにカウントされません。
normalizeブール値: 分割表がピクセル数で正規化されるかどうかを決定します。
sparse_type{“matrix”, “array”}、オプション: cont の戻り値の型。 scipy.sparse.csr_array または scipy.sparse.csr_matrix (デフォルト)。

戻り値:

contscipy.sparse.csr_matrix または scipy.sparse.csr_array: 分割表。 cont[i, j] は、im_true で i とラベル付けされ、im_test で j とラベル付けされたボクセルの数と等しくなります。 sparse_type によっては、scipy.sparse.csr_array として返される場合があります。

skimage.metrics.hausdorff_distance(image0, image1, method='standard')[ソース]#

指定された画像の非ゼロ要素間のハウスドルフ距離を計算します。

パラメータ:

**image0, image1**ndarray: True が点の集合に含まれる点を表す配列。両方の配列は同じ形状である必要があります。
**method**{‘standard’, ‘modified’}、オプション、デフォルト = ‘standard’: ハウスドルフ距離の計算に使用するメソッド。 standard は標準ハウスドルフ距離、modified は修正ハウスドルフ距離です。

戻り値:

**distance**浮動小数点数: ユークリッド距離を使用して、image0 と image1 の非ゼロピクセルの座標間のハウスドルフ距離。

注記

ハウスドルフ距離 [1] は、image0 上の任意の点と image1 上のその最近傍点との間の最大距離、およびその逆です。修正ハウスドルフ距離 (MHD) は、Dubuissonらによる以下の研究で、方向付きハウスドルフ距離 (HD) よりも優れた性能を発揮することが示されています [2]。この関数は、前方平均距離と後方平均距離を計算し、2つのうち大きい方を返します。

参考文献

[1]

http://en.wikipedia.org/wiki/Hausdorff_distance

[2]

M. P. Dubuisson and A. K. Jain. A Modified Hausdorff distance for object matching. In ICPR94, pages A:566-568, Jerusalem, Israel, 1994. DOI:10.1109/ICPR.1994.576361 http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.1.8155

例

>>> points_a = (3, 0)
>>> points_b = (6, 0)
>>> shape = (7, 1)
>>> image_a = np.zeros(shape, dtype=bool)
>>> image_b = np.zeros(shape, dtype=bool)
>>> image_a[points_a] = True
>>> image_b[points_b] = True
>>> hausdorff_distance(image_a, image_b)
3.0

ハウスドルフ距離

skimage.metrics.hausdorff_pair(image0, image1)[source]#

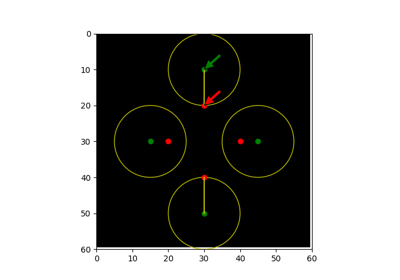
指定された画像の非ゼロ要素間のハウスドルフ距離にある点のペアを返します。

ハウスドルフ距離 [1] は、`image0` 上の任意の点とその `image1` 上の最近傍点との間の最大距離、およびその逆です。

パラメータ:

**image0, image1**ndarray: True が点の集合に含まれる点を表す配列。両方の配列は同じ形状である必要があります。

戻り値:

point_a, point_b配列: ハウスドルフ距離を持つ点のペア。

参考文献

[1]

http://en.wikipedia.org/wiki/Hausdorff_distance

例

>>> points_a = (3, 0)
>>> points_b = (6, 0)
>>> shape = (7, 1)
>>> image_a = np.zeros(shape, dtype=bool)
>>> image_b = np.zeros(shape, dtype=bool)
>>> image_a[points_a] = True
>>> image_b[points_b] = True
>>> hausdorff_pair(image_a, image_b)
(array([3, 0]), array([6, 0]))

ハウスドルフ距離

skimage.metrics.mean_squared_error(image0, image1)[source]#

2つの画像間の平均二乗誤差を計算します。

パラメータ:

**image0, image1**ndarray: 画像。任意の次元数で、同じ形状でなければなりません。

戻り値:

mse浮動小数点数: 平均二乗誤差（MSE）メトリック。

注記

バージョン 0.16 で変更: この関数は `skimage.measure.compare_mse` から `skimage.metrics.mean_squared_error` に名前が変更されました。

構造的類似性指標

J-不変量を用いたデノイザーのキャリブレーションに関する完全なチュートリアル

skimage.metrics.normalized_mutual_information(image0, image1, *, bins=100)[source]#

正規化相互情報量 (NMI) を計算します。

\(A\) と \(B\) の正規化相互情報量は、次式で与えられます。

.. math::

Y(A, B) = frac{H(A) + H(B)}{H(A, B)}

ここで、\(H(X) := - \sum_{x \in X}{x \log x}\) はエントロピーです。

これは、Colin Studholme ら [1] によって画像レジストレーションに有用であると提案されました。 1（完全に無相関の画像値）から 2（正または負に完全に相関した画像値）の範囲です。

パラメータ:

**image0, image1**ndarray: 比較する画像。2 つの入力画像は同じ次元数でなければなりません。
bins整数または整数のシーケンス、オプション: 結合ヒストグラムの各軸に沿ったビンの数。

戻り値:

nmi浮動小数点数: `bins` で指定された粒度で計算された、2 つの配列間の正規化相互情報量。NMI が高いほど、入力画像がより類似していることを意味します。

発生させる:

ValueError: 画像の次元数が同じでない場合。

注記

2 つの入力画像の形状が同じでない場合、小さい方の画像はゼロで埋められます。

参考文献

[1]

C. Studholme, D.L.G. Hill, & D.J. Hawkes (1999). An overlap invariant entropy measure of 3D medical image alignment. Pattern Recognition 32(1):71-86 DOI:10.1016/S0031-3203(98)00091-0

skimage.metrics.normalized_root_mse(image_true, image_test, *, normalization='euclidean')[source]#

2つの画像間の正規化二乗平均平方根誤差 (NRMSE) を計算します。

パラメータ:

image_truendarray

im_test と同じ形状の、真の画像。

image_testndarray

テスト画像。

テスト画像。im_true と同じ形状。

normalization{‘euclidean’, ‘min-max’, ‘mean’}, optional

NRMSE の分母で使用する正規化方法を制御します。文献全体で標準的な正規化方法はありません [1]。ここで利用可能な方法は次のとおりです。
```
NRMSE = RMSE * sqrt(N) / || im_true ||
```
「ユークリッド」: `im_true` の平均ユークリッドノルムで正規化します
```
NRMSE = || im_true - im_test || / || im_true ||.
```
ここで、|| . || はフロベニウスノルムを示し、`N = im_true.size` です。この結果は次の式と同等です
「min-max」: `im_true` の輝度範囲で正規化します。

戻り値:

「平均」: `im_true` の平均で正規化します: nrmse浮動小数点数

注記

NRMSE メトリック。

参考文献

[1]

バージョン 0.16 で変更: この関数は `skimage.measure.compare_nrmse` から `skimage.metrics.normalized_root_mse` に名前が変更されました。

https://en.wikipedia.org/wiki/Root-mean-square_deviation

画像のピーク信号対雑音比 (PSNR) を計算します。

パラメータ:

image_truendarray: im_test と同じ形状の、真の画像。
image_testndarray: テスト画像。
skimage.metrics.peak_signal_noise_ratio(image_true, image_test, *, data_range=None)[source]#: data_range整数、オプション

戻り値:

入力画像のデータ範囲（最小値と最大値の差）。デフォルトでは、これは画像データ型から推定されます。: psnr浮動小数点数

注記

PSNR メトリック。

参考文献

[1]

バージョン 0.16 で変更: この関数は `skimage.measure.compare_psnr` から `skimage.metrics.peak_signal_noise_ratio` に名前が変更されました。

https://en.wikipedia.org/wiki/Peak_signal-to-noise_ratio

単純な画像スティッチングで画像を組み立てる

シフト不変ウェーブレットデノイジング

テクスチャを保持するための非局所平均デノイジング

J-不変量を用いたデノイザーのキャリブレーションに関する完全なチュートリアル

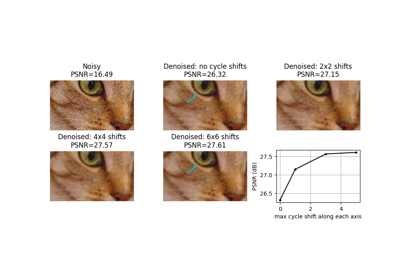
ウェーブレットデノイジング

skimage.metrics.structural_similarity(im1, im2, *, win_size=None, gradient=False, data_range=None, channel_axis=None, gaussian_weights=False, full=False, **kwargs)[source]#

パラメータ:

2 つの画像間の平均構造的類似性指標を計算します。浮動小数点画像の `data_range` パラメータにご注意ください。: im1, im2ndarray
画像。同じ形状の任意の次元数。: win_size整数または None、オプション
比較に使用されるスライドウィンドウの辺の長さ。奇数でなければなりません。`gaussian_weights` が True の場合、これは無視され、ウィンドウサイズは `sigma` に依存します。: gradientブール値、オプション
True の場合、im2 に関する勾配も返します。: data_range浮動小数点数、オプション
入力画像のデータ範囲（最大値と最小値の差）。デフォルトでは、これは画像データ型から推定されます。この推定は、浮動小数点画像データに対して間違っている可能性があります。したがって、このスカラー値を常に明示的に渡すことをお勧めします（以下の注記を参照）。: channel_axis整数または None、オプション

None の場合、画像はグレースケール（シングルチャネル）画像と見なされます。それ以外の場合、このパラメータは配列のどの軸がチャネルに対応するかを示します。
バージョン 0.19 で追加: `channel_axis` は 0.19 で追加されました。: gaussian_weightsブール値、オプション
True の場合、各パッチの平均と分散は、sigma=1.5 の正規化ガウスカーネルによって空間的に重み付けされます。: fullブール値、オプション

戻り値:

True の場合、完全な構造的類似性画像も返します。: mssim浮動小数点数
画像全体の平均構造的類似性指標。: im1とim2の構造的類似度の勾配[2]。これは、gradientがTrueに設定されている場合にのみ返されます。
Sndarray: 完全なSSIM画像。これは、fullがTrueに設定されている場合にのみ返されます。

その他の引数:

use_sample_covariancebool: Trueの場合、共分散をNではなくN-1で正規化します。ここで、Nはスライドウィンドウ内のピクセル数です。
K1float: アルゴリズムパラメータ、K1（小さい定数、[1]を参照）。
K2float: アルゴリズムパラメータ、K2（小さい定数、[1]を参照）。
sigmafloat: gaussian_weightsがTrueの場合のガウス分布の標準偏差。

注記

data_rangeが指定されていない場合、範囲は画像データ型に基づいて自動的に推測されます。ただし、浮動小数点画像データの場合、この推定値は目的の範囲の2倍の値になります。skimage.util.dtype.pyのdtype_rangeは-1から+1までの間隔を定義しているためです。これは、画像データを扱う際に最もよく必要とされる1ではなく、2の推定値を生成します（負の光強度は無意味であるため）。YCbCrのようなカラーデータを扱う場合、これらの範囲はチャネルごとに異なることに注意してください（CbとCrはYの範囲の2倍です）。そのため、この関数への1回の呼び出しでチャネル平均SSIMを計算することはできません。各チャネルで同じ範囲が想定されているためです。

Wangらの実装と一致させるには[1]、gaussian_weightsをTrue、sigmaを1.5、use_sample_covarianceをFalseに設定し、data_range引数を指定します。

バージョン0.16で変更: この関数はskimage.measure.compare_ssimからskimage.metrics.structural_similarityに名前変更されました。

参考文献

[1] (1,2,3)

Wang, Z., Bovik, A. C., Sheikh, H. R., & Simoncelli, E. P. (2004). Image quality assessment: From error visibility to structural similarity. IEEE Transactions on Image Processing, 13, 600-612. https://ece.uwaterloo.ca/~z70wang/publications/ssim.pdf, DOI:10.1109/TIP.2003.819861

[2]

Avanaki, A. N. (2009). Exact global histogram specification optimized for structural similarity. Optical Review, 16, 613-621. arXiv:0901.0065 DOI:10.1007/s10043-009-0119-z

構造的類似性指標

skimage.metrics.variation_of_information(image0=None, image1=None, *, table=None, ignore_labels=())[source]#

VIに関連付けられた対称条件付きエントロピーを返します。[1]

パラメータ:

image0, image1int型のndarray: ラベル画像/セグメンテーション。同じ形状である必要があります。
tablecsr形式のscipy.sparse配列、オプション: skimage.evaluate.contingency_tableで構築された分割表。Noneの場合、skimage.evaluate.contingency_tableで計算されます。指定された場合、エントロピーはこのテーブルから計算され、画像は無視されます。
ignore_labels整数のシーケンス、オプション: 無視するラベル。これらの値のいずれかでラベル付けされた真の画像の部分は、スコアにカウントされません。

戻り値:

vifloat型のndarray、shape (2,): image1|image0とimage0|image1の条件付きエントロピー。

参考文献

[1]

Marina Meilă (2007), Comparing clusterings—an information based distance, Journal of Multivariate Analysis, Volume 98, Issue 5, Pages 873-895, ISSN 0047-259X, DOI:10.1016/j.jmva.2006.11.013.

セグメンテーションメトリックの評価

skimage.metrics#

`skimage.metrics`#