`skimage.filters`#

鮮鋭化、エッジ検出、ランクフィルタ、閾値処理など。

`apply_hysteresis_threshold`	`image`にヒステリシス閾値処理を適用します。
`butterworth`	高周波または低周波の特徴を強調するためにバターワースフィルタを適用します。
`correlate_sparse`	`padded_array`と`kernel`の有効な相互相関を計算します。
`difference_of_gaussians`	`low_sigma`と`high_sigma`のサイズの間の特徴を見つけます。
`farid`	Farid変換を使用してエッジの大きさを求めます。
`farid_h`	Farid変換を使用して画像の水平エッジを求めます。
`farid_v`	Farid変換を使用して画像の垂直エッジを求めます。
`filter_forward`	指定されたフィルタをデータに適用します。
`filter_inverse`	指定されたデータにフィルタを逆方向に適用します。
`frangi`	Frangi血管性フィルタで画像をフィルタリングします。
`gabor`	ガボールフィルタに対する実数と虚数の応答を返します。
`gabor_kernel`	複素数2次元ガボールフィルタカーネルを返します。
`gaussian`	多次元ガウスフィルタ。
`hessian`	ハイブリッドヘシアンフィルタで画像をフィルタリングします。
`laplace`	ラプラス演算子を使用して画像のエッジを求めます。
`median`	画像の局所中央値を返します。
`meijering`	Meijeringニューリティネスフィルタで画像をフィルタリングします。
`prewitt`	Prewitt変換を使用してエッジの大きさを求めます。
`prewitt_h`	Prewitt変換を使用して画像の水平エッジを求めます。
`prewitt_v`	Prewitt変換を使用して画像の垂直エッジを求めます。
`rank_order`	`image`の一意な値の昇順におけるピクセル値のインデックス（ランク順値）である、同じ形状の画像を返します。
`roberts`	Robertsのクロス演算子を使用してエッジの大きさを求めます。
`roberts_neg_diag`	Robertsのクロス演算子を使用して画像のクロスエッジを求めます。
`roberts_pos_diag`	Robertsのクロス演算子を使用して画像のクロスエッジを求めます。
`sato`	Satoチューブネスフィルタで画像をフィルタリングします。
`scharr`	Scharr変換を使用してエッジの大きさを求めます。
`scharr_h`	Scharr変換を使用して画像の水平エッジを求めます。
`scharr_v`	Scharr変換を使用して画像の垂直エッジを求めます。
`sobel`	Sobelフィルタを使用して画像のエッジを求めます。
`sobel_h`	Sobel変換を使用して画像の水平エッジを求めます。
`sobel_v`	Sobel変換を使用して画像の垂直エッジを求めます。
`threshold_isodata`	ISODATA法に基づいて閾値を返します。
`threshold_li`	Liの反復最小交差エントロピー法によって閾値を計算します。
`threshold_local`	局所ピクセル近傍に基づいて閾値マスク画像を計算します。
`threshold_mean`	グレースケール値の平均に基づいて閾値を返します。
`threshold_minimum`	最小値法に基づいて閾値を返します。
`threshold_multiotsu`	複数クラスのOtsuの方法に従って、`image`のグレースケールレベルを分割する`classes`-1個の閾値を生成します。
`threshold_niblack`	配列にNiblack局所閾値を適用します。
`threshold_otsu`	Otsuの方法に基づいて閾値を返します。
`threshold_sauvola`	配列にSauvola局所閾値を適用します。
`threshold_triangle`	三角アルゴリズムに基づいて閾値を返します。
`threshold_yen`	Yenの方法に基づいて閾値を返します。
`try_all_threshold`	異なる閾値化方法の出力を比較する図を返します。
`unsharp_mask`	アンシャープマスキングフィルタ。
`wiener`	最小平均二乗誤差（ウィーナー）逆フィルタ。
`window`	指定されたサイズと次元数のn次元ウィンドウを返します。
`LPIFilter2D`	線形位置不変フィルタ（2次元）
`rank`

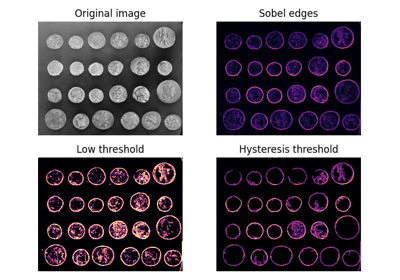
skimage.filters.apply_hysteresis_threshold(image, low, high)[source]#

imageにヒステリシス閾値処理を適用します。

このアルゴリズムは、imageがhighより大きい、またはimageがlowより大きく、かつその領域がhighより大きい領域に接続されている領域を見つけます。

パラメータ：

image(M[, …]) ndarray: グレースケール入力画像。
lowfloat、またはimageと同じ形状の配列: 下限閾値。
highfloat、またはimageと同じ形状の配列: 上限閾値。

戻り値：

thresholded(M[, …]) boolの配列: imageがヒステリシス閾値を超えた場所をTrueで示す配列。

参考文献

[1]

J. Canny. A computational approach to edge detection. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1986; vol. 8, pp.679-698. DOI:10.1109/TPAMI.1986.4767851

例

>>> image = np.array([1, 2, 3, 2, 1, 2, 1, 3, 2])
>>> apply_hysteresis_threshold(image, 1.5, 2.5).astype(int)
array([0, 1, 1, 1, 0, 0, 0, 1, 1])

ヒステリシス閾値処理

ピクセルグラフを使用してオブジェクトの測地線中心を見つける

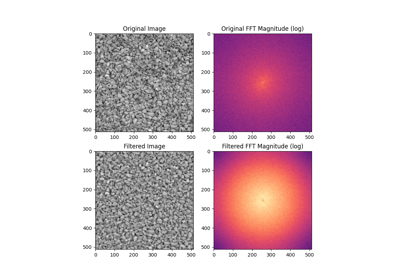
skimage.filters.butterworth(image, cutoff_frequency_ratio=0.005, high_pass=True, order=2.0, channel_axis=None, *, squared_butterworth=True, npad=0)[source]#

高周波または低周波の特徴を強調するためにバターワースフィルタを適用します。

このフィルタはフーリエ領域で定義されています。

パラメータ：

image(M[, N[, …, P]][, C]) ndarray: 入力画像。
cutoff_frequency_ratiofloat, optional: FFTの形状に対してカットオフの位置を決定します。[0, 0.5]の間の値を受け取ります。
high_passbool, optional: ハイパスフィルタを実行するかどうか。Falseの場合、ローパスフィルタが実行されます。
orderfloat, optional: カットオフ付近の傾斜に影響を与えるフィルタの次数。次数が高いほど、周波数空間での傾斜が急になります。
channel_axisint, optional: チャンネル次元がある場合、ここでインデックスを指定します。None（デフォルト）の場合、すべての軸は空間次元と見なされます。
squared_butterworthbool, optional: Trueの場合、バターワースフィルタの2乗が使用されます。詳細は以下の注記を参照してください。
npadint, optional: numpy.padのmode='edge'拡張を使用して、画像の各エッジをnpadピクセルだけパディングします。

戻り値：

resultndarray: バターワースフィルタ処理された画像。

注記

ハイパスフィルタとローパスフィルタを組み合わせることで、バンドパスフィルタを実現できます。境界アーティファクトが目立つ場合は、npadの値を増やすことができます。

画像処理の教科書（例：[1]、[2]）で使用される「バターワースフィルタ」は、[3]、[4]で説明されている従来のバターワースフィルタの2乗であることがよくあります。 squared_butterworthがTrueに設定されている場合、ここでは2乗バージョンが使用されます。ローパスフィルターの場合、2乗バターワースフィルタは次の式で表されます。

\[H_{low}(f) = \frac{1}{1 + \left(\frac{f}{c f_s}\right)^{2n}}\]

ハイパスフィルターの場合、次の式で表されます。

\[H_{hi}(f) = 1 - H_{low}(f)\]

ここで、\(f=\sqrt{\sum_{d=0}^{\mathrm{ndim}} f_{d}^{2}}\)は空間周波数の絶対値、\(f_s\)はサンプリング周波数、\(c\)はcutoff_frequency_ratio、\(n\)はフィルタのorder [1]です。squared_butterworth=Falseの場合、上記の式の平方根が代わりに使用されます。

cutoff_frequency_ratioはサンプリング周波数\(f_s\)で定義されていることに注意してください。FFTスペクトルはナイキスト範囲(\([-f_s/2, f_s/2]\))をカバーするため、cutoff_frequency_ratioの値は0から0.5の間である必要があります。squared_butterworthがtrueの場合、カットオフでの周波数応答（ゲイン）は0.5になり、falseの場合は\(1/\sqrt{2}\)になります。

参考文献

[1] (1,2)

Russ, John C., et al. The Image Processing Handbook, 3rd. Ed. 1999, CRC Press, LLC.

[2]

Birchfield, Stan. Image Processing and Analysis. 2018. Cengage Learning.

[3]

Butterworth, Stephen. “On the theory of filter amplifiers.” Wireless Engineer 7.6 (1930): 536-541.

[4]

https://en.wikipedia.org/wiki/Butterworth_filter

例

グレースケール画像とカラー画像にそれぞれハイパスとローパスのバターワースフィルタを適用します。

>>> from skimage.data import camera, astronaut
>>> from skimage.filters import butterworth
>>> high_pass = butterworth(camera(), 0.07, True, 8)
>>> low_pass = butterworth(astronaut(), 0.01, False, 4, channel_axis=-1)

バターワースフィルタ

skimage.filters.correlate_sparse(image, kernel, mode='reflect')[source]#

padded_arrayとkernelの有効な相互相関を計算します。

この関数は、kernelが大きく、多くのゼロを含む場合、高速です。

相互相関の説明については、scipy.ndimage.correlateを参照してください。

パラメータ：

imagendarray、dtype float、shape (M, N[, …], P): 入力配列。modeが'valid'の場合、この配列は既にパディングされている必要があります。kernelと同じ形状のマージンが取り除かれます。
kernelndarray、dtype float、shape (Q, R[, …], S): 相関付けられるカーネル。 padded_arrayと同じ数の次元を持つ必要があります。高性能のためには、スパース（ゼロ以外のエントリが少ない）である必要があります。
mode文字列、オプション: 有効なモードについては、scipy.ndimage.correlateを参照してください。さらに、mode 'valid'も受け入れられます。この場合、パディングは適用されず、結果は、カーネルが元のデータ全体に完全に含まれるより小さい画像の結果になります。

戻り値：

resultfloatの配列、shape (M, N[, …], P): imageとkernelの相互相関の結果。 mode 'valid'が使用されている場合、結果の形状は(M-Q+1, N-R+1[, …], P-S+1)になります。

skimage.filters.difference_of_gaussians(image, low_sigma, high_sigma=None, *, mode='nearest', cval=0, channel_axis=None, truncate=4.0)[source]#

low_sigmaとhigh_sigmaのサイズの間の特徴を見つけます。

この関数は、多次元配列にバンドパスフィルタを適用するために、ガウシアン差分法を使用します。入力配列は、異なるシグマの2つのガウシアンカーネルでぼかし処理され、2つの中間的なフィルタリングされた画像が生成されます。その後、よりぼかしの強い画像が、ぼかしの弱い画像から減算されます。したがって、最終的な出力画像では、高周波成分はシグマの小さいガウシアンによって減衰され、低周波成分は、よりぼかしの強い中間画像に存在するため、除去されます。

パラメータ：

imagendarray: フィルタリングする入力配列。
low_sigmaスカラーまたはスカラーのシーケンス: すべての軸にわたるシグマの小さいガウシアンカーネルの標準偏差。標準偏差は、シーケンスとして各軸に与えられるか、単一の数字として与えられます。単一の数字が与えられた場合は、その数字がすべての軸の標準偏差値として使用されます。
high_sigmaスカラーまたはスカラーのシーケンス、オプション（デフォルトはNone）: すべての軸にわたるシグマの大きいガウシアンカーネルの標準偏差。標準偏差は、シーケンスとして各軸に与えられるか、単一の数字として与えられます。単一の数字が与えられた場合は、その数字がすべての軸の標準偏差値として使用されます。Noneが指定されている場合（デフォルト）、すべての軸のシグマは1.6 * low_sigmaとして計算されます。
mode{'reflect', 'constant', 'nearest', 'mirror', 'wrap'}、オプション: modeパラメータは、配列の境界の処理方法を決定します。ここで、cvalは、modeが'constant'の場合の値です。デフォルトは'nearest'です。
cvalスカラー、オプション: modeが'constant'の場合、入力の端を超えて埋め込む値。デフォルトは0.0です。
channel_axisintまたはNone、オプション: Noneの場合、画像はグレースケール（シングルチャンネル）画像と見なされます。それ以外の場合は、このパラメータは、配列のどの軸がチャネルに対応するかを示します。

バージョン0.19で追加: channel_axisは0.19で追加されました。
truncatefloat、オプション（デフォルトは4.0）: この標準偏差の倍数でフィルタを打ち切ります。

戻り値：

filtered_imagendarray: フィルタリングされた配列。

こちらも参照してください

skimage.feature.blob_dog

注記

この関数は、high_sigmaで指定されたシグマを持つガウシアンカーネルでフィルタリングされた配列を、low_sigmaで指定されたシグマを持つガウシアンカーネルでフィルタリングされた配列から減算します。high_sigmaの値は、常にlow_sigmaの対応する値以上である必要があります。そうでない場合、ValueErrorが発生します。

high_sigmaがNoneの場合、high_sigmaの値は、low_sigmaの対応する値の1.6倍として計算されます。この比率は、もともとMarrとHildreth（1980）[1]によって提案され、エッジとブロブの検出に使用されるガウシアンの反転ラプラシアンを近似する際に一般的に使用されます。

入力画像は、img_as_floatの規約に従って変換されます。

シグマ値を除き、すべてのパラメータは両方のフィルタに使用されます。

参考文献

[1]

Marr, D. and Hildreth, E. Theory of Edge Detection. Proc. R. Soc. Lond. Series B 207, 187-217 (1980). https://doi.org/10.1098/rspb.1980.0020

例

単純なガウシアン差分フィルタをカラー画像に適用します。

>>> from skimage.data import astronaut
>>> from skimage.filters import difference_of_gaussians
>>> filtered_image = difference_of_gaussians(astronaut(), 2, 10,
...                                          channel_axis=-1)

ガウシアン差分フィルタで近似されたガウシアンのラプラシアンフィルタを適用します。

>>> filtered_image = difference_of_gaussians(astronaut(), 2,
...                                          channel_axis=-1)

各軸に異なるシグマ値を使用して、グレースケール画像にガウシアン差分フィルタを適用します。

>>> from skimage.data import camera
>>> filtered_image = difference_of_gaussians(camera(), (2,5), (3,20))

登録のための極座標変換と対数極座標変換の使用

ガウシアン差分によるバンドパスフィルタリング

skimage.filters.farid(image, mask=None, *, axis=None, mode='reflect', cval=0.0)[source]#

Farid変換を使用してエッジの大きさを求めます。

パラメータ：

image配列

入力画像。

maskbool値の配列、オプション

出力画像をこのマスクにクリップします。(mask=0 の値は 0 に設定されます。)

axisint または int のシーケンス、オプション

この軸に沿ってエッジフィルタを計算します。指定しない場合、エッジの大きさが計算されます。これは次のように定義されます。

farid_mag = np.sqrt(sum([farid(image, axis=i)**2
                         for i in range(image.ndim)]) / image.ndim)

axis がシーケンスの場合も、大きさが計算されます。

mode文字列または文字列のシーケンス、オプション

畳み込みの境界モード。scipy.ndimage.convolve を参照して、モードの説明を確認してください。これは、単一の境界モード、または軸ごとの境界モードのいずれかです。

cval浮動小数点数、オプション

mode が 'constant' の場合、これは画像データの境界外の値に使用される定数です。

戻り値：

output浮動小数点数の配列: Farid エッジマップ。

こちらも参照してください

farid_h、farid_v: 水平および垂直エッジ検出。
scharr、sobel、prewitt、skimage.feature.canny

注記

水平方向と垂直方向の微分の二乗の和の平方根をとって、方向にあまり影響されない大きさを得ます。Scharr 演算子と同様に、この演算子は回転不変性の制約を考慮して設計されています。

参考文献

[1]

Farid, H. and Simoncelli, E. P.、 “Differentiation of discrete multidimensional signals”, IEEE Transactions on Image Processing 13(4): 496-508, 2004. DOI:10.1109/TIP.2004.823819

[2]

Wikipedia、 “Farid and Simoncelli Derivatives.” 閲覧可能: <https://en.wikipedia.org/wiki/Image_derivatives#Farid_and_Simoncelli_Derivatives>

例

>>> from skimage import data
>>> camera = data.camera()
>>> from skimage import filters
>>> edges = filters.farid(camera)

skimage.filters.farid_h(image, *, mask=None)[source]#

Farid変換を使用して画像の水平エッジを求めます。

パラメータ：

image2次元配列: 処理対象の画像。
mask2次元配列、オプション: 適用範囲を特定の領域に制限するためのオプションマスク。マスク領域を囲むピクセルもマスクされ、マスク領域が結果に影響することを防ぎます。

戻り値：

output2次元配列: Farid エッジマップ。

注記

カーネルは、[1] の 5 タップ重みを使用して構築されました。

参考文献

[1]

Farid, H. and Simoncelli, E. P.、 “Differentiation of discrete multidimensional signals”, IEEE Transactions on Image Processing 13(4): 496-508, 2004. DOI:10.1109/TIP.2004.823819

[2]

Farid, H. and Simoncelli, E. P. “Optimally rotation-equivariant directional derivative kernels”, In: 7th International Conference on Computer Analysis of Images and Patterns, Kiel, Germany. Sep, 1997.

エッジオペレータ

skimage.filters.farid_v(image, *, mask=None)[source]#

Farid変換を使用して画像の垂直エッジを求めます。

パラメータ：

image2次元配列: 処理対象の画像。
mask2次元配列、オプション: 適用範囲を特定の領域に制限するためのオプションマスク。マスク領域を囲むピクセルもマスクされ、マスク領域が結果に影響することを防ぎます。

戻り値：

output2次元配列: Farid エッジマップ。

注記

カーネルは、[1] の 5 タップ重みを使用して構築されました。

参考文献

[1]

Farid, H. and Simoncelli, E. P.、 “Differentiation of discrete multidimensional signals”, IEEE Transactions on Image Processing 13(4): 496-508, 2004. DOI:10.1109/TIP.2004.823819

エッジオペレータ

skimage.filters.filter_forward(data, impulse_response=None, filter_params=None, predefined_filter=None)[source]#

指定されたフィルタをデータに適用します。

パラメータ：

data(M, N) ndarray: 入力データ。
impulse_response呼び出し可能 f(r, c, **filter_params): フィルタのインパルス応答。LPIFilter2D.__init__ を参照。
filter_params辞書、オプション: impulse_response 関数に追加のキーワードパラメータ。

その他のオプションパラメータ：

predefined_filterLPIFilter2D: 同じフィルタを異なる画像に対して複数回適用する必要がある場合、LPIFilter2D を構築し、ここで指定します。

例

正規化されていないガウスフィルタ

>>> def filt_func(r, c, sigma=1):
...     return np.exp(-(r**2 + c**2)/(2 * sigma**2))
>>>
>>> from skimage import data
>>> filtered = filter_forward(data.coins(), filt_func)

skimage.filters.filter_inverse(data, impulse_response=None, filter_params=None, max_gain=2, predefined_filter=None)[source]#

指定されたデータにフィルタを逆方向に適用します。

パラメータ：

data(M, N) ndarray: 入力データ。
impulse_response呼び出し可能 f(r, c, **filter_params): フィルタのインパルス応答。LPIFilter2D を参照。 predifined_filter が提供されていない限り、これは必須の引数です。
filter_params辞書、オプション: impulse_response 関数に追加のキーワードパラメータ。
max_gain浮動小数点数、オプション: フィルタゲインを制限します。多くの場合、フィルタにはゼロが含まれており、逆フィルタのゲインが無限大になる可能性があります。高ゲインはアーティファクトの増幅を引き起こすため、保守的な制限が推奨されます。

その他のオプションパラメータ：

predefined_filterLPIFilter2D、オプション: 同じフィルタを異なる画像に対して複数回適用する必要がある場合、LPIFilter2D を構築し、ここで指定します。

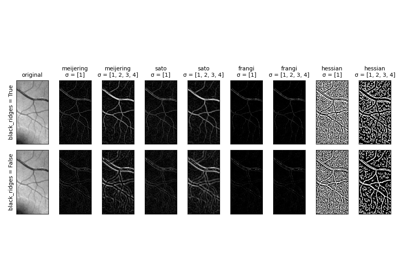
skimage.filters.frangi(image, sigmas=range(1, 10, 2), scale_range=None, scale_step=None, alpha=0.5, beta=0.5, gamma=None, black_ridges=True, mode='reflect', cval=0)[source]#

Frangi血管性フィルタで画像をフィルタリングします。

このフィルタは、連続した尾根（例：血管、しわ、川）を検出するために使用できます。そのようなオブジェクトを含む画像全体の割合を計算するために使用できます。

2次元および3次元画像のみに定義されています。[1]で説明されている方法に従って、ヘッシアンの固有値を計算して、画像領域の血管との類似性を計算します。

パラメータ：

image(M, N[, P]) ndarray: 入力画像データを含む配列。
sigmasfloat のイテラブル、オプション: フィルタのスケールとして使用されるシグマ値 (例: np.arange(scale_range[0], scale_range[1], scale_step))
scale_rangefloat の 2 要素タプル、オプション: 使用されるシグマ値の範囲。
scale_stepfloat、オプション: シグマ値の間隔。
alphafloat、オプション: 平板状構造からのずれに対するフィルタの感度を調整する Frangi 補正定数。
betafloat、オプション: ブロブ状構造からのずれに対するフィルタの感度を調整する Frangi 補正定数。
gammafloat、オプション: 高分散/テクスチャ/構造領域に対するフィルタの感度を調整する Frangi 補正定数。デフォルトの None は、最大ヘッセノルムの半分を使用します。
black_ridgesboolean、オプション: True の場合 (デフォルト)、黒色の隆線を検出します。False の場合、白色の隆線を検出します。
mode{'constant', 'reflect', 'wrap', 'nearest', 'mirror'}、オプション: 画像境界外の値の処理方法。
cval浮動小数点数、オプション: mode 'constant' と共に使用される、画像境界外の値。

戻り値：

out(M, N[, P]) ndarray: フィルタリングされた画像 (すべてのスケールにわたるピクセルの最大値)。

こちらも参照してください

meijering
sato
hessian

注記

このフィルタの以前のバージョンは、Marc Schrijver (2001年11月)、D. J. Kroon, University of Twente (2009年5月) [2]、および D. G. Ellis (2017年1月) [3] によって実装されました。

参考文献

[1]

Frangi, A. F., Niessen, W. J., Vincken, K. L., & Viergever, M. A. (1998,). Multiscale vessel enhancement filtering. In International Conference on Medical Image Computing and Computer-Assisted Intervention (pp. 130-137). Springer Berlin Heidelberg. DOI:10.1007/BFb0056195

[2]

Kroon, D. J.: Hessian based Frangi vesselness filter.

[3]

Ellis, D. G.: ellisdg/frangi3d

リッジ演算子

skimage.filters.gabor(image, frequency, theta=0, bandwidth=1, sigma_x=None, sigma_y=None, n_stds=3, offset=0, mode='reflect', cval=0)[source]#

ガボールフィルタに対する実数と虚数の応答を返します。

ガボールフィルタカーネルの実数部と虚数部は画像に適用され、応答は配列のペアとして返されます。

ガボールフィルタは、正弦波平面波で変調されたガウスカーネルを持つ線形フィルタです。ガボールフィルタの周波数と方向の表現は、人間の視覚システムのものと似ています。ガボールフィルタバンクは、コンピュータビジョンと画像処理で一般的に使用されます。特に、エッジ検出とテクスチャ分類に適しています。

パラメータ：

image2次元配列: 入力画像。
frequencyfloat: 調和関数の空間周波数。ピクセル単位で指定します。
thetafloat、オプション: ラジアン単位の方向。0 の場合、調和関数は x 方向にあります。
bandwidthfloat、オプション: フィルタによって捉えられる帯域幅。帯域幅が固定されている場合、sigma_x と sigma_y は周波数の増加とともに減少します。この値は、sigma_x と sigma_y がユーザーによって設定されている場合は無視されます。
sigma_x, sigma_yfloat、オプション: x 方向と y 方向の標準偏差。これらの方向は、回転 *前* のカーネルに適用されます。theta = pi/2 の場合、カーネルは 90 度回転するため、sigma_x は *垂直* 方向を制御します。
n_stdsスカラー、オプション: カーネルの線形サイズは、n_stds (デフォルトは 3) 標準偏差です。
offsetfloat、オプション: ラジアン単位の調和関数の位相オフセット。
mode{'constant', 'nearest', 'reflect', 'mirror', 'wrap'}、オプション: ndi.convolve に渡される、カーネルで画像を畳み込むために使用されるモード。
cvalスカラー、オプション: 畳み込みの mode が 'constant' の場合、入力の端を超えて埋め込む値。このパラメータは ndi.convolve に渡されます。

戻り値：

real, imag配列: ガボールフィルタカーネルの実数部と虚数部を使用してフィルタリングされた画像。画像は入力画像と同じ次元です。

参考文献

[1]

https://en.wikipedia.org/wiki/Gabor_filter

[2]

https://web.archive.org/web/20180127125930/http://mplab.ucsd.edu/tutorials/gabor.pdf

例

>>> from skimage.filters import gabor
>>> from skimage import data
>>> from matplotlib import pyplot as plt  

>>> image = data.coins()
>>> # detecting edges in a coin image
>>> filt_real, filt_imag = gabor(image, frequency=0.6)
>>> fix, ax = plt.subplots()  
>>> ax.imshow(filt_real)      
>>> plt.show()                

>>> # less sensitivity to finer details with the lower frequency kernel
>>> filt_real, filt_imag = gabor(image, frequency=0.1)
>>> fig, ax = plt.subplots()  
>>> ax.imshow(filt_real)      
>>> plt.show()                

skimage.filters.gabor_kernel(frequency, theta=0, bandwidth=1, sigma_x=None, sigma_y=None, n_stds=3, offset=0, dtype=<class 'numpy.complex128'>)[source]#

複素数2次元ガボールフィルタカーネルを返します。

ガボールカーネルは、複素調和関数で変調されたガウスカーネルです。調和関数は、虚数の正弦関数と実数の余弦関数で構成されます。空間周波数は、調和波の長さとガウスカーネルの標準偏差に反比例します。帯域幅も標準偏差に反比例します。

パラメータ：

frequencyfloat: 調和関数の空間周波数。ピクセル単位で指定します。
thetafloat、オプション: ラジアン単位の方向。0 の場合、調和関数は x 方向にあります。
bandwidthfloat、オプション: フィルタによって捉えられる帯域幅。帯域幅が固定されている場合、sigma_x と sigma_y は周波数の増加とともに減少します。この値は、sigma_x と sigma_y がユーザーによって設定されている場合は無視されます。
sigma_x, sigma_yfloat、オプション: x 方向と y 方向の標準偏差。これらの方向は、回転 *前* のカーネルに適用されます。theta = pi/2 の場合、カーネルは 90 度回転するため、sigma_x は *垂直* 方向を制御します。
n_stdsスカラー、オプション: カーネルの線形サイズは、n_stds (デフォルトは 3) 標準偏差です。
offsetfloat、オプション: ラジアン単位の調和関数の位相オフセット。
dtype{np.complex64, np.complex128}: フィルタが単精度または倍精度の複素数であるかどうかを指定します。

戻り値：

g複素数配列: 複素フィルタカーネル。

参考文献

[1]

https://en.wikipedia.org/wiki/Gabor_filter

[2]

https://web.archive.org/web/20180127125930/http://mplab.ucsd.edu/tutorials/gabor.pdf

例

>>> from skimage.filters import gabor_kernel
>>> from matplotlib import pyplot as plt  

>>> gk = gabor_kernel(frequency=0.2)
>>> fig, ax = plt.subplots()  
>>> ax.imshow(gk.real)        
>>> plt.show()                

>>> # more ripples (equivalent to increasing the size of the
>>> # Gaussian spread)
>>> gk = gabor_kernel(frequency=0.2, bandwidth=0.1)
>>> fig, ax = plt.suplots()  
>>> ax.imshow(gk.real)       
>>> plt.show()               

テクスチャ分類のためのガボールフィルタバンク

skimage.filters.gaussian(image, sigma=1, *, mode='nearest', cval=0, preserve_range=False, truncate=4.0, channel_axis=None, out=None)[source]#

多次元ガウスフィルタ。

パラメータ：

imagendarray

フィルタリングする入力画像（グレースケールまたはカラー）。

sigmaスカラーまたはスカラーのシーケンス、オプション

ガウスカーネルの標準偏差。ガウスフィルタの標準偏差は、シーケンスとして各軸に与えられるか、単一の数字として与えられます。後者の場合、すべての軸で等しくなります。

mode{'reflect', 'constant', 'nearest', 'mirror', 'wrap'}、オプション

modeパラメータは、配列の境界の処理方法を決定します。ここで、cvalは、modeが'constant'の場合の値です。デフォルトは'nearest'です。

cvalスカラー、オプション

modeが'constant'の場合、入力の端を超えて埋め込む値。デフォルトは0.0です。

preserve_rangebool、オプション

True の場合、元の値の範囲を保持します。それ以外の場合は、入力 image は img_as_float の規則に従って変換されます（入力のデータ型に応じて、最初に [-1.0; 1.0] または [0; 1.0] の値に正規化されます）。

詳細については、以下を参照してください。 https://scikit-image.dokyumento.jp/docs/dev/user_guide/data_types.html

truncatefloat、オプション

この標準偏差の倍数でフィルタを打ち切ります。

channel_axisintまたはNone、オプション

Noneの場合、画像はグレースケール（シングルチャンネル）画像と見なされます。それ以外の場合は、このパラメータは、配列のどの軸がチャネルに対応するかを示します。

バージョン 0.19 で追加: channel_axis は 0.19 で追加されました。

outndarray、オプション

指定された場合、フィルタリングされた画像は、この配列に格納されます。

バージョン 0.23 で追加: out は 0.23 で追加されました。

戻り値：

filtered_imagendarray: フィルタリングされた配列。

注記

この関数は、scipy.ndimage.gaussian_filter() のラッパー関数です。

整数配列は浮動小数点数に変換されます。

gaussian は入力 image を浮動小数点数に変換するため、out は浮動小数点型のデータ型である必要があります。out が提供されない場合、別の配列が割り当てられ、結果として返されます。

多次元フィルタは、一連の1次元畳み込みフィルタとして実装されます。中間配列は、出力と同じデータ型で格納されます。したがって、精度が限られた出力型の場合、中間結果が不十分な精度で格納されるため、結果が不正確になる可能性があります。

例

>>> import skimage as ski
>>> a = np.zeros((3, 3))
>>> a[1, 1] = 1
>>> a
array([[0., 0., 0.],
       [0., 1., 0.],
       [0., 0., 0.]])
>>> ski.filters.gaussian(a, sigma=0.4)  # mild smoothing
array([[0.00163116, 0.03712502, 0.00163116],
       [0.03712502, 0.84496158, 0.03712502],
       [0.00163116, 0.03712502, 0.00163116]])
>>> ski.filters.gaussian(a, sigma=1)  # more smoothing
array([[0.05855018, 0.09653293, 0.05855018],
       [0.09653293, 0.15915589, 0.09653293],
       [0.05855018, 0.09653293, 0.05855018]])
>>> # Several modes are possible for handling boundaries
>>> ski.filters.gaussian(a, sigma=1, mode='reflect')
array([[0.08767308, 0.12075024, 0.08767308],
       [0.12075024, 0.16630671, 0.12075024],
       [0.08767308, 0.12075024, 0.08767308]])
>>> # For RGB images, each is filtered separately
>>> image = ski.data.astronaut()
>>> filtered_img = ski.filters.gaussian(image, sigma=1, channel_axis=-1)

skimage.filters.hessian(image, sigmas=range(1, 10, 2), scale_range=None, scale_step=None, alpha=0.5, beta=0.5, gamma=15, black_ridges=True, mode='reflect', cval=0)[ソース]#

ハイブリッドヘシアンフィルタで画像をフィルタリングします。

このフィルタは、血管、しわ、川など、連続的なエッジを検出するために使用できます。このようなオブジェクトを含む画像全体の割合を計算するためにも使用できます。

2次元および3次元画像のみに定義されています。Frangiフィルタとほぼ同等ですが、平滑化に代替の方法を使用しています。FrangiフィルタとHessianフィルタの違いについては、[1]を参照してください。

パラメータ：

image(M, N[, P]) ndarray: 入力画像データを含む配列。
sigmasfloat のイテラブル、オプション: フィルタのスケールとして使用されるシグマ値 (例: np.arange(scale_range[0], scale_range[1], scale_step))
scale_rangefloat の 2 要素タプル、オプション: 使用されるシグマ値の範囲。
scale_stepfloat、オプション: シグマ値の間隔。
betafloat、オプション: ブロブ状構造からのずれに対するフィルタの感度を調整する Frangi 補正定数。
gammafloat、オプション: フィルタの高分散/テクスチャ/構造の領域に対する感度を調整するFrangi補正定数。
black_ridgesboolean、オプション: True の場合 (デフォルト)、黒色の隆線を検出します。False の場合、白色の隆線を検出します。
mode{'constant', 'reflect', 'wrap', 'nearest', 'mirror'}、オプション: 画像境界外の値の処理方法。
cval浮動小数点数、オプション: mode 'constant' と共に使用される、画像境界外の値。

戻り値：

out(M, N[, P]) ndarray: フィルタリングされた画像 (すべてのスケールにわたるピクセルの最大値)。

こちらも参照してください

meijering
sato
frangi

注記

Marc Schrijverによる記述（2001年11月）Twente大学D. J. Kroonによる書き直し（2009年5月） [2]

参考文献

[1]

Ng, C. C., Yap, M. H., Costen, N., & Li, B. (2014,). ハイブリッドHessianフィルタを使用した自動しわ検出。アジアコンピュータビジョン会議（609-622ページ）。Springer International Publishing。DOI:10.1007/978-3-319-16811-1_40

[2]

Kroon, D. J.: Hessian based Frangi vesselness filter.

リッジ演算子

skimage.filters.laplace(image, ksize=3, mask=None)[ソース]#

ラプラス演算子を使用して画像のエッジを求めます。

パラメータ：

imagendarray: 処理対象の画像。
ksizeint、オプション: 離散ラプラシアン演算子のサイズを定義します。サイズは(ksize,) * image.ndimになります。
maskndarray、オプション: 適用範囲を特定の領域に制限するためのオプションマスク。マスク領域を囲むピクセルもマスクされ、マスク領域が結果に影響することを防ぎます。

戻り値：

outputndarray: ラプラシアンエッジマップ。

注記

ラプラシアン演算子は、skimage.restoration.uft.laplacian()関数を使用して生成されます。

skimage.filters.median(image, footprint=None, out=None, mode='nearest', cval=0.0, behavior='ndimage')[ソース]#

画像の局所中央値を返します。

パラメータ：

imagearray-like: 入力画像。
footprintndarray、オプション: behavior=='rank'の場合、footprintは1と0の2次元配列です。behavior=='ndimage'の場合、footprintはimageと同じ次元の1と0のN次元配列です。Noneの場合、footprintは各次元に対して3つの要素を持つN次元配列になります（例：ベクトル、正方形、立方体など）。
outndarray（imageと同じdtype）、オプション: Noneの場合、新しい配列が割り当てられます。
mode{'reflect', 'constant', 'nearest', 'mirror', 'wrap'}、オプション: modeパラメータは、配列の境界の処理方法を決定します。ここで、cvalはmodeが'constant'の場合の値です。デフォルトは'nearest'です。

バージョン0.15で追加: modeはbehavior='ndimage'で使用されます。
cvalスカラー、オプション: modeが'constant'の場合、入力の端を超えて埋める値。デフォルトは0.0です。

バージョン0.15で追加: cvalは0.15に追加され、behavior='ndimage'で使用されます。
behavior{'ndimage', 'rank'}、オプション: 古い動作（つまり、< 0.15）を使用するか、新しい動作を使用するかを指定します。古い動作はskimage.filters.rank.median()を呼び出します。新しい動作はscipy.ndimage.median_filter()を呼び出します。デフォルトは'ndimage'です。

バージョン0.15で追加: behaviorは0.15で導入されました。

バージョン0.16で変更: デフォルトのbehaviorは'rank'から'ndimage'に変更されました。

戻り値：

out2次元配列（入力画像と同じdtype）: 出力画像。

こちらも参照してください

skimage.filters.rank.median: 追加のパラメータでより柔軟性を提供する、メディアンフィルタリングのランクベースの実装ですが、符号なし整数画像専用です。

例

>>> from skimage import data
>>> from skimage.morphology import disk
>>> from skimage.filters import median
>>> img = data.camera()
>>> med = median(img, disk(5))

skimage.filters.meijering(image, sigmas=range(1, 10, 2), alpha=None, black_ridges=True, mode='reflect', cval=0)[ソース]#

Meijeringニューリティネスフィルタで画像をフィルタリングします。

このフィルタは、ニューライト、しわ、川など、連続的な尾根を検出するために使用できます。このようなオブジェクトを含む画像全体の割合を計算するためにも使用できます。

[1]で説明されている方法に従って、ヘッシアンの固有値を計算して、画像領域のニューライトとの類似度を計算します。

パラメータ：

image(M, N[, …]) ndarray: 入力画像データを含む配列。
sigmasfloat のイテラブル、オプション: フィルタのスケールとして使用されるシグマ
alphafloat、オプション: 最大限に平坦な細長い特徴を選択する整形フィルタ定数。デフォルトのNoneは、最適値-1/(ndim+1)を選択します。
black_ridgesboolean、オプション: True の場合 (デフォルト)、黒色の隆線を検出します。False の場合、白色の隆線を検出します。
mode{'constant', 'reflect', 'wrap', 'nearest', 'mirror'}、オプション: 画像境界外の値の処理方法。
cval浮動小数点数、オプション: mode 'constant' と共に使用される、画像境界外の値。

戻り値：

out(M, N[, …]) ndarray: フィルタリングされた画像 (すべてのスケールにわたるピクセルの最大値)。

こちらも参照してください

sato
frangi
hessian

参考文献

[1]

Meijering, E., Jacob, M., Sarria, J. C., Steiner, P., Hirling, H., Unser, M. (2004). 蛍光顕微鏡画像におけるニューライトのトレーシングと解析ツールの設計と検証。サイトメトリーパートA、58(2)、167-176。DOI:10.1002/cyto.a.20022

リッジ演算子

skimage.filters.prewitt(image, mask=None, *, axis=None, mode='reflect', cval=0.0)[ソース]#

Prewitt変換を使用してエッジの大きさを求めます。

パラメータ：

image配列

入力画像。

maskbool値の配列、オプション

出力画像をこのマスクにクリップします。(mask=0 の値は 0 に設定されます。)

axisint または int のシーケンス、オプション

この軸に沿ってエッジフィルタを計算します。指定しない場合、エッジの大きさが計算されます。これは次のように定義されます。

prw_mag = np.sqrt(sum([prewitt(image, axis=i)**2
                       for i in range(image.ndim)]) / image.ndim)

axis がシーケンスの場合も、大きさが計算されます。

mode文字列または文字列のシーケンス、オプション

畳み込みの境界モード。scipy.ndimage.convolve を参照して、モードの説明を確認してください。これは、単一の境界モード、または軸ごとの境界モードのいずれかです。

cval浮動小数点数、オプション

mode が 'constant' の場合、これは画像データの境界外の値に使用される定数です。

戻り値：

output浮動小数点数の配列: プレウィットエッジマップ。

こちらも参照してください

prewitt_h、prewitt_v: 水平および垂直エッジ検出。
sobel、scharr、farid、skimage.feature.canny

注記

エッジの大きさは、エッジの方向によってわずかに異なります。これは、Prewitt演算子による勾配演算子の近似が完全に回転不変ではないためです。より良い回転不変性のために、Scharr演算子を使用する必要があります。Sobel演算子はPrewitt演算子よりも回転不変性が優れていますが、Scharr演算子よりも劣ります。

例

>>> from skimage import data
>>> from skimage import filters
>>> camera = data.camera()
>>> edges = filters.prewitt(camera)

エッジオペレータ

skimage.filters.prewitt_h(image, mask=None)[source]#

Prewitt変換を使用して画像の水平エッジを求めます。

パラメータ：

image2次元配列: 処理対象の画像。
mask2次元配列、オプション: 適用範囲を特定の領域に制限するためのオプションマスク。マスク領域を囲むピクセルもマスクされ、マスク領域が結果に影響することを防ぎます。

戻り値：

output2次元配列: プレウィットエッジマップ。

注記

次のカーネルを使用します。

 1/3   1/3   1/3
  0     0     0
-1/3  -1/3  -1/3

エッジオペレータ

skimage.filters.prewitt_v(image, mask=None)[source]#

Prewitt変換を使用して画像の垂直エッジを求めます。

パラメータ：

image2次元配列: 処理対象の画像。
mask2次元配列、オプション: 適用範囲を特定の領域に制限するためのオプションマスク。マスク領域を囲むピクセルもマスクされ、マスク領域が結果に影響することを防ぎます。

戻り値：

output2次元配列: プレウィットエッジマップ。

注記

次のカーネルを使用します。

1/3   0  -1/3
1/3   0  -1/3
1/3   0  -1/3

エッジオペレータ

skimage.filters.rank_order(image)[source]#

imageの一意な値の昇順におけるピクセル値のインデックス（ランク順値）である、同じ形状の画像を返します。

パラメータ：

imagendarray

戻り値：

labelsimage.shape の形状を持つ符号なし整数の ndarray: 各ピクセルがimageの対応するピクセルのランク順の値を持つ新しい配列。ピクセル値は0からn-1の間です。ここで、nはimage内の異なる一意の値の数です。この配列のdtypeはnp.min_scalar_type(image.size)によって決定されます。
original_values1次元 ndarray: imageの一意の元の値。これはimageと同じdtypeになります。

例

>>> a = np.array([[1, 4, 5], [4, 4, 1], [5, 1, 1]])
>>> a
array([[1, 4, 5],
       [4, 4, 1],
       [5, 1, 1]])
>>> rank_order(a)
(array([[0, 1, 2],
       [1, 1, 0],
       [2, 0, 0]], dtype=uint8), array([1, 4, 5]))
>>> b = np.array([-1., 2.5, 3.1, 2.5])
>>> rank_order(b)
(array([0, 1, 2, 1], dtype=uint8), array([-1. ,  2.5,  3.1]))

skimage.filters.roberts(image, mask=None)[source]#

Robertsのクロス演算子を使用してエッジの大きさを求めます。

パラメータ：

image2次元配列: 処理対象の画像。
mask2次元配列、オプション: 適用範囲を特定の領域に制限するためのオプションマスク。マスク領域を囲むピクセルもマスクされ、マスク領域が結果に影響することを防ぎます。

戻り値：

output2次元配列: Robertsのクロスエッジマップ。

こちらも参照してください

roberts_pos_diag、roberts_neg_diag: 対角線エッジ検出。
sobel、scharr、prewitt、skimage.feature.canny

例

>>> from skimage import data
>>> camera = data.camera()
>>> from skimage import filters
>>> edges = filters.roberts(camera)

エッジオペレータ

skimage.filters.roberts_neg_diag(image, mask=None)[source]#

Robertsのクロス演算子を使用して画像のクロスエッジを見つけます。

カーネルは入力画像に適用され、勾配成分の別々の測定値を1つの向きで生成します。

パラメータ：

image2次元配列: 処理対象の画像。
mask2次元配列、オプション: 適用範囲を特定の領域に制限するためのオプションマスク。マスク領域を囲むピクセルもマスクされ、マスク領域が結果に影響することを防ぎます。

戻り値：

output2次元配列: Robertsのエッジマップ。

注記

次のカーネルを使用します。

 0   1
-1   0

skimage.filters.roberts_pos_diag(image, mask=None)[source]#

Robertsのクロス演算子を使用して画像のクロスエッジを見つけます。

カーネルは入力画像に適用され、勾配成分の別々の測定値を1つの向きで生成します。

パラメータ：

image2次元配列: 処理対象の画像。
mask2次元配列、オプション: 適用範囲を特定の領域に制限するためのオプションマスク。マスク領域を囲むピクセルもマスクされ、マスク領域が結果に影響することを防ぎます。

戻り値：

output2次元配列: Robertsのエッジマップ。

注記

次のカーネルを使用します。

1   0
0  -1

skimage.filters.sato(image, sigmas=range(1, 10, 2), black_ridges=True, mode='reflect', cval=0)[source]#

Satoチューブネスフィルタで画像をフィルタリングします。

このフィルタは、連続した尾根（例：チューブ、しわ、川）を検出するために使用できます。このようなオブジェクトを含む画像全体の割合を計算するために使用できます。

2次元および3次元画像に対してのみ定義されています。[1]で説明されている方法に従って、ヘッセ行列の固有値を計算して、チューブへの画像領域の類似度を計算します。

パラメータ：

image(M, N[, P]) ndarray: 入力画像データを含む配列。
sigmasfloat のイテラブル、オプション: フィルタの尺度として使用されるシグマ。
black_ridgesboolean、オプション: True の場合 (デフォルト)、黒色の隆線を検出します。False の場合、白色の隆線を検出します。
mode{'constant', 'reflect', 'wrap', 'nearest', 'mirror'}、オプション: 画像境界外の値の処理方法。
cval浮動小数点数、オプション: mode 'constant' と共に使用される、画像境界外の値。

戻り値：

out(M, N[, P]) ndarray: フィルタリングされた画像 (すべてのスケールにわたるピクセルの最大値)。

こちらも参照してください

meijering
frangi
hessian

参考文献

[1]

Sato, Y., Nakajima, S., Shiraga, N., Atsumi, H., Yoshida, S., Koller, T., …, Kikinis, R. (1998). Three-dimensional multi-scale line filter for segmentation and visualization of curvilinear structures in medical images. Medical image analysis, 2(2), 143-168. DOI:10.1016/S1361-8415(98)80009-1

リッジ演算子

ピクセルグラフを使用してオブジェクトの測地線中心を見つける

skimage.filters.scharr(image, mask=None, *, axis=None, mode='reflect', cval=0.0)[source]#

Scharr変換を使用してエッジの大きさを求めます。

パラメータ：

image配列

入力画像。

maskbool値の配列、オプション

出力画像をこのマスクにクリップします。(mask=0 の値は 0 に設定されます。)

axisint または int のシーケンス、オプション

この軸に沿ってエッジフィルタを計算します。指定しない場合、エッジの大きさが計算されます。これは次のように定義されます。

sch_mag = np.sqrt(sum([scharr(image, axis=i)**2
                       for i in range(image.ndim)]) / image.ndim)

axis がシーケンスの場合も、大きさが計算されます。

mode文字列または文字列のシーケンス、オプション

畳み込みの境界モード。scipy.ndimage.convolve を参照して、モードの説明を確認してください。これは、単一の境界モード、または軸ごとの境界モードのいずれかです。

cval浮動小数点数、オプション

mode が 'constant' の場合、これは画像データの境界外の値に使用される定数です。

戻り値：

output浮動小数点数の配列: Scharrのエッジマップ。

こちらも参照してください

scharr_h、scharr_v: 水平および垂直エッジ検出。
sobel、prewitt、farid、skimage.feature.canny

注記

Scharr演算子は、Sobel演算子やPrewitt演算子などの他のエッジフィルタよりも回転不変性に優れています。

参考文献

[1]

D. Kroon, 2009, Short Paper University Twente, Numerical Optimization of Kernel Based Image Derivatives。

[2]

https://en.wikipedia.org/wiki/Sobel_operator#Alternative_operators

例

>>> from skimage import data
>>> from skimage import filters
>>> camera = data.camera()
>>> edges = filters.scharr(camera)

エッジオペレータ

skimage.filters.scharr_h(image, mask=None)[source]#

Scharr変換を使用して画像の水平エッジを求めます。

パラメータ：

image2次元配列: 処理対象の画像。
mask2次元配列、オプション: 適用範囲を特定の領域に制限するためのオプションマスク。マスク領域を囲むピクセルもマスクされ、マスク領域が結果に影響することを防ぎます。

戻り値：

output2次元配列: Scharrのエッジマップ。

注記

次のカーネルを使用します。

 3   10   3
 0    0   0
-3  -10  -3

参考文献

[1]

D. Kroon, 2009, Short Paper University Twente, Numerical Optimization of Kernel Based Image Derivatives。

エッジオペレータ

skimage.filters.scharr_v(image, mask=None)[source]#

Scharr変換を使用して画像の垂直エッジを求めます。

パラメータ：

image2次元配列: 処理する画像
mask2次元配列、オプション: 適用範囲を特定の領域に制限するためのオプションマスク。マスク領域を囲むピクセルもマスクされ、マスク領域が結果に影響することを防ぎます。

戻り値：

output2次元配列: Scharrのエッジマップ。

注記

次のカーネルを使用します。

 0   -3
 0  -10
 0   -3

参考文献

[1]

D. Kroon, 2009, Short Paper University Twente, Numerical Optimization of Kernel Based Image Derivatives。

エッジオペレータ

skimage.filters.sobel(image, mask=None, *, axis=None, mode='reflect', cval=0.0)[source]#

Sobelフィルタを使用して画像のエッジを求めます。

パラメータ：

image配列

入力画像。

maskbool値の配列、オプション

出力画像をこのマスクにクリップします。(mask=0 の値は 0 に設定されます。)

axisint または int のシーケンス、オプション

この軸に沿ってエッジフィルタを計算します。指定しない場合、エッジの大きさが計算されます。これは次のように定義されます。

sobel_mag = np.sqrt(sum([sobel(image, axis=i)**2
                         for i in range(image.ndim)]) / image.ndim)

axis がシーケンスの場合も、大きさが計算されます。

mode文字列または文字列のシーケンス、オプション

畳み込みの境界モード。scipy.ndimage.convolve を参照して、モードの説明を確認してください。これは、単一の境界モード、または軸ごとの境界モードのいずれかです。

cval浮動小数点数、オプション

mode が 'constant' の場合、これは画像データの境界外の値に使用される定数です。

戻り値：

output浮動小数点数の配列: ソベルエッジマップ。

こちらも参照してください

sobel_h、sobel_v: 水平および垂直エッジ検出。
scharr、prewitt、farid、skimage.feature.canny

参考文献

[1]

D. Kroon, 2009, Short Paper University Twente, Numerical Optimization of Kernel Based Image Derivatives。

[2]

https://en.wikipedia.org/wiki/Sobel_operator

例

>>> from skimage import data
>>> from skimage import filters
>>> camera = data.camera()
>>> edges = filters.sobel(camera)

グレースケールフィルタのRGB画像への適用

エッジオペレータ

ヒステリシス閾値処理

領域境界ベースの領域隣接グラフ（RAG）

コンパクトウォーターシェッドを用いた規則セグメントの検出

オーバーラップなしでのセグメンテーションラベルの拡張

セグメンテーションとスーパーピクセルアルゴリズムの比較

エッジベースと領域ベースのセグメンテーションの比較

skimage.filters.sobel_h(image, mask=None)[source]#

Sobel変換を使用して画像の水平エッジを求めます。

パラメータ：

image2次元配列: 処理対象の画像。
mask2次元配列、オプション: 適用範囲を特定の領域に制限するためのオプションマスク。マスク領域を囲むピクセルもマスクされ、マスク領域が結果に影響することを防ぎます。

戻り値：

output2次元配列: ソベルエッジマップ。

注記

次のカーネルを使用します。

 1   2   1
 0   0   0
-1  -2  -1

エッジオペレータ

skimage.filters.sobel_v(image, mask=None)[source]#

Sobel変換を使用して画像の垂直エッジを求めます。

パラメータ：

image2次元配列: 処理対象の画像。
mask2次元配列、オプション: 適用範囲を特定の領域に制限するためのオプションマスク。マスク領域を囲むピクセルもマスクされ、マスク領域が結果に影響することを防ぎます。

戻り値：

output2次元配列: ソベルエッジマップ。

注記

次のカーネルを使用します。

 0  -1
 0  -2
 0  -1

エッジオペレータ

skimage.filters.threshold_isodata(image=None, nbins=256, return_all=False, *, hist=None)[source]#

ISODATA法に基づいて閾値を返します。

ヒストグラムベースの閾値処理（Ridler-Calvard法またはインターミーンズとしても知られる）。返される閾値は、以下の等式を満たします。

threshold = (image[image <= threshold].mean() +
             image[image > threshold].mean()) / 2.0

つまり、返される閾値は、画像を2つのピクセルグループに分割する強度であり、閾値強度はこれらのグループの平均強度のちょうど中間です。

整数画像の場合、上記の等式は1以内となります。浮動小数点画像の場合、上記の等式はヒストグラムのビン幅以内となります。

imageまたはhistのいずれかを指定する必要があります。histが指定されている場合、画像の実際のヒストグラムは無視されます。

パラメータ：

image(M, N[, …]) ndarray: グレースケール入力画像。
nbinsint, optional: ヒストグラムを計算するために使用されるビンの数。整数配列の場合は無視されます。
return_allbool, optional: False（デフォルト）の場合、上記の等式を満たす最小の閾値のみを返します。Trueの場合、すべての有効な閾値を返します。
histarray、または2つの配列のタプル, optional: 閾値を決定するためのヒストグラムと、対応するビンの中心強度の配列。あるいは、ヒストグラムのみを渡すこともできます。

戻り値：

thresholdfloatまたはintまたはarray: 閾値。

参考文献

[1]

Ridler, TW & Calvard, S (1978), “Picture thresholding using an iterative selection method” IEEE Transactions on Systems, Man and Cybernetics 8: 630-632, DOI:10.1109/TSMC.1978.4310039

[2]

Sezgin M. and Sankur B. (2004) “Survey over Image Thresholding Techniques and Quantitative Performance Evaluation” Journal of Electronic Imaging, 13(1): 146-165, http://www.busim.ee.boun.edu.tr/~sankur/SankurFolder/Threshold_survey.pdf DOI:10.1117/1.1631315

[3]

ImageJ AutoThresholderコード、http://fiji.sc/wiki/index.php/Auto_Threshold

例

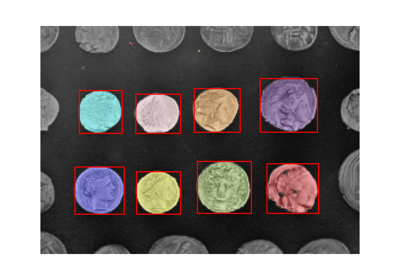
>>> from skimage.data import coins
>>> image = coins()
>>> thresh = threshold_isodata(image)
>>> binary = image > thresh

skimage.filters.threshold_li(image, *, tolerance=None, initial_guess=None, iter_callback=None)[source]#

Liの反復最小交差エントロピー法による閾値の計算。

パラメータ：

image(M, N[, …]) ndarray: グレースケール入力画像。
tolerancefloat, optional: 反復における閾値の変化がこの値を下回ったときに計算を終了します。デフォルトでは、これはimageの強度値間の最小差の半分です。
initial_guessfloatまたはCallable[[array[float]], float], optional: Liの反復方法は、最適な閾値を見つけるために勾配降下法を使用します。画像強度ヒストグラムが2つ以上のモード（ピーク）を持つ場合、勾配降下法は局所最適解に陥る可能性があります。反復の初期推定値は、アルゴリズムがグローバル最適な閾値を見つけるのに役立ちます。float値は特定の開始点を定義し、呼び出し可能オブジェクトは画像強度の配列を受け取り、float値を返す必要があります。numpy.mean（デフォルト）、lambda arr: numpy.quantile(arr, 0.95)、またはskimage.filters.threshold_otsu()などが有効な呼び出し可能オブジェクトの例です。
iter_callbackCallable[[float], Any], optional: アルゴリズムの各反復において閾値に対して呼び出される関数。

戻り値：

thresholdfloat: 上限閾値。この値より高い強度を持つすべてのピクセルは、前景と見なされます。

参考文献

[1]

Li C.H. and Lee C.K. (1993) “Minimum Cross Entropy Thresholding” Pattern Recognition, 26(4): 617-625 DOI:10.1016/0031-3203(93)90115-D

[2]

Li C.H. and Tam P.K.S. (1998) “An Iterative Algorithm for Minimum Cross Entropy Thresholding” Pattern Recognition Letters, 18(8): 771-776 DOI:10.1016/S0167-8655(98)00057-9

[3]

Sezgin M. and Sankur B. (2004) “Survey over Image Thresholding Techniques and Quantitative Performance Evaluation” Journal of Electronic Imaging, 13(1): 146-165 DOI:10.1117/1.1631315

[4]

ImageJ AutoThresholderコード、http://fiji.sc/wiki/index.php/Auto_Threshold

例

>>> from skimage.data import camera
>>> image = camera()
>>> thresh = threshold_li(image)
>>> binary = image > thresh

オブジェクトの除去

Li閾値処理

skimage.filters.threshold_local(image, block_size=3, method='gaussian', offset=0, mode='reflect', param=None, cval=0)[source]#

局所ピクセル近傍に基づいて閾値マスク画像を計算します。

適応閾値処理または動的閾値処理としても知られています。閾値は、ピクセルの局所近傍の加重平均から定数を引いたものです。あるいは、'generic'メソッドを使用して、指定された関数によって動的に閾値を決定することもできます。

パラメータ：

image(M, N[, …]) ndarray

グレースケール入力画像。

block_sizeintまたはintのシーケンス

閾値を計算するために使用されるピクセル近傍の奇数のサイズ（例：3、5、7、…、21、…）。

method{‘generic’, ‘gaussian’, ‘mean’, ‘median’}, optional

加重平均画像における局所近傍の適応閾値を決定するために使用される方法。

‘generic’：カスタム関数を使用（paramパラメータを参照）
‘gaussian’：ガウスフィルタを適用（カスタムシグマ値についてはparamパラメータを参照）
‘mean’：算術平均フィルタを適用
‘median’：中央値ランクフィルタを適用

デフォルトでは、'gaussian'メソッドが使用されます。

offsetfloat、オプション

局所閾値値を計算するために、近傍の加重平均から引かれる定数。デフォルトのオフセットは0です。

mode{'reflect', 'constant', 'nearest', 'mirror', 'wrap'}、オプション

modeパラメータは配列の境界の処理方法を決定し、modeが'constant'の場合、cvalはその値です。デフォルトは'reflect'です。

param{int, function}, optional

'gaussian'メソッドの場合はシグマを、'generic'メソッドの場合は関数オブジェクトを指定します。この関数は、局所近傍のフラットな配列を単一引数として受け取り、中心ピクセルの計算された閾値を返します。

cval浮動小数点数、オプション

モードが 'constant' の場合、入力の端を超えて埋め込む値。

戻り値：

threshold(M, N[, …]) ndarray: 閾値画像。入力画像内のすべてのピクセルで、閾値画像の対応するピクセルよりも高い値を持つピクセルは、前景とみなされます。

参考文献

[1]

Gonzalez, R. C. and Wood, R. E. “Digital Image Processing (2nd Edition).” Prentice-Hall Inc., 2002: 600–612. ISBN: 0-201-18075-8

例

>>> from skimage.data import camera
>>> image = camera()[:50, :50]
>>> binary_image1 = image > threshold_local(image, 15, 'mean')
>>> func = lambda arr: arr.mean()
>>> binary_image2 = image > threshold_local(image, 15, 'generic',
...                                         param=func)

インペインティングによる斑点のある角膜画像の修復

閾値処理

skimage.filters.threshold_mean(image)[source]#

グレースケール値の平均に基づいて閾値を返します。

パラメータ：

image(M, N[, …]) ndarray: グレースケール入力画像。

戻り値：

thresholdfloat: 上限閾値。この値より高い強度を持つすべてのピクセルは、前景と見なされます。

参考文献

[1]

C. A. Glasbey, “An analysis of histogram-based thresholding algorithms,” CVGIP: Graphical Models and Image Processing, vol. 55, pp. 532-537, 1993. DOI:10.1006/cgip.1993.1040

例

>>> from skimage.data import camera
>>> image = camera()
>>> thresh = threshold_mean(image)
>>> binary = image > thresh

閾値処理

skimage.filters.threshold_minimum(image=None, nbins=256, max_num_iter=10000, *, hist=None)[source]#

最小値法に基づいて閾値を返します。

指定されていない場合、入力 image のヒストグラムが計算され、最大値が2つになるまで平滑化されます。その後、その間の最小値が閾値となります。

imageまたはhistのいずれかを指定する必要があります。histが指定されている場合、画像の実際のヒストグラムは無視されます。

パラメータ：

image(M, N[, …]) ndarray, optional: グレースケール入力画像。
nbinsint, optional: ヒストグラムを計算するために使用されるビンの数。整数配列の場合は無視されます。
max_num_iterint, optional: ヒストグラムを平滑化する最大反復回数。
histarray、または2つの配列のタプル, optional: 閾値を決定するためのヒストグラムと、対応するビンの中心強度の配列。あるいは、ヒストグラムのみを渡すこともできます。

戻り値：

thresholdfloat: 上限閾値。この値より高い強度を持つすべてのピクセルは、前景と見なされます。

例外発生:

RuntimeError: ヒストグラム内で2つの局所的最大値が見つからない場合、または平滑化に1e4回を超える反復回数が必要な場合。

参考文献

[1]

C. A. Glasbey, “An analysis of histogram-based thresholding algorithms,” CVGIP: Graphical Models and Image Processing, vol. 55, pp. 532-537, 1993.

[2]

Prewitt, JMS & Mendelsohn, ML (1966), “The analysis of cell images”, Annals of the New York Academy of Sciences 128: 1035-1053 DOI:10.1111/j.1749-6632.1965.tb11715.x

例

>>> from skimage.data import camera
>>> image = camera()
>>> thresh = threshold_minimum(image)
>>> binary = image > thresh

閾値処理

金属合金の凝固の追跡

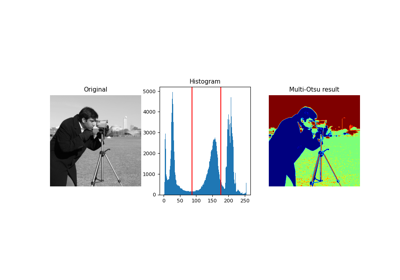
skimage.filters.threshold_multiotsu(image=None, classes=3, nbins=256, *, hist=None)[source]#

image内のグレースケールレベルを分割するためのclasses-1個の閾値を、複数クラスに対するOtsuの方法に従って生成します。

閾値は、閾値処理されたグレースケールクラス間のペアワイズ分散の合計を最大化するように選択されます。詳細については、注記と[1]を参照してください。

imageまたはhistのいずれかを指定する必要があります。histが指定されている場合、画像の実際のヒストグラムは無視されます。

パラメータ：

image(M, N[, …]) ndarray, optional: グレースケール入力画像。
classesint, optional: 閾値処理するクラスの数、つまり結果として得られる領域の数。
nbinsint, optional: ヒストグラムの計算に使用されるビンの数。整数配列の場合は、この値は無視されます。
histarray、または2つの配列のタプル, optional: 閾値を決定するためのヒストグラム、およびオプションで対応するビンの中心強度配列。histが指定されていない場合、この関数は画像からそれを計算します（注を参照）。

戻り値：

thresharray: 目的のクラスの閾値を含む配列。

例外発生:

ValueError: imageに、目的のクラス数よりも少ないグレースケール値が含まれている場合。

注記

この実装は、複雑さが\(O\left(\frac{Ch^{C-1}}{(C-1)!}\right)\)であるCython関数に依存しています。ここで\(h\)はヒストグラムビンの数、\(C\)は目的のクラス数です。

histが指定されていない場合、この関数はskimage.exposure.histogramを使用します。これはnp.histogramとは異なる動作をします。どちらも許容されますが、一貫した動作のために前者を使用してください。

入力画像はグレースケールである必要があります。

参考文献

[1]

Liao, P-S., Chen, T-S. and Chung, P-C., “A fast algorithm for multilevel thresholding”, Journal of Information Science and Engineering 17 (5): 713-727, 2001. Available at: <https://ftp.iis.sinica.edu.tw/JISE/2001/200109_01.pdf> DOI:10.6688/JISE.2001.17.5.1

[2]

Tosa, Y., “Multi-Otsu Threshold”, a java plugin for ImageJ. Available at: <http://imagej.net/plugins/download/Multi_OtsuThreshold.java>

例

>>> from skimage.color import label2rgb
>>> from skimage import data
>>> image = data.camera()
>>> thresholds = threshold_multiotsu(image)
>>> regions = np.digitize(image, bins=thresholds)
>>> regions_colorized = label2rgb(regions)

多クラスOtsu閾値処理

ピクセルグラフを使用してオブジェクトの測地線中心を見つける

ヒト細胞（分裂中）のセグメンテーション

skimage.filters.threshold_niblack(image, window_size=15, k=0.2)[source]#

配列にNiblack局所閾値を適用します。

次の式を使用して、画像内のすべてのピクセルに対して閾値Tが計算されます。

T = m(x,y) - k * s(x,y)

ここで、m(x,y)とs(x,y)は、ピクセルを中心としたサイズw×wの長方形のウィンドウによって定義されるピクセル(x,y)近傍の平均と標準偏差です。kは、標準偏差の影響を重み付ける構成可能なパラメータです。

パラメータ：

image(M, N[, …]) ndarray: グレースケール入力画像。
window_sizeint、またはintのiterable、optional: 単一の奇数整数（3、5、7…）として指定されたウィンドウサイズ、またはimage.ndimの長さのiterableで、奇数整数のみを含みます（例：(1, 5, 5)）。
kfloat, optional: 閾値式のパラメータkの値。

戻り値：

threshold(M, N[, …]) ndarray: 閾値マスク。この値より大きい強度を持つすべてのピクセルは、前景とみなされます。

注記

このアルゴリズムは、元々は文字認識のために設計されました。

Bradley閾値は、Niblack閾値の特別なケースであり、

>>> from skimage import data
>>> image = data.page()
>>> q = 1
>>> threshold_image = threshold_niblack(image, k=0) * q

ある値qに対して同等です。デフォルトでは、BradleyとRothはq=1を使用します。

参考文献

[1]

W. Niblack, An introduction to Digital Image Processing, Prentice-Hall, 1986.

[2]

D. Bradley and G. Roth, “Adaptive thresholding using Integral Image”, Journal of Graphics Tools 12(2), pp. 13-21, 2007. DOI:10.1080/2151237X.2007.10129236

例

>>> from skimage import data
>>> image = data.page()
>>> threshold_image = threshold_niblack(image, window_size=7, k=0.1)

NiblackとSauvola閾値処理

skimage.filters.threshold_otsu(image=None, nbins=256, *, hist=None)[source]#

Otsuの方法に基づいて閾値を返します。

imageまたはhistのいずれかを指定する必要があります。histが指定されている場合、画像の実際のヒストグラムは無視されます。

パラメータ：

image(M, N[, …]) ndarray, optional: グレースケール入力画像。
nbinsint, optional: ヒストグラムを計算するために使用されるビンの数。整数配列の場合は無視されます。
histarray、または2つの配列のタプル, optional: 閾値を決定するためのヒストグラム、およびオプションで対応するビンの中心強度配列。histが指定されていない場合、この関数は画像からそれを計算します。

戻り値：

thresholdfloat: 上限閾値。この値より高い強度を持つすべてのピクセルは、前景と見なされます。

注記

入力画像はグレースケールである必要があります。

参考文献

[1]

Wikipedia, https://en.wikipedia.org/wiki/Otsu’s_Method

例

>>> from skimage.data import camera
>>> image = camera()
>>> thresh = threshold_otsu(image)
>>> binary = image <= thresh

skimage.filters.threshold_sauvola(image, window_size=15, k=0.2, r=None)[source]#

Sauvola局所閾値を配列に適用します。SauvolaはNiblack手法の改良版です。

元の方法では、次の式を使用して画像内のすべてのピクセルに対して閾値Tが計算されます。

T = m(x,y) * (1 + k * ((s(x,y) / R) - 1))

ここで、m(x,y)とs(x,y)は、ピクセルを中心としたサイズw×wの長方形のウィンドウによって定義されるピクセル(x,y)近傍の平均と標準偏差です。kは、標準偏差の影響を重み付ける構成可能なパラメータです。Rはグレースケール画像の最大標準偏差です。

パラメータ：

image(M, N[, …]) ndarray: グレースケール入力画像。
window_sizeint、またはintのiterable、optional: 単一の奇数整数（3、5、7…）として指定されたウィンドウサイズ、またはimage.ndimの長さのiterableで、奇数整数のみを含みます（例：(1, 5, 5)）。
kfloat, optional: 正のパラメータkの値。
rfloat, optional: 標準偏差のダイナミックレンジRの値。Noneの場合、画像データ型の範囲の半分に設定されます。

戻り値：

threshold(M, N[, …]) ndarray: 閾値マスク。この値より大きい強度を持つすべてのピクセルは、前景とみなされます。

注記

このアルゴリズムは、元々は文字認識のために設計されました。

参考文献

[1]

J. Sauvola and M. Pietikainen, “Adaptive document image binarization,” Pattern Recognition 33(2), pp. 225-236, 2000. DOI:10.1016/S0031-3203(99)00055-2

例

>>> from skimage import data
>>> image = data.page()
>>> t_sauvola = threshold_sauvola(image, window_size=15, k=0.2)
>>> binary_image = image > t_sauvola

NiblackとSauvola閾値処理

skimage.filters.threshold_triangle(image, nbins=256)[source]#

三角アルゴリズムに基づいて閾値を返します。

パラメータ：

image(M, N[, …]) ndarray: グレースケール入力画像。
nbinsint, optional: ヒストグラムを計算するために使用されるビンの数。整数配列の場合は無視されます。

戻り値：

thresholdfloat: 上限閾値。この値より高い強度を持つすべてのピクセルは、前景と見なされます。

参考文献

[1]

Zack, G. W., Rogers, W. E. and Latt, S. A., 1977, Automatic Measurement of Sister Chromatid Exchange Frequency, Journal of Histochemistry and Cytochemistry 25 (7), pp. 741-753 DOI:10.1177/25.7.70454

[2]

ImageJ AutoThresholderコード、http://fiji.sc/wiki/index.php/Auto_Threshold

例

>>> from skimage.data import camera
>>> image = camera()
>>> thresh = threshold_triangle(image)
>>> binary = image > thresh

skimage.filters.threshold_yen(image=None, nbins=256, *, hist=None)[source]#

Yenの方法に基づいた閾値を返します。imageまたはhistのいずれかを指定する必要があります。histが指定された場合、画像の実際のヒストグラムは無視されます。

パラメータ：

image(M, N[, …]) ndarray: グレースケール入力画像。
nbinsint, optional: ヒストグラムを計算するために使用されるビンの数。整数配列の場合は無視されます。
histarray、または2つの配列のタプル, optional: 閾値を決定するためのヒストグラム、およびオプションで対応するビン中心強度配列。この関数の別の使用方法として、histのみを渡すこともできます。

戻り値：

thresholdfloat: 上限閾値。この値より高い強度を持つすべてのピクセルは、前景と見なされます。

参考文献

[1]

Yen J.C., Chang F.J., and Chang S. (1995) “A New Criterion for Automatic Multilevel Thresholding” IEEE Trans. on Image Processing, 4(3): 370-378. DOI:10.1109/83.366472

[2]

Sezgin M. and Sankur B. (2004) “Survey over Image Thresholding Techniques and Quantitative Performance Evaluation” Journal of Electronic Imaging, 13(1): 146-165, DOI:10.1117/1.1631315 http://www.busim.ee.boun.edu.tr/~sankur/SankurFolder/Threshold_survey.pdf

[3]

ImageJ AutoThresholderコード、http://fiji.sc/wiki/index.php/Auto_Threshold

例

>>> from skimage.data import camera
>>> image = camera()
>>> thresh = threshold_yen(image)
>>> binary = image <= thresh

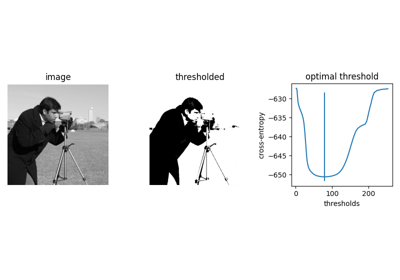
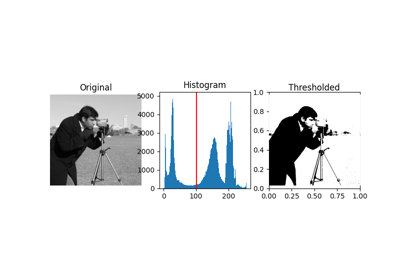
skimage.filters.try_all_threshold(image, figsize=(8, 5), verbose=True)[source]#

異なる閾値化方法の出力を比較する図を返します。

パラメータ：

image(M, N) ndarray: 入力画像。
figsizeタプル、オプション: 図のサイズ（インチ単位）。
verbose真偽値、オプション: 各メソッドの関数名を印刷します。

戻り値：

fig, axタプル: Matplotlibの図と軸。

注記

以下のアルゴリズムが使用されます。

isodata
li
mean
minimum
otsu
triangle
yen

例

>>> from skimage.data import text
>>> fig, ax = try_all_threshold(text(), figsize=(10, 6), verbose=False)

閾値処理

skimage.filters.unsharp_mask(image, radius=1.0, amount=1.0, preserve_range=False, *, channel_axis=None)[source]#

アンシャープマスキングフィルタ。

鮮明なディテールは、元の画像とそのぼかしバージョンとの違いとして識別されます。これらのディテールは、スケーリングされた後、元の画像に追加されます。

パラメータ：

image(M[, …][, C]) ndarray: 入力画像。
radiusスカラーまたはスカラーのシーケンス、オプション: スカラーが与えられた場合、その値はすべての次元で使用されます。シーケンスが与えられた場合、マルチチャネル画像の最後の次元を除く各次元に対して、正確に1つの半径が必要です。半径0はぼかしがないことを意味し、負の値は許可されません。
amountスカラー、オプション: ディテールはこの係数で増幅されます。係数は0または負になる可能性があります。通常、小さな正の数、たとえば1.0です。
preserve_rangebool、オプション: 元の値の範囲を維持するかどうか。そうでない場合、入力画像はimg_as_floatの規則に従って変換されます。https://scikit-image.dokyumento.jp/docs/dev/user_guide/data_types.htmlも参照してください。
channel_axisintまたはNone、オプション: Noneの場合、画像はグレースケール（シングルチャンネル）画像と見なされます。それ以外の場合は、このパラメータは、配列のどの軸がチャネルに対応するかを示します。

バージョン0.19で追加: channel_axisは0.19で追加されました。

戻り値：

output(M[, …][, C]) floatのndarray: アンシャープマスクが適用された画像。

注記

アンシャープマスクは画像強調技術です。これは線形画像演算であり、数値的に安定しています。これは、不適切な問題であるデコンボリューションとは異なります。この安定性のため、デコンボリューションよりも優先されることがよくあります。

主なアイデアは次のとおりです。鮮明なディテールは、元の画像とそのぼかしバージョンとの違いとして識別されます。これらのディテールは、スケーリングステップの後、元の画像に追加されます。

強調画像 = 元画像 + amount * (元画像 - ぼかし画像)

このフィルタを複数のカラーレイヤーに独立して適用すると、カラーブリーディングが発生する可能性があります。HSV、HSL、YUV、またはYCbCrなどの適切な色空間で明るさ/明度/強度チャネルのみを処理することで、より視覚的に優れた結果を得ることができます。

アンシャープマスクは、ほとんどの入門的なデジタル画像処理の本で説明されています。この実装は[1]に基づいています。

参考文献

[1]

Maria Petrou, Costas Petrou “Image Processing: The Fundamentals”, (2010), ed ii., page 357, ISBN 13: 9781119994398 DOI:10.1002/9781119994398

[2]

Wikipedia. アンシャープマスク https://en.wikipedia.org/wiki/Unsharp_masking

例

>>> array = np.ones(shape=(5,5), dtype=np.uint8)*100
>>> array[2,2] = 120
>>> array
array([[100, 100, 100, 100, 100],
       [100, 100, 100, 100, 100],
       [100, 100, 120, 100, 100],
       [100, 100, 100, 100, 100],
       [100, 100, 100, 100, 100]], dtype=uint8)
>>> np.around(unsharp_mask(array, radius=0.5, amount=2),2)
array([[0.39, 0.39, 0.39, 0.39, 0.39],
       [0.39, 0.39, 0.38, 0.39, 0.39],
       [0.39, 0.38, 0.53, 0.38, 0.39],
       [0.39, 0.39, 0.38, 0.39, 0.39],
       [0.39, 0.39, 0.39, 0.39, 0.39]])

>>> array = np.ones(shape=(5,5), dtype=np.int8)*100
>>> array[2,2] = 127
>>> np.around(unsharp_mask(array, radius=0.5, amount=2),2)
array([[0.79, 0.79, 0.79, 0.79, 0.79],
       [0.79, 0.78, 0.75, 0.78, 0.79],
       [0.79, 0.75, 1.  , 0.75, 0.79],
       [0.79, 0.78, 0.75, 0.78, 0.79],
       [0.79, 0.79, 0.79, 0.79, 0.79]])

>>> np.around(unsharp_mask(array, radius=0.5, amount=2, preserve_range=True), 2)
array([[100.  , 100.  ,  99.99, 100.  , 100.  ],
       [100.  ,  99.39,  95.48,  99.39, 100.  ],
       [ 99.99,  95.48, 147.59,  95.48,  99.99],
       [100.  ,  99.39,  95.48,  99.39, 100.  ],
       [100.  , 100.  ,  99.99, 100.  , 100.  ]])

アンシャープマスク

skimage.filters.wiener(data, impulse_response=None, filter_params=None, K=0.25, predefined_filter=None)[source]#

最小平均二乗誤差（ウィーナー）逆フィルタ。

パラメータ：

data(M, N) ndarray: 入力データ。
Kfloatまたは(M, N) ndarray: ノイズのパワースペクトルと劣化していない画像の比率。
impulse_response呼び出し可能 f(r, c, **filter_params): フィルタのインパルス応答。LPIFilter2D.__init__ を参照。
filter_params辞書、オプション: impulse_response 関数に追加のキーワードパラメータ。

その他のオプションパラメータ：

predefined_filterLPIFilter2D: 同じフィルタを異なる画像に対して複数回適用する必要がある場合、LPIFilter2D を構築し、ここで指定します。

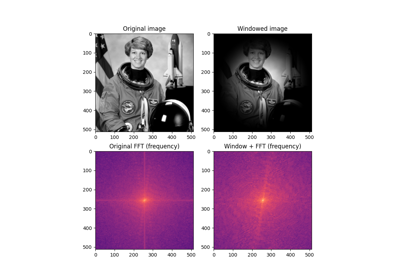
skimage.filters.window(window_type, shape, warp_kwargs=None)[source]#

指定されたサイズと次元数のn次元ウィンドウを返します。

パラメータ：

window_type文字列、浮動小数点数、またはタプル: scipy.signal.get_windowでサポートされているウィンドウタイプはすべてここに使用できます。現在のリストについては以下の注記、または使用しているSciPyのバージョンのSciPyドキュメントを参照してください。
shapeintのタプルまたはint: 各軸に沿ったウィンドウの形状。整数を与えると、1Dウィンドウが生成されます。
warp_kwargs辞書: skimage.transform.warpに渡されるキーワード引数（例：warp_kwargs={'order':3}で補間方法を変更）。

戻り値：

nd_windowndarray: 指定されたshapeのウィンドウ。dtypeはnp.float64です。

注記

この関数はscipy.signal.get_windowに基づいており、その関数で使用可能なすべてのウィンドウタイプ（例：「hann」、「boxcar」）にアクセスできます。特定のウィンドウタイプには、ウィンドウ名をタプルとしてパラメータを指定する必要があることに注意してください（例：「("tukey", 0.8)」）。浮動小数点数のみが指定されている場合、それはカイザーウィンドウのベータパラメータとして解釈されます。

詳細についてはhttps://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.windows.get_window.htmlを参照してください。

この関数は、指定されたshapeの倍精度配列を生成するため、使用可能なメモリを大量に消費する非常に大きな配列を生成する可能性があります。

ここでnDウィンドウを作成するために採用されたアプローチは、最初に目的のnDウィンドウの中心から配列内の各位置までのユークリッド距離を計算することです。scipy.signal.get_windowから返された1Dウィンドウから、その距離を使用して補間でサンプリングします。補間方法は、skimage.transform.warpに渡されるorderキーワード引数で変更できます。

出力ウィンドウの座標の一部は元の信号の外側にあります。これらは0で埋められます。

ウィンドウタイプ：- boxcar - triang - blackman - hamming - hann - bartlett - flattop - parzen - bohman - blackmanharris - nuttall - barthann - kaiser（ベータが必要）- gaussian（標準偏差が必要）- general_gaussian（パワー、幅が必要）- slepian（幅が必要）- dpss（正規化された半帯域幅が必要）- chebwin（減衰が必要）- exponential（減衰スケールが必要）- tukey（テーパ比が必要）

参考文献

[1]

2次元ウィンドウ設計、Wikipedia、https://en.wikipedia.org/wiki/Two_dimensional_window_design

例

形状(512, 512)のハニングウィンドウを返します。

>>> from skimage.filters import window
>>> w = window('hann', (512, 512))

ベータパラメータが16で、形状が(256, 256, 35)のカイザーウィンドウを返します。

>>> w = window(16, (256, 256, 35))

アルファパラメータが0.8で、形状が(100, 300)のチューキーウィンドウを返します。

>>> w = window(('tukey', 0.8), (100, 300))

登録のための極座標変換と対数極座標変換の使用

画像でのウィンドウ関数の使用

ガウシアン差分によるバンドパスフィルタリング

class skimage.filters.LPIFilter2D(impulse_response, **filter_params)[source]#

基本クラス：object

線形位置不変フィルタ（2次元）

__init__(impulse_response, **filter_params)[source]#

パラメータ：

impulse_response呼び出し可能 f(r, c, **filter_params)

インパルス応答を生成する関数。 r と c は、行と列の位置を表す1次元ベクトルです。つまり、座標は(r[0],c[0])、(r[0],c[1])などとなります。**filter_params はそのまま渡されます。

言い換えると、impulse_response は次のように呼び出されます。

>>> def impulse_response(r, c, **filter_params):
...     pass
>>>
>>> r = [0,0,0,1,1,1,2,2,2]
>>> c = [0,1,2,0,1,2,0,1,2]
>>> filter_params = {'kw1': 1, 'kw2': 2, 'kw3': 3}
>>> impulse_response(r, c, **filter_params)

例

係数の正規化を行わないガウシアンフィルタ

>>> def filt_func(r, c, sigma=1):
...     return np.exp(-(r**2 + c**2)/(2 * sigma**2))
>>> filter = LPIFilter2D(filt_func)

skimage.filters#

`skimage.filters`#