`skimage.graph`#

グラフベースの操作（例：最短経路）。

これには、画像内のピクセルの隣接グラフの作成、画像の中心ピクセルの検索、ピクセル間の（最小コスト）経路の検索、グラフのマージとカットなどがあります。

`central_pixel`	近接中心性（Closeness Centrality）が最も高いピクセルを見つける。
`cut_normalized`	領域隣接グラフ（RAG）に対して正規化されたグラフカットを実行する。
`cut_threshold`	閾値未満の重みで分離された領域を結合する。
`merge_hierarchical`	RAGの階層的マージを実行する。
`pixel_graph`	画像内のピクセルの隣接グラフを作成する。
`rag_boundary`	領域境界に基づいてRAGを計算する
`rag_mean_color`	平均色を使用して領域隣接グラフを計算する。
`route_through_array`	MCPおよびMCP_Geometricクラスの使用方法を示す簡単な例。
`shortest_path`	n次元配列内の一方から他方への最短経路を見つける。
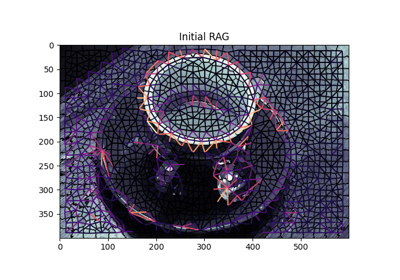
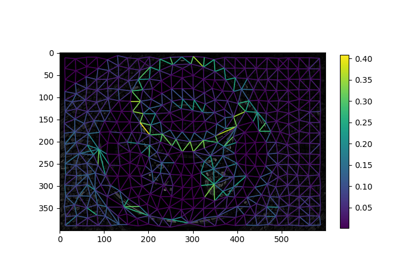
`show_rag`	画像上に領域隣接グラフを表示する。
`MCP`	与えられたn次元コスト配列を通る最小コスト経路を見つけるためのクラス。
`MCP_Connect`	距離加重最小コスト関数を使用してソースポイントを接続する。
`MCP_Flexible`	N次元コスト配列を通る最小コスト経路を見つける。
`MCP_Geometric`	n次元コスト配列を通る距離加重最小コスト経路を見つける。
`RAG`	画像の領域隣接グラフ（RAG）。`networkx.Graph`をサブクラス化。

skimage.graph.central_pixel(graph, nodes=None, shape=None, partition_size=100)[ソース]#

近接中心性（Closeness Centrality）が最も高いピクセルを見つける。

近接中心性とは、あるノードから他のすべてのノードへの最短距離の合計の逆数です。

パラメータ：

graphscipy.sparse.csr_array または scipy.sparse.csr_matrix: グラフの疎表現。
nodesintの配列: 画像内の各ノードのグラフにおけるラベリングされたインデックス。指定しない場合、返される値は入力グラフ内のインデックスになります。
shapeintのタプル: ノードが埋め込まれている画像の形状。指定した場合、返される座標は、入力形状と同じ次元のNumPy多次元インデックスになります。それ以外の場合は、nodesで提供されたラベリングされたインデックスが返されます。
partition_sizeint: この関数は、グラフ内のすべてのノードペア間の最短経路距離を計算します。これは非常に大きな（N*N）行列になる可能性があります。簡単なパフォーマンス調整として、距離値はpartition_sizeのロットで計算され、メモリ要件はpartition_size*Nのみになります。

戻り値：

positionintまたはintのタプル: shapeが指定されている場合、画像内の中心ピクセルの座標。そうでない場合、そのピクセルのラベリングされたインデックス。
distancesfloatの配列: 各ノードから到達可能な他の各ノードまでの距離の合計。

ピクセルグラフを使用してオブジェクトの測地中心を見つける

skimage.graph.cut_normalized(labels, rag, thresh=0.001, num_cuts=10, in_place=True, max_edge=1.0, *, rng=None)[ソース]#

領域隣接グラフ（RAG）に対して正規化されたグラフカットを実行する。

画像のラベルとその類似度RAGが与えられると、再帰的に2方向の正規化カットを実行します。さらにカットできないサブグラフに属するすべてのノードには、出力で一意のラベルが割り当てられます。

パラメータ：

labelsndarray

ラベルの配列。

ragRAG

領域隣接グラフ。

threshfloat

閾値。Nカットの値がthreshを超える場合、サブグラフはさらに細分されません。

num_cutsint

最適なものを決定する前に実行するNカットの数。

in_placebool

設定されている場合、ragをその場で変更します。各ノードnについて、関数はその新しい属性rag.nodes[n]['ncut label']を設定します。

max_edgefloat, optional

RAG内のエッジの最大値。これは、同一の領域間のエッジに対応します。これは、RAGに自己エッジを入れるために使用されます。

rng{numpy.random.Generator, int}, optional

擬似乱数ジェネレータ。デフォルトでは、PCG64ジェネレータが使用されます（numpy.random.default_rng()を参照）。rngがintの場合、ジェネレータのシードとして使用されます。

The rngはscipy.sparse.linalg.eigshの開始点を決定するために使用されます。

戻り値：

outndarray: 新しいラベル付き配列。

参考文献

[1]

Shi, J.; Malik, J., “Normalized cuts and image segmentation”, Pattern Analysis and Machine Intelligence, IEEE Transactions on, vol. 22, no. 8, pp. 888-905, August 2000.

例

>>> from skimage import data, segmentation, graph
>>> img = data.astronaut()
>>> labels = segmentation.slic(img)
>>> rag = graph.rag_mean_color(img, labels, mode='similarity')
>>> new_labels = graph.cut_normalized(labels, rag)

正規化カット

skimage.graph.cut_threshold(labels, rag, thresh, in_place=True)[ソース]#

閾値未満の重みで分離された領域を結合する。

画像のラベルとそのRAGが与えられると、指定された閾値未満の重みで接続されているノードを持つ領域を結合することで、新しいラベルを出力します。

パラメータ：

labelsndarray: ラベルの配列。
ragRAG: 領域隣接グラフ。
threshfloat: 閾値。より小さい重みのエッジで接続されている領域は結合されます。
in_placebool: 設定されている場合、rag をインプレースで変更します。この関数は、重みがthresh より小さいエッジを除去します。 False に設定されている場合、この関数は処理を開始する前にragのコピーを作成します。

戻り値：

outndarray: 新しいラベル付き配列。

参考文献

[1]

Alain Tremeau and Philippe Colantoni “Regions Adjacency Graph Applied To Color Image Segmentation” DOI:10.1109/83.841950

例

>>> from skimage import data, segmentation, graph
>>> img = data.astronaut()
>>> labels = segmentation.slic(img)
>>> rag = graph.rag_mean_color(img, labels)
>>> new_labels = graph.cut_threshold(labels, rag, 10)

領域隣接グラフ（RAG）の閾値処理

skimage.graph.merge_hierarchical(labels, rag, thresh, rag_copy, in_place_merge, merge_func, weight_func)[source]#

RAGの階層的マージを実行する。

thresh より低いエッジが残らないまで、最も類似したノードのペアを貪欲にマージします。

パラメータ：

labelsndarray: ラベルの配列。
ragRAG: 領域隣接グラフ。
threshfloat: 重みがthresh より小さいエッジで接続された領域はマージされます。
rag_copybool: 設定されている場合、変更する前にRAGがコピーされます。
in_place_mergebool: 設定されている場合、ノードはインプレースでマージされます。それ以外の場合は、マージごとに新しいノードが作成されます。
merge_funccallable: この関数は、2つのノードをマージする前に呼び出されます。RAG graph で src と dst をマージする際に、merge_func(graph, src, dst) のように呼び出されます。
weight_funccallable: マージされたノードに隣接するノードの新しい重みを計算する関数。これは、merge_nodes にweight_func 引数として直接渡されます。

戻り値：

outndarray: 新しいラベル付き配列。

領域隣接グラフ（RAG）のマージ

領域境界RAGの階層的マージ

skimage.graph.pixel_graph(image, *, mask=None, edge_function=None, connectivity=1, spacing=None, sparse_type='matrix')[source]#

画像内のピクセルの隣接グラフを作成する。

マスクがTrueであるピクセルは、返されるグラフのノードとなり、connectivityパラメータに従って隣接ピクセルにエッジで接続されます。デフォルトでは、マスクが与えられている場合、または画像自体がマスクである場合のエッジの値は、ピクセル間のユークリッド距離です。

ただし、マスクなしでint型またはfloat型の画像が与えられた場合、エッジの値は、隣接ピクセル間の強度差の絶対値に、ユークリッド距離を重み付けしたものです。

パラメータ：

imagearray: 入力画像。画像がbool型の場合、マスクとしても使用されます。
maskboolの配列: 使用するピクセル。Noneの場合、画像全体のグラフが使用されます。
edge_functioncallable: ピクセル値の配列、隣接ピクセル値の配列、距離の配列を受け取り、エッジの値を返す関数。関数が指定されていない場合、エッジの値は距離になります。
connectivityint: ピクセル近傍の正方接続性：ピクセルを隣接ピクセルとみなすために許容される直交ステップの数。scipy.ndimage.generate_binary_structureを参照してください。
spacingfloatのタプル: 各軸に沿ったピクセル間の間隔。
sparse_type{"matrix", "array"}, optional: graph の戻り値の型。 scipy.sparse.csr_array または scipy.sparse.csr_matrix（デフォルト）。

戻り値：

graphscipy.sparse.csr_matrix または scipy.sparse.csr_array: エントリ(i, j)が、ノードiとjが隣接している場合に1、そうでない場合に0である疎隣接行列。sparse_type によって、 scipy.sparse.csr_array として返される場合があります。
nodesintの配列: グラフのノード。これらは、マスク内のゼロ以外のピクセルのラベリングされたインデックスに対応します。

ピクセルグラフを使用してオブジェクトの測地中心を見つける

skimage.graph.rag_boundary(labels, edge_map, connectivity=2)[source]#

領域境界に基づいてRAGを計算する

画像の初期セグメンテーションとそのエッジマップが与えられると、このメソッドは対応する領域隣接グラフ（RAG）を構築します。RAG内の各ノードは、labels で同じラベルを持つ画像内のピクセルのセットを表します。隣接する2つの領域間の重みは、それらの境界に沿ったedge_map の平均値です。

labelsndarray: ラベル付けされた画像。
edge_mapndarray: これはlabels と同じ形状である必要があります。隣接する2つの領域間の境界に沿ったすべてのピクセルについて、edge_map の対応するピクセルの平均値が、それら間のエッジの重みになります。
connectivityint, optional: 互いからconnectivity 未満の2乗距離を持つピクセルは隣接しているとみなされます。1からlabels.ndim の範囲を取ります。その動作は、scipy.ndimage.generate_binary_structure のconnectivity パラメータと同じです。

例

>>> from skimage import data, segmentation, filters, color, graph
>>> img = data.chelsea()
>>> labels = segmentation.slic(img)
>>> edge_map = filters.sobel(color.rgb2gray(img))
>>> rag = graph.rag_boundary(labels, edge_map)

領域境界に基づく領域隣接グラフ（RAG）

領域境界RAGの階層的マージ

skimage.graph.rag_mean_color(image, labels, connectivity=2, mode='distance', sigma=255.0)[source]#

平均色を使用して領域隣接グラフを計算する。

このメソッドは、画像とその初期セグメンテーションが与えられると、対応する領域隣接グラフ（RAG）を構築します。RAG内の各ノードは、image内の同じラベルを持つピクセルの集合（labels内のラベル）を表します。隣接する2つの領域間の重みは、modeパラメータに応じて、2つの領域がどの程度似ているか、または異なっているかを表します。

パラメータ：

imagendarray, shape(M, N[, …, P], 3): 入力画像。
labelsndarray, shape(M, N[, …, P]): ラベル付けされた画像。これはimageよりも1次元少ない必要があります。imageの次元が(M, N, 3)の場合、labelsの次元は(M, N)である必要があります。
connectivityint, optional: 互いの二乗距離がconnectivity未満のピクセルは、隣接していると見なされます。これは1からlabels.ndimの範囲を取ります。その動作は、scipy.ndimage.generate_binary_structureのconnectivityパラメータと同じです。
mode{‘distance’, ‘similarity’}, optional: エッジ重みを割り当てるための戦略。

‘distance’ : 隣接する2つの領域間の重みは、\(|c_1 - c_2|\)です。ここで、\(c_1\)と\(c_2\)は2つの領域の平均色です。これは平均色におけるユークリッド距離を表します。

‘similarity’ : 隣接する2つの領域間の重みは、\(e^{-d^2/sigma}\)です。ここで、\(d=|c_1 - c_2|\)であり、\(c_1\)と\(c_2\)は2つの領域の平均色です。これは2つの領域がどの程度似ているかを表します。
sigmafloat, optional: modeが“similarity”の場合の計算に使用されます。これは、対応するエッジ重みが有意になるために、2つの色がどの程度近接しているべきかを制御します。sigmaの値が非常に大きいと、2つの色はいずれも似ているかのように振る舞う可能性があります。

戻り値：

outRAG: 領域隣接グラフ。

参考文献

[1]

Alain Tremeau and Philippe Colantoni “Regions Adjacency Graph Applied To Color Image Segmentation” DOI:10.1109/83.841950

例

>>> from skimage import data, segmentation, graph
>>> img = data.astronaut()
>>> labels = segmentation.slic(img)
>>> rag = graph.rag_mean_color(img, labels)

skimage.graph.route_through_array(array, start, end, fully_connected=True, geometric=True)[source]#

MCPおよびMCP_Geometricクラスの使用方法を示す簡単な例。

経路探索アルゴリズムの説明については、MCPクラスとMCP_Geometricクラスのドキュメントを参照してください。

パラメータ：

arrayndarray: コストの配列。
startiterable: arrayへのn次元インデックスで、始点を定義します。
enditerable: arrayへのn次元インデックスで、終点を定義します。
fully_connectedbool (optional): Trueの場合、対角移動が許可されます。Falseの場合、軸方向の移動のみが許可されます。
geometricbool (optional): Trueの場合、MCP_Geometricクラスを使用してコストが計算されます。Falseの場合、MCP基本クラスが使用されます。MCPとMCP_Geometricの違いについては、クラスのドキュメントを参照してください。

戻り値：

pathlist: startからendまでの経路を定義するn次元インデクスのタプルのリスト。
costfloat: 経路のコスト。geometricがFalseの場合、経路のコストは経路に沿ったarrayの値の合計です。geometricがTrueの場合、より詳細な計算が行われます（MCP_Geometricクラスのドキュメントを参照）。

参照

MCP, MCP_Geometric

例

>>> import numpy as np
>>> from skimage.graph import route_through_array
>>>
>>> image = np.array([[1, 3], [10, 12]])
>>> image
array([[ 1,  3],
       [10, 12]])
>>> # Forbid diagonal steps
>>> route_through_array(image, [0, 0], [1, 1], fully_connected=False)
([(0, 0), (0, 1), (1, 1)], 9.5)
>>> # Now allow diagonal steps: the path goes directly from start to end
>>> route_through_array(image, [0, 0], [1, 1])
([(0, 0), (1, 1)], 9.19238815542512)
>>> # Cost is the sum of array values along the path (16 = 1 + 3 + 12)
>>> route_through_array(image, [0, 0], [1, 1], fully_connected=False,
... geometric=False)
([(0, 0), (0, 1), (1, 1)], 16.0)
>>> # Larger array where we display the path that is selected
>>> image = np.arange((36)).reshape((6, 6))
>>> image
array([[ 0,  1,  2,  3,  4,  5],
       [ 6,  7,  8,  9, 10, 11],
       [12, 13, 14, 15, 16, 17],
       [18, 19, 20, 21, 22, 23],
       [24, 25, 26, 27, 28, 29],
       [30, 31, 32, 33, 34, 35]])
>>> # Find the path with lowest cost
>>> indices, weight = route_through_array(image, (0, 0), (5, 5))
>>> indices = np.stack(indices, axis=-1)
>>> path = np.zeros_like(image)
>>> path[indices[0], indices[1]] = 1
>>> path
array([[1, 1, 1, 1, 1, 0],
       [0, 0, 0, 0, 0, 1],
       [0, 0, 0, 0, 0, 1],
       [0, 0, 0, 0, 0, 1],
       [0, 0, 0, 0, 0, 1],
       [0, 0, 0, 0, 0, 1]])

skimage.graph.shortest_path(arr, reach=1, axis=-1, output_indexlist=False)[source]#

n次元配列内の一方から他方への最短経路を見つける。

パラメータ：

arrndarray of float64
reachint, optional: デフォルト(reach = 1)では、最短経路は、前方への移動ごとに最大で1行上または下に移動できます（つまり、経路の勾配は1に制限されます）。reachは、各ステップで各非軸次元をスキップできる要素数を定義します。
axisint, optional: 経路が常に前方へ移動しなければならない軸（デフォルト-1）。
output_indexlistbool, optional: 戻り値pの説明を参照してください。

戻り値：

piterable of int: axisに沿った各ステップについて、最短経路の座標。output_indexlistがTrueの場合、経路はarrにインデックス付けするn次元タプルのリストとして返されます。Falseの場合、経路は軸次元に沿った各ステップについて、非軸次元に沿った経路の座標をリストする配列として返されます。つまり、p.shape == (arr.shape[axis], arr.ndim-1)となりますが、返す前にpが圧縮されるため、arr.ndim == 2の場合、p.shape == (arr.shape[axis],)となります。
costfloat: 経路のコスト。これは、経路に沿ったすべての差の絶対値の合計です。

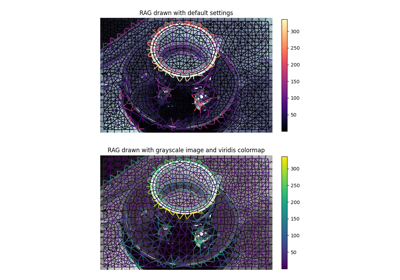
skimage.graph.show_rag(labels, rag, image, border_color='black', edge_width=1.5, edge_cmap='magma', img_cmap='bone', in_place=True, ax=None)[source]#

画像上に領域隣接グラフを表示する。

ラベル付けされた画像とその対応するRAGが与えられると、指定された色で画像上にRAGのノードとエッジを表示します。エッジは、画像内の2つの隣接領域の重心の間に表示されます。

パラメータ：

labelsndarray, shape (M, N): ラベル付けされた画像。
ragRAG: 領域隣接グラフ。
imagendarray, shape (M, N[, 3]): 入力画像。colormapがNoneの場合、画像はRGB形式である必要があります。
border_colorcolor spec, optional: 領域間の境界を描画する色。
edge_widthfloat, optional: RAGのエッジを描画する太さ。
edge_cmapmatplotlib.colors.Colormap, optional: エッジを描画するmatplotlibのカラマップ。
img_cmapmatplotlib.colors.Colormap, optional: 画像を描画するmatplotlibのカラマップ。Noneに設定すると、画像はそのまま描画されます。
in_placebool, optional: 設定されている場合、RAG はインプレースで変更されます。各ノードnに対して、この関数は新しい属性rag.nodes[n]['centroid']を設定します。
axmatplotlib.axes.Axes, optional: 描画するAxesオブジェクトです。指定されていない場合、新しいAxesオブジェクトが作成され、その上に描画されます。

戻り値：

lcmatplotlib.collections.LineCollection: グラフのエッジを表す線のコレクションです。matplotlib.figure.Figure.colorbar()関数に渡すことができます。

例

>>> from skimage import data, segmentation, graph
>>> import matplotlib.pyplot as plt
>>>
>>> img = data.coffee()
>>> labels = segmentation.slic(img)
>>> g =  graph.rag_mean_color(img, labels)
>>> lc = graph.show_rag(labels, g, img)
>>> cbar = plt.colorbar(lc)

領域境界に基づく領域隣接グラフ（RAG）

領域隣接グラフ（RAG）の描画

領域境界RAGの階層的マージ

class skimage.graph.MCP(costs, offsets=None, fully_connected=True, sampling=None)#

ベースクラス: object

与えられたn次元コスト配列を通る最小コスト経路を見つけるためのクラス。

n次元のコスト配列が与えられると、このクラスを使用して、任意の点の集合から別の任意の点の集合へのその配列を通る最小コストパスを見つけることができます。基本的な使い方は、クラスを初期化し、1つ以上の開始インデックス（およびオプションの終了インデックスのリスト）を使用してfind_costs()を呼び出すことです。その後、traceback()を1回以上呼び出して、任意の終了位置から最も近い開始インデックスへのパスを見つけます。同じコスト配列を通る新しいパスは、find_costs()を繰り返し呼び出すことで見つけることができます。

パスのコストは、パス上の各点におけるcosts配列の値の合計として単純に計算されます。一方、MCP_Geometricクラスは、対角線移動と軸方向移動の長さが異なるという事実を考慮し、パスコストをそれに応じて重み付けします。

無限大または負のコストを持つ配列要素は、累積コストが無限大にオーバーフローするパスと同様に、単に無視されます。

パラメータ：

costsndarray
offsetsiterable, optional: オフセットタプルのリストです。各オフセットは、与えられたn次元位置からの有効な移動を指定します。提供されない場合、fully_connectedパラメータ値を使用してmake_offsets()で構築された、単連結または完全連結n次元近傍に対応するオフセットが構築されます。
fully_connectedbool, optional: offsetsが提供されない場合、これは生成された近傍の連結性を決定します。Trueの場合、パスはcosts配列の要素間の対角線に沿って進むことができます。それ以外の場合は、軸方向の移動のみが許可されます。
samplingtuple, optional: 各次元について、2つのセル/ボクセル間の距離を指定します。指定されていない場合、またはNoneの場合、距離は単位距離と見なされます。

属性:

offsetsndarray: コンストラクタに提供されたoffsetsと等価です。提供されていない場合は、要求されたn次元近傍に対して作成されたオフセットです。これらは、find_costs()メソッドによって返されるtraceback配列を解釈するのに役立ちます。

__init__(costs, offsets=None, fully_connected=True, sampling=None)#: クラスのドキュメントを参照してください。

find_costs(starts, ends=None, find_all_ends=True, max_coverage=1.0, max_cumulative_cost=None, max_cost=None)#

指定された開始点から最小コストパスを見つけます。

このメソッドは、指定された開始インデックスのいずれかから、指定された終了インデックスへの最小コストパスを見つけます。終了位置が指定されていない場合、コスト配列内のすべての位置への最小コストパスが見つかります。

パラメータ：

startsiterable: n次元開始インデックスのリストです（ここでnはcosts配列の次元です）。最も近い/最も安価な開始点への最小コストパスが見つかります。
endsiterable, optional: n次元終了インデックスのリストです。
find_all_endsbool, optional: 「True」の場合（デフォルト）、指定されたすべての終了位置への最小コストパスが見つかります。それ以外の場合は、終了位置へのパスが見つかった時点でアルゴリズムが停止します。（endsが指定されていない場合、このパラメータは効果がありません。）

戻り値：

cumulative_costsndarray: costs配列と同じ形状です。この配列は、最も近い/最も安価な開始インデックスから、考慮された各インデックスまでの最小コストパスを記録します。（endsが指定されている場合、配列のすべての要素が必ずしも考慮されるわけではありません。評価されていない位置の累積コストはinfになります。find_all_endsが「False」の場合、指定された終了位置の1つのみが有限の累積コストを持ちます。）
tracebackndarray: costs配列と同じ形状です。この配列には、その先行インデックスからの任意のインデックスへのオフセットが含まれています。オフセットインデックスはoffsets属性をインデックス付けし、これはn次元オフセットの配列です。2次元の場合、offsets[traceback[x, y]]が(-1, -1)の場合、[x, y]の先行インデックスは、ある開始位置への最小コストパスにおける[x+1, y+1]であることを意味します。オフセットインデックスが-1の場合、そのインデックスは考慮されなかったことに注意してください。

goal_reached(index, cumcost)#

int goal_reached(int index, float cumcost) このメソッドは、ヒープからインデックスを取り出した後、各反復で、近傍を調べる前に呼び出されます。

このメソッドは、MCPアルゴリズムの動作を変更するためにオーバーロードできます。例としては、特定の累積コストに達した場合、またはフロントがシードポイントから特定の距離にある場合にアルゴリズムを停止させることが挙げられます。

このメソッドは、アルゴリズムが現在の点の近傍をチェックすべきでない場合は1を、アルゴリズムが完了した場合は2を返す必要があります。

offsets#

traceback(end)#

事前に計算されたtraceback配列を通じて最小コストパスをトレースします。

この便利な関数は、以前に呼び出された必要があるfind_costs()に提供された開始インデックスの1つから、特定の終了位置への最小コストパスを再構築します。この関数は、find_costs()が実行された後、必要な回数だけ呼び出すことができます。

パラメータ：

enditerable: costs配列へのn次元インデックスです。

戻り値：

tracebackn次元タプルのリスト: costs配列へのインデックスのリストで、find_costs()に渡された開始位置の1つから始まり、指定されたendインデックスで終わります。これらのインデックスは、任意の開始インデックスからendインデックスへの最小コストパスを指定します。（そのパスの総コストは、find_costs()によって返されるcumulative_costs配列から読み取ることができます。）

class skimage.graph.MCP_Connect(costs, offsets=None, fully_connected=True)#

基底クラス: MCP

距離加重最小コスト関数を使用してソースポイントを接続する。

各シードポイントから同時にフロントを成長させながら、フロントの起点も追跡します。2つのフロントが出会うと、create_connection()が呼び出されます。このメソッドは、アプリケーションに適した方法で検出されたエッジを処理するためにオーバーロードする必要があります。

__init__(*args, **kwargs)#

create_connection(id1, id2, tb1, tb2, cost1, cost2)#

create_connection id1, id2, pos1, pos2, cost1, cost2)

MCP処理中に検出された接続を追跡するために、このメソッドをオーバーロードします。同じIDを持つ接続は複数回検出される可能性があることに注意してください（ただし、位置とコストは異なります）。

このメソッドが呼び出された時点では、両方のポイントは「固定」されており、MCPアルゴリズムによって再度訪問されることはありません。

パラメータ：

id1int: 最初の隣接ノードの起点となったシードポイントのID。
id2int: 2番目の隣接ノードの起点となったシードポイントのID。
pos1タプル: 接続における最初の隣接ノードのインデックス。
pos2タプル: 接続における2番目の隣接ノードのインデックス。
cost1float: pos1における累積コスト。
cost2float: pos2における累積コスト。

find_costs(starts, ends=None, find_all_ends=True, max_coverage=1.0, max_cumulative_cost=None, max_cost=None)#

指定された開始点から最小コストパスを見つけます。

このメソッドは、指定された開始インデックスのいずれかから、指定された終了インデックスへの最小コストパスを見つけます。終了位置が指定されていない場合、コスト配列内のすべての位置への最小コストパスが見つかります。

パラメータ：

startsiterable: n次元開始インデックスのリストです（ここでnはcosts配列の次元です）。最も近い/最も安価な開始点への最小コストパスが見つかります。
endsiterable, optional: n次元終了インデックスのリストです。
find_all_endsbool, optional: 「True」の場合（デフォルト）、指定されたすべての終了位置への最小コストパスが見つかります。それ以外の場合は、終了位置へのパスが見つかった時点でアルゴリズムが停止します。（endsが指定されていない場合、このパラメータは効果がありません。）

戻り値：

cumulative_costsndarray: costs配列と同じ形状です。この配列は、最も近い/最も安価な開始インデックスから、考慮された各インデックスまでの最小コストパスを記録します。（endsが指定されている場合、配列のすべての要素が必ずしも考慮されるわけではありません。評価されていない位置の累積コストはinfになります。find_all_endsが「False」の場合、指定された終了位置の1つのみが有限の累積コストを持ちます。）
tracebackndarray: costs配列と同じ形状。この配列は、先行インデックスからの任意のインデックスへのオフセットを含みます。オフセットインデックスは、n次元オフセットの配列であるoffsets属性にインデックス付けされます。2次元の場合、offsets[traceback[x, y]]が(-1, -1)であるということは、ある開始位置への最小コストパスにおける[x, y]の先行ノードが[x+1, y+1]であることを意味します。オフセットインデックスが-1の場合、そのインデックスは考慮されなかったことに注意してください。

goal_reached(index, cumcost)#

int goal_reached(int index, float cumcost) このメソッドは、ヒープからインデックスを取り出した後、各反復で、近傍を調べる前に呼び出されます。

このメソッドは、MCPアルゴリズムの動作を変更するためにオーバーロードできます。例としては、特定の累積コストに達した場合、またはフロントがシードポイントから特定の距離にある場合にアルゴリズムを停止させることが挙げられます。

このメソッドは、アルゴリズムが現在の点の近傍をチェックすべきでない場合は1を、アルゴリズムが完了した場合は2を返す必要があります。

offsets#

traceback(end)#

事前に計算されたtraceback配列を通じて最小コストパスをトレースします。

この便利な関数は、以前に呼び出された必要があるfind_costs()に提供された開始インデックスの1つから、特定の終了位置への最小コストパスを再構築します。この関数は、find_costs()が実行された後、必要な回数だけ呼び出すことができます。

パラメータ：

enditerable: costs配列へのn次元インデックスです。

戻り値：

tracebackn次元タプルのリスト: costs配列へのインデックスのリストで、find_costs()に渡された開始位置の1つから始まり、指定されたendインデックスで終わります。これらのインデックスは、任意の開始インデックスからendインデックスへの最小コストパスを指定します。（そのパスの総コストは、find_costs()によって返されるcumulative_costs配列から読み取ることができます。）

class skimage.graph.MCP_Flexible(costs, offsets=None, fully_connected=True)#

基底クラス: MCP

N次元コスト配列を通る最小コスト経路を見つける。

詳細はMCPのドキュメントを参照してください。このクラスは、いくつかのメソッドを（純粋なPythonから）オーバーロードしてアルゴリズムの動作を変更したり、MCPに基づいてカスタムアルゴリズムを作成できるという点でMCPとは異なります。goal_reachedもMCPクラスでオーバーロードできることに注意してください。

__init__(costs, offsets=None, fully_connected=True, sampling=None)#: クラスのドキュメントを参照してください。

examine_neighbor(index, new_index, offset_length)#

このメソッドは、隣接するノードのペアごとに、両方のノードが固定されるとすぐに1回呼び出されます。

このメソッドは、隣接ノードに関する情報を取得したり、MCPアルゴリズムの動作を変更したりするためにオーバーロードできます。1つの例として、このフックを使用して、出会うフロントをチェックするMCP_Connectクラスがあります。

find_costs(starts, ends=None, find_all_ends=True, max_coverage=1.0, max_cumulative_cost=None, max_cost=None)#

指定された開始点から最小コストパスを見つけます。

このメソッドは、指定された開始インデックスのいずれかから、指定された終了インデックスへの最小コストパスを見つけます。終了位置が指定されていない場合、コスト配列内のすべての位置への最小コストパスが見つかります。

パラメータ：

startsiterable: n次元開始インデックスのリストです（ここでnはcosts配列の次元です）。最も近い/最も安価な開始点への最小コストパスが見つかります。
endsiterable, optional: n次元終了インデックスのリストです。
find_all_endsbool, optional: 「True」の場合（デフォルト）、指定されたすべての終了位置への最小コストパスが見つかります。それ以外の場合は、終了位置へのパスが見つかった時点でアルゴリズムが停止します。（endsが指定されていない場合、このパラメータは効果がありません。）

戻り値：

cumulative_costsndarray: costs配列と同じ形状です。この配列は、最も近い/最も安価な開始インデックスから、考慮された各インデックスまでの最小コストパスを記録します。（endsが指定されている場合、配列のすべての要素が必ずしも考慮されるわけではありません。評価されていない位置の累積コストはinfになります。find_all_endsが「False」の場合、指定された終了位置の1つのみが有限の累積コストを持ちます。）
tracebackndarray: costs配列と同じ形状。この配列は、先行インデックスからの任意のインデックスへのオフセットを含みます。オフセットインデックスは、n次元オフセットの配列であるoffsets属性にインデックス付けされます。2次元の場合、offsets[traceback[x, y]]が(-1, -1)であるということは、ある開始位置への最小コストパスにおける[x, y]の先行ノードが[x+1, y+1]であることを意味します。オフセットインデックスが-1の場合、そのインデックスは考慮されなかったことに注意してください。

goal_reached(index, cumcost)#

int goal_reached(int index, float cumcost) このメソッドは、ヒープからインデックスを取り出した後、各反復で、近傍を調べる前に呼び出されます。

このメソッドは、MCPアルゴリズムの動作を変更するためにオーバーロードできます。例としては、特定の累積コストに達した場合、またはフロントがシードポイントから特定の距離にある場合にアルゴリズムを停止させることが挙げられます。

このメソッドは、アルゴリズムが現在の点の近傍をチェックすべきでない場合は1を、アルゴリズムが完了した場合は2を返す必要があります。

offsets#

traceback(end)#

事前に計算されたtraceback配列を通じて最小コストパスをトレースします。

この便利な関数は、以前に呼び出された必要があるfind_costs()に提供された開始インデックスの1つから、特定の終了位置への最小コストパスを再構築します。この関数は、find_costs()が実行された後、必要な回数だけ呼び出すことができます。

パラメータ：

enditerable: costs配列へのn次元インデックスです。

戻り値：

tracebackn次元タプルのリスト: costs配列へのインデックスのリストで、find_costs()に渡された開始位置の1つから始まり、指定されたendインデックスで終わります。これらのインデックスは、任意の開始インデックスからendインデックスへの最小コストパスを指定します。（そのパスの総コストは、find_costs()によって返されるcumulative_costs配列から読み取ることができます。）

travel_cost(old_cost, new_cost, offset_length)#: このメソッドは、現在のノードから次のノードへの移動コストを計算します。デフォルトの実装はnew_costを返します。アルゴリズムの動作を適応させるために、このメソッドをオーバーロードします。

update_node(index, new_index, offset_length)#

このメソッドは、ノードが更新されたとき、new_indexがヒープにプッシュされ、トレースバックマップが更新された直後に呼び出されます。

このメソッドは、アルゴリズムの特定の実装で使用される他の配列を追跡するためにオーバーロードできます。たとえば、MCP_ConnectクラスはこれをIDマップの更新に使用します。

class skimage.graph.MCP_Geometric(costs, offsets=None, fully_connected=True)#

基底クラス: MCP

n次元コスト配列を通る距離加重最小コスト経路を見つける。

詳細はMCPのドキュメントを参照してください。このクラスは、パスのコストがそのパスに沿ったコストの単純な合計ではないという点でMCPとは異なります。

このクラスでは、costs配列の各位置に、その位置を通過する単位距離の「コスト」が含まれていると仮定します。例えば、(1, 1)から(1, 2)への移動（2次元）は、ピクセル(1, 1)の中心から(1, 2)の中心まで行われると仮定します。移動全体の長さは1で、その半分は(1, 1)を通過し、もう半分は(1, 2)を通過します。したがって、その移動のコストは(1/2)*costs[1,1] + (1/2)*costs[1,2]となります。

一方、(1, 1)から(2, 2)への移動は対角線上であり、長さはsqrt(2)です。この移動の半分はピクセル(1, 1)内であり、もう半分は(2, 2)内にあるため、この移動のコストは(sqrt(2)/2)*costs[1,1] + (sqrt(2)/2)*costs[2,2]として計算されます。

これらの計算は、1より大きい大きさのオフセットではあまり意味がありません。異方性データに対処するには、sampling引数を使用してください。

__init__(costs, offsets=None, fully_connected=True, sampling=None)#: クラスのドキュメントを参照してください。

find_costs(starts, ends=None, find_all_ends=True, max_coverage=1.0, max_cumulative_cost=None, max_cost=None)#

指定された開始点から最小コストパスを見つけます。

このメソッドは、指定された開始インデックスのいずれかから、指定された終了インデックスへの最小コストパスを見つけます。終了位置が指定されていない場合、コスト配列内のすべての位置への最小コストパスが見つかります。

パラメータ：

startsiterable: n次元開始インデックスのリストです（ここでnはcosts配列の次元です）。最も近い/最も安価な開始点への最小コストパスが見つかります。
endsiterable, optional: n次元終了インデックスのリストです。
find_all_endsbool, optional: 「True」の場合（デフォルト）、指定されたすべての終了位置への最小コストパスが見つかります。それ以外の場合は、終了位置へのパスが見つかった時点でアルゴリズムが停止します。（endsが指定されていない場合、このパラメータは効果がありません。）

戻り値：

cumulative_costsndarray: costs配列と同じ形状です。この配列は、最も近い/最も安価な開始インデックスから、考慮された各インデックスまでの最小コストパスを記録します。（endsが指定されている場合、配列のすべての要素が必ずしも考慮されるわけではありません。評価されていない位置の累積コストはinfになります。find_all_endsが「False」の場合、指定された終了位置の1つのみが有限の累積コストを持ちます。）
tracebackndarray: costs配列と同じ形状です。この配列には、先行インデックスからの任意のインデックスへのオフセットが含まれています。オフセットインデックスは、n次元オフセットの配列であるoffsets属性にインデックス付けします。2次元の場合、offsets[traceback[x, y]]が(-1, -1)である場合、最小コストパスにおける[x, y]の先行要素は[x+1, y+1]であることを意味します。offset_indexが-1の場合、そのインデックスは考慮されなかったことに注意してください。

goal_reached(index, cumcost)#

int goal_reached(int index, float cumcost) このメソッドは、ヒープからインデックスを取り出した後、各反復で、近傍を調べる前に呼び出されます。

このメソッドは、MCPアルゴリズムの動作を変更するためにオーバーロードできます。例としては、特定の累積コストに達した場合、またはフロントがシードポイントから特定の距離にある場合にアルゴリズムを停止させることが挙げられます。

このメソッドは、アルゴリズムが現在の点の近傍をチェックすべきでない場合は1を、アルゴリズムが完了した場合は2を返す必要があります。

offsets#

traceback(end)#

事前に計算されたtraceback配列を通じて最小コストパスをトレースします。

この便利な関数は、以前に呼び出された必要があるfind_costs()に提供された開始インデックスの1つから、特定の終了位置への最小コストパスを再構築します。この関数は、find_costs()が実行された後、必要な回数だけ呼び出すことができます。

パラメータ：

enditerable: costs配列へのn次元インデックスです。

戻り値：

tracebackn次元タプルのリスト: costs配列へのインデックスのリストで、find_costs()に渡された開始位置の1つから始まり、指定されたendインデックスで終わります。これらのインデックスは、任意の開始インデックスからendインデックスへの最小コストパスを指定します。（そのパスの総コストは、find_costs()によって返されるcumulative_costs配列から読み取ることができます。）

class skimage.graph.RAG(label_image=None, connectivity=1, data=None, **attr)[source]#

基底クラス: Graph

画像の領域隣接グラフ（RAG）。networkx.Graphをサブクラス化。

パラメータ：

label_image整数型配列: 初期セグメンテーション。各領域は異なる整数でラベル付けされます。label_image内の各一意の値は、グラフ内のノードに対応します。
connectivityint in {1, …, label_image.ndim}, optional: label_image内のピクセル間の接続性。2次元画像の場合、接続性1は上下左右の隣接ピクセルに対応し、接続性2は対角線上の隣接ピクセルも含みます。scipy.ndimage.generate_binary_structure()を参照してください。
datanetworkx.Graph specification, optional: networkx.Graphコンストラクタに渡す初期のエッジまたは追加のエッジ。有効なエッジの指定には、エッジリスト（タプルのリスト）、NumPy配列、SciPyスパース行列などがあります。
**attrキーワード引数, optional: グラフに追加する属性。

__init__(label_image=None, connectivity=1, data=None, **attr)[source]#

エッジ、名前、またはグラフ属性を持つグラフを初期化します。

パラメータ：

incoming_graph_data入力グラフ (optional, default: None): グラフを初期化するデータ。None（デフォルト）の場合、空のグラフが作成されます。データはエッジリスト、または任意のNetworkXグラフオブジェクトにすることができます。対応するオプションのPythonパッケージがインストールされている場合、データは2D NumPy配列、SciPyスパース配列、またはPyGraphvizグラフにすることもできます。
attrキーワード引数, optional (default= no attributes): key=valueのペアとしてグラフに追加する属性。

参照

変換

例

>>> G = nx.Graph()  # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G = nx.Graph(name="my graph")
>>> e = [(1, 2), (2, 3), (3, 4)]  # list of edges
>>> G = nx.Graph(e)

任意のグラフ属性ペア（key=value）を割り当てることができます。

>>> G = nx.Graph(e, day="Friday")
>>> G.graph
{'day': 'Friday'}

add_edge(u, v, attr_dict=None, **attr)[source]#: 最大ノードIDを更新しながら、uとvの間にエッジを追加します。

参照

networkx.Graph.add_edge.

add_edges_from(ebunch_to_add, **attr)[source]#

ebunch_to_add内のすべてのエッジを追加します。

パラメータ：

ebunch_to_addエッジのコンテナ: コンテナに与えられた各エッジはグラフに追加されます。エッジは2タプル(u, v)または3タプル(u, v, d)で指定する必要があります。ここで、dはエッジデータを含む辞書です。
attrキーワード引数, optional: キーワード引数を使用して、エッジデータ（またはラベルまたはオブジェクト）を割り当てることができます。

参照

add_edge: 単一のエッジを追加する
add_weighted_edges_from: 重み付きエッジを追加する便利な方法

注記

同じエッジを2回追加しても効果はありませんが、重複したエッジが追加されるたびにエッジデータは更新されます。

ebunchで指定されたエッジ属性は、キーワード引数で指定された属性よりも優先されます。

グラフを反復処理しながら変更しているグラフ上のイテレータからエッジを追加する場合、RuntimeErrorがメッセージ「RuntimeError: dictionary changed size during iteration」で発生する可能性があります。これは、反復処理中にグラフの基盤となる辞書が変更された場合に発生します。このエラーを回避するには、list(iterator_of_edges)を使用してイテレータを別のオブジェクトに評価し、そのオブジェクトをG.add_edges_fromに渡してください。

例

>>> G = nx.Graph()  # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_edges_from([(0, 1), (1, 2)])  # using a list of edge tuples
>>> e = zip(range(0, 3), range(1, 4))
>>> G.add_edges_from(e)  # Add the path graph 0-1-2-3

エッジにデータを関連付ける

>>> G.add_edges_from([(1, 2), (2, 3)], weight=3)
>>> G.add_edges_from([(3, 4), (1, 4)], label="WN2898")

同じグラフを変更するために使用している場合は、グラフ上のイテレータを評価する

>>> G = nx.Graph([(1, 2), (2, 3), (3, 4)])
>>> # Grow graph by one new node, adding edges to all existing nodes.
>>> # wrong way - will raise RuntimeError
>>> # G.add_edges_from(((5, n) for n in G.nodes))
>>> # correct way - note that there will be no self-edge for node 5
>>> G.add_edges_from(list((5, n) for n in G.nodes))

add_node(n, attr_dict=None, **attr)[source]#: 最大ノードIDを更新しながら、ノードnを追加します。

参照

networkx.Graph.add_node.

add_nodes_from(nodes_for_adding, **attr)[source]#

複数のノードを追加します。

パラメータ：

nodes_for_adding反復可能コンテナ: ノードのコンテナ（リスト、辞書、集合など）。または、(ノード、属性辞書)タプルのコンテナ。属性辞書を使用してノード属性を更新します。
attrキーワード引数, optional (default= no attributes): nodes内のすべてのノードの属性を更新します。タプルとしてnodesに指定されたノード属性は、キーワード引数で指定された属性よりも優先されます。

参照

add_node

注記

グラフを変更中にグラフ上のイテレータからノードを追加する場合、RuntimeErrorが「RuntimeError: dictionary changed size during iteration」というメッセージで発生する可能性があります。これは、イテレーション中にグラフの基礎となる辞書が変更された場合に発生します。list(iterator_of_nodes)を使用してイテレータを別個のオブジェクト（例：リスト）に評価し、そのオブジェクトをG.add_nodes_fromに渡すことで、このエラーを回避できます。

例

>>> G = nx.Graph()  # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_nodes_from("Hello")
>>> K3 = nx.Graph([(0, 1), (1, 2), (2, 0)])
>>> G.add_nodes_from(K3)
>>> sorted(G.nodes(), key=str)
[0, 1, 2, 'H', 'e', 'l', 'o']

キーワードを使用して、すべてのノードの特定のノード属性を更新します。

>>> G.add_nodes_from([1, 2], size=10)
>>> G.add_nodes_from([3, 4], weight=0.4)

(ノード、attrdict)タプルを使用して、特定のノードの属性を更新します。

>>> G.add_nodes_from([(1, dict(size=11)), (2, {"color": "blue"})])
>>> G.nodes[1]["size"]
11
>>> H = nx.Graph()
>>> H.add_nodes_from(G.nodes(data=True))
>>> H.nodes[1]["size"]
11

同じグラフを変更するために使用している場合は、グラフ上のイテレータを評価する

>>> G = nx.Graph([(0, 1), (1, 2), (3, 4)])
>>> # wrong way - will raise RuntimeError
>>> # G.add_nodes_from(n + 1 for n in G.nodes)
>>> # correct way
>>> G.add_nodes_from(list(n + 1 for n in G.nodes))

add_weighted_edges_from(ebunch_to_add, weight='weight', **attr)[source]#

ebunch_to_add内の重み付きエッジを指定されたweight属性で追加します。

パラメータ：

ebunch_to_addエッジのコンテナ: リストまたはコンテナに与えられた各エッジは、グラフに追加されます。エッジは、wが数値である3タプル(u, v, w)として指定する必要があります。
weight文字列、オプション（デフォルト='weight'): 追加するエッジの重みのための属性名。
attrキーワード引数, optional (default= no attributes): すべてのエッジに対して追加/更新するエッジ属性。

参照

add_edge: 単一のエッジを追加する
add_edges_from: 複数エッジを追加

注記

Graph/DiGraphに対して同じエッジを2回追加すると、エッジデータが単純に更新されます。MultiGraph/MultiDiGraphでは、重複したエッジが保存されます。

グラフを変更中にグラフ上のイテレータからエッジを追加する場合、RuntimeErrorが「RuntimeError: dictionary changed size during iteration」というメッセージで発生する可能性があります。これは、イテレーション中にグラフの基礎となる辞書が変更された場合に発生します。list(iterator_of_edges)を使用してイテレータを別個のオブジェクト（例：リスト）に評価し、そのオブジェクトをG.add_weighted_edges_fromに渡すことで、このエラーを回避できます。

例

>>> G = nx.Graph()  # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_weighted_edges_from([(0, 1, 3.0), (1, 2, 7.5)])

エッジのイテレータを渡す前に評価します。

>>> G = nx.Graph([(1, 2), (2, 3), (3, 4)])
>>> weight = 0.1
>>> # Grow graph by one new node, adding edges to all existing nodes.
>>> # wrong way - will raise RuntimeError
>>> # G.add_weighted_edges_from(((5, n, weight) for n in G.nodes))
>>> # correct way - note that there will be no self-edge for node 5
>>> G.add_weighted_edges_from(list((5, n, weight) for n in G.nodes))

property adj#

各ノードの隣接ノードを保持するグラフ隣接オブジェクト。

このオブジェクトは、ノードキーと隣接ノード辞書値を持つ読み取り専用の辞書のような構造です。隣接ノード辞書は、隣接ノードをエッジデータ辞書に関連付けます。そのため、G.adj[3][2]['color'] = 'blue'は、エッジ(3, 2)の色を"blue"に設定します。

G.adjの反復処理は辞書のように動作します。有用なイディオムにはfor nbr, datadict in G.adj[n].items():が含まれます。

隣接ノード情報は、グラフの添字アクセスによっても提供されます。そのため、for nbr, foovalue in G[node].data('foo', default=1):も機能します。

有向グラフの場合、G.adjは、発信（後続）情報を保持します。

adjacency()[source]#

すべてのノードについて、(ノード、隣接辞書)タプルのイテレータを返します。

有向グラフの場合、発信隣接ノードのみが含まれます。

戻り値：

adj_iterイテレータ: グラフ内のすべてのノードについて、(ノード、隣接辞書)のイテレータ。

例

>>> G = nx.path_graph(4)  # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> [(n, nbrdict) for n, nbrdict in G.adjacency()]
[(0, {1: {}}), (1, {0: {}, 2: {}}), (2, {1: {}, 3: {}}), (3, {2: {}})]

adjlist_inner_dict_factory#: dictのエイリアス

adjlist_outer_dict_factory#: dictのエイリアス

clear()[source]#

グラフからすべてのノードとエッジを削除します。

これにより、名前とすべてのグラフ、ノード、エッジ属性も削除されます。

例

>>> G = nx.path_graph(4)  # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.clear()
>>> list(G.nodes)
[]
>>> list(G.edges)
[]

clear_edges()[source]#

ノードを変更せずに、グラフからすべてのエッジを削除します。

例

>>> G = nx.path_graph(4)  # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.clear_edges()
>>> list(G.nodes)
[0, 1, 2, 3]
>>> list(G.edges)
[]

copy()[source]#: 最大ノードIDと共にグラフをコピーします。

参照

networkx.Graph.copy.

property degree#

G.degreeまたはG.degree()としてグラフのDegreeView。

ノード次数は、ノードに隣接するエッジの数です。重み付きノード次数は、そのノードに接続するエッジの重みの合計です。

このオブジェクトは、(ノード、次数)のイテレータと、単一ノードの次数のルックアップを提供します。

パラメータ：

nbunch単一ノード、コンテナ、またはすべてのノード（デフォルト=すべてのノード）: このビューは、これらのノードに接続するエッジのみを報告します。
weight文字列またはNone、オプション（デフォルト=None）: 重みとして使用される数値値を保持するエッジ属性の名前。Noneの場合、各エッジの重みは1です。次数は、ノードに隣接するエッジの重みの合計です。

戻り値：

DegreeViewまたはint: 複数のノードが要求された場合（デフォルト）、ノードとその次数をマッピングするDegreeViewを返します。単一のノードが要求された場合、ノードの次数を整数として返します。

例

>>> G = nx.path_graph(4)  # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.degree[0]  # node 0 has degree 1
1
>>> list(G.degree([0, 1, 2]))
[(0, 1), (1, 2), (2, 2)]

edge_attr_dict_factory#: dictのエイリアス

edge_subgraph(edges)[source]#

指定されたエッジによって誘導された部分グラフを返します。

誘導された部分グラフには、edges内の各エッジと、それらのエッジのいずれかに接続する各ノードが含まれます。

パラメータ：

edges反復可能オブジェクト: このグラフのエッジのイテレータ。

戻り値：

Gグラフ: 同じエッジ属性を持つ、このグラフのエッジ誘導部分グラフ。

注記

返される部分グラフビューのグラフ、エッジ、ノード属性は、元のグラフの対応する属性への参照です。ビューは読み取り専用です。

エッジまたはノード属性の独自の複製を持つ部分グラフの完全なグラフバージョンを作成するには、

G.edge_subgraph(edges).copy()

例

>>> G = nx.path_graph(5)
>>> H = G.edge_subgraph([(0, 1), (3, 4)])
>>> list(H.nodes)
[0, 1, 3, 4]
>>> list(H.edges)
[(0, 1), (3, 4)]

property edges#

G.edgesまたはG.edges()としてグラフのEdgeView。

edges(self, nbunch=None, data=False, default=None)

EdgeViewは、エッジタプルに対する集合のような操作とエッジ属性のルックアップを提供します。呼び出されたとき、エッジ属性へのアクセスを制御するEdgeDataViewオブジェクトも提供しますが（集合のような操作は提供しません）、G.edges[u, v]['color']はエッジ(u, v)の色属性の値を提供し、一方for (u, v, c) in G.edges.data('color', default='red'):は、色属性が存在しない場合はデフォルトの'red'を使用して、すべてエッジを反復処理して色属性を生成します。

パラメータ：

nbunch単一ノード、コンテナ、またはすべてのノード（デフォルト=すべてのノード）: このビューは、これらのノードからのエッジのみを報告します。
data文字列またはbool、オプション（デフォルト=False）: 3タプル(u, v, ddict[data])で返されるエッジ属性。Trueの場合、3タプル(u, v, ddict)でエッジ属性辞書を返します。Falseの場合、2タプル(u, v)を返します。
default値、オプション（デフォルト=None）: 要求された属性を持たないエッジに使用される値。dataがTrueでもFalseでもない場合にのみ関連します。

戻り値：

edgesEdgeView: エッジ属性のビュー。通常はエッジの(u, v)または(u, v, d)タプルのイテレーションですが、edges[u, v]['foo']のように属性のルックアップにも使用できます。

注記

グラフに存在しないnbunch内のノードは（静かに）無視されます。有向グラフの場合、これはアウトエッジを返します。

例

>>> G = nx.path_graph(3)  # or MultiGraph, etc
>>> G.add_edge(2, 3, weight=5)
>>> [e for e in G.edges]
[(0, 1), (1, 2), (2, 3)]
>>> G.edges.data()  # default data is {} (empty dict)
EdgeDataView([(0, 1, {}), (1, 2, {}), (2, 3, {'weight': 5})])
>>> G.edges.data("weight", default=1)
EdgeDataView([(0, 1, 1), (1, 2, 1), (2, 3, 5)])
>>> G.edges([0, 3])  # only edges from these nodes
EdgeDataView([(0, 1), (3, 2)])
>>> G.edges(0)  # only edges from node 0
EdgeDataView([(0, 1)])

fresh_copy()[source]#

同一のデータ構造を持つ新しいコピーグラフを返します。

新しいコピーには、ノード、エッジ、グラフ属性がありません。現在のグラフと同じデータ構造です。このメソッドは、通常、グラフの空のバージョンを作成するために使用されます。

これは、Networkx v2でGraphをサブクラス化する場合に必要であり、v1では問題を引き起こしません。「1.xから2.xへの移行」ドキュメントに詳細が記載されています。

With the new GraphViews (SubGraph, ReversedGraph, etc)
you can't assume that ``G.__class__()`` will create a new
instance of the same graph type as ``G``. In fact, the
call signature for ``__class__`` differs depending on
whether ``G`` is a view or a base class. For v2.x you
should use ``G.fresh_copy()`` to create a null graph of
the correct type---ready to fill with nodes and edges.

get_edge_data(u, v, default=None)[source]#

エッジ(u, v)に関連付けられた属性辞書を返します。

エッジが存在しない場合に例外を返す代わりにデフォルト値を返す点を除いて、G[u][v] と同一です。

パラメータ：

u, vノード
default: 任意のPythonオブジェクト (default=None): エッジ(u, v)が見つからない場合に返す値。

戻り値：

edge_dict辞書: エッジ属性辞書。

例

>>> G = nx.path_graph(4)  # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G[0][1]
{}

警告: G[u][v]への代入は許可されていません。しかし、G[u][v]['foo']のような属性への代入は安全です。

>>> G[0][1]["weight"] = 7
>>> G[0][1]["weight"]
7
>>> G[1][0]["weight"]
7

>>> G = nx.path_graph(4)  # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.get_edge_data(0, 1)  # default edge data is {}
{}
>>> e = (0, 1)
>>> G.get_edge_data(*e)  # tuple form
{}
>>> G.get_edge_data("a", "b", default=0)  # edge not in graph, return 0
0

graph_attr_dict_factory#: dictのエイリアス

has_edge(u, v)[source]#

エッジ(u, v)がグラフ内にある場合、Trueを返します。

v in G[u] と同じですが、KeyError例外は発生しません。

パラメータ：

u, vノード: ノードは、例えば、文字列または数値です。ノードは、ハッシュ可能（そしてNoneではない）Pythonオブジェクトである必要があります。

戻り値：

edge_indbool: エッジがグラフ内にある場合はTrue、それ以外の場合はFalse。

例

>>> G = nx.path_graph(4)  # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.has_edge(0, 1)  # using two nodes
True
>>> e = (0, 1)
>>> G.has_edge(*e)  #  e is a 2-tuple (u, v)
True
>>> e = (0, 1, {"weight": 7})
>>> G.has_edge(*e[:2])  # e is a 3-tuple (u, v, data_dictionary)
True

以下の構文は同等です。

>>> G.has_edge(0, 1)
True
>>> 1 in G[0]  # though this gives KeyError if 0 not in G
True

has_node(n)[source]#

グラフにノードnが含まれている場合、Trueを返します。

n in G と同一です。

パラメータ：

nノード

例

>>> G = nx.path_graph(3)  # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.has_node(0)
True

より読みやすく、シンプルな使用方法です。

>>> 0 in G
True

is_directed()[source]#: グラフが有向グラフの場合はTrue、そうでない場合はFalseを返します。

is_multigraph()[source]#: グラフがマルチグラフの場合はTrue、そうでない場合はFalseを返します。

merge_nodes(src, dst, weight_func=<function min_weight>, in_place=True, extra_arguments=None, extra_keywords=None)[source]#

ノードsrcとdstをマージします。

新しい結合ノードは、srcとdstのすべての隣接ノードに隣接します。weight_funcは、新しいノードに接続するエッジの重みを決定するために呼び出されます。

パラメータ：

src, dstint: マージするノード。
weight_funccallable, optional: 新しいノードに接続するエッジの属性を決定する関数。 srcとdstの各隣接ノードnに対して、weight_funcは次のように呼び出されます。weight_func(src, dst, n, *extra_arguments, **extra_keywords)。src、dst、nは、networkx.GraphのサブクラスであるRAGオブジェクト内の頂点のIDです。結果のエッジの属性の辞書を返すことが期待されます。
in_placebool, optional: Trueに設定されている場合、マージされたノードのIDはdstになります。そうでない場合、マージされたノードは新しいIDを持ち、それが返されます。
extra_argumentssequence, optional: weight_funcに渡される追加の位置引数のシーケンス。
extra_keywordsdictionary, optional: weight_funcに渡されるキーワード引数の辞書。

戻り値：

idint: 新しいノードのID。

注記

in_placeがFalseの場合、結果のノードはdstではなく、新しいIDを持ちます。

property name#

グラフの文字列識別子。

このグラフ属性は、文字列"name"でキー付けされた属性辞書G.graph、および属性（技術的にはプロパティ）G.nameに表示されます。これは完全にユーザーが制御できます。

nbunch_iter(nbunch=None)[source]#

nbunchに含まれ、グラフにも存在するノードを反復処理するイテレータを返します。

nbunch内のノードはグラフのメンバーシップについてチェックされ、そうでない場合は静かに無視されます。

パラメータ：

nbunch単一ノード、コンテナ、またはすべてのノード（デフォルト=すべてのノード）: このビューは、これらのノードに接続するエッジのみを報告します。

戻り値：

niterイテレータ: nbunch内のノードで、グラフにも存在するノードを反復処理するイテレータ。nbunchがNoneの場合、グラフ内のすべてのノードを反復処理します。

例外:

NetworkXError: nbunchがノードまたはノードのシーケンスでない場合。nbunch内のノードがハッシュ可能でない場合。

参照

Graph.__iter__

注記

nbunchがイテレータの場合、返されるイテレータはnbunchから直接値を生成し、nbunchが使い果たされると使い果たされます。

nbunchが単一のノードかどうかをテストするには、このルーチンで処理した後でも「if nbunch in self:」を使用できます。

nbunchがノードまたは（空の可能性のある）シーケンス/イテレータ、またはNoneでない場合、NetworkXErrorが発生します。また、nbunch内のオブジェクトがハッシュ可能でない場合も、NetworkXErrorが発生します。

neighbors(n)[source]#

ノードnのすべての隣接ノードをイテレータとして返します。

これはiter(G[n])と同じです。

パラメータ：

nノード: グラフ内のノード

戻り値：

neighborsイテレータ: ノードnのすべての隣接ノードのイテレータ

例外:

NetworkXError: ノードnがグラフに存在しない場合。

注記

隣接ノードにアクセスする他の方法としては、G.adj[n]またはG[n]があります。

>>> G = nx.Graph()  # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_edge("a", "b", weight=7)
>>> G["a"]
AtlasView({'b': {'weight': 7}})
>>> G = nx.path_graph(4)
>>> [n for n in G[0]]
[1]

例

>>> G = nx.path_graph(4)  # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> [n for n in G.neighbors(0)]
[1]

next_id()[source]#

挿入される新しいノードのidを返します。

現在の実装では、最大のidより1つ大きい値を返します。

戻り値：

idint: 挿入される新しいノードのid

node_attr_dict_factory#: dictのエイリアス

node_dict_factory#: dictのエイリアス

property nodes#

グラフのNodeViewをG.nodesまたはG.nodes()として返します。

データの参照や集合演算にはG.nodesとして使用できます。G.nodes(data='color', default=None)として使用して、特定のノードデータは返しますが集合演算は行わないNodeDataViewを返すこともできます。また、G.nodes.items()で(node, nodedata)の2タプルを反復処理し、G.nodes[3]['foo']でノード3のfoo属性の値を取得する辞書のようなインターフェースも提供します。さらに、ビューG.nodes.data('foo')は各ノードのfoo属性への辞書のようなインターフェースを提供します。G.nodes.data('foo', default=1)は、foo属性を持たないノードのデフォルト値を提供します。

パラメータ：

data文字列またはbool、オプション（デフォルト=False）: 2タプル(n, ddict[data])で返されるノード属性。Trueの場合、ノード属性辞書全体を(n, ddict)として返します。Falseの場合、ノードnのみを返します。
default値、オプション（デフォルト=None）: 要求された属性を持たないノードに使用される値。dataがTrueまたはFalseでない場合にのみ関連します。

戻り値：

NodeView

ノードに対する集合演算と、ノード属性辞書の参照と、NodeDataViewを取得するための呼び出しを許可します。NodeDataViewは(n, data)を反復処理し、集合演算は行いません。NodeViewはnを反復処理し、集合演算を含みます。

呼び出された場合、dataがFalseの場合、ノードのイテレータを返します。それ以外の場合は、属性がdataで指定された2タプル(ノード、属性値)のイテレータを返します。dataがTrueの場合、属性はデータ辞書全体になります。

注記

ノードデータが不要な場合は、for n in Gまたはlist(G)を使用する方がシンプルで同等です。

例

グラフ内のすべてのノードのリストを取得する2つの簡単な方法があります。

>>> G = nx.path_graph(3)
>>> list(G.nodes)
[0, 1, 2]
>>> list(G)
[0, 1, 2]

ノードデータとノードを一緒に取得するには

>>> G.add_node(1, time="5pm")
>>> G.nodes[0]["foo"] = "bar"
>>> list(G.nodes(data=True))
[(0, {'foo': 'bar'}), (1, {'time': '5pm'}), (2, {})]
>>> list(G.nodes.data())
[(0, {'foo': 'bar'}), (1, {'time': '5pm'}), (2, {})]

>>> list(G.nodes(data="foo"))
[(0, 'bar'), (1, None), (2, None)]
>>> list(G.nodes.data("foo"))
[(0, 'bar'), (1, None), (2, None)]

>>> list(G.nodes(data="time"))
[(0, None), (1, '5pm'), (2, None)]
>>> list(G.nodes.data("time"))
[(0, None), (1, '5pm'), (2, None)]

>>> list(G.nodes(data="time", default="Not Available"))
[(0, 'Not Available'), (1, '5pm'), (2, 'Not Available')]
>>> list(G.nodes.data("time", default="Not Available"))
[(0, 'Not Available'), (1, '5pm'), (2, 'Not Available')]

一部のノードが属性を持ち、残りのノードはデフォルトの属性値を持つと仮定される場合、defaultキーワード引数を使用してノード/属性ペアから辞書を作成し、値が決してNoneにならないようにすることができます。

>>> G = nx.Graph()
>>> G.add_node(0)
>>> G.add_node(1, weight=2)
>>> G.add_node(2, weight=3)
>>> dict(G.nodes(data="weight", default=1))
{0: 1, 1: 2, 2: 3}

number_of_edges(u=None, v=None)[source]#

2つのノード間のエッジ数を返します。

パラメータ：

u, vノード、オプション (デフォルト:すべてのエッジ): uとvが指定されている場合、uとv間のエッジ数を返します。それ以外の場合は、すべてのエッジの総数を返します。

戻り値：

nedgesint: グラフ内のエッジの数。ノードuとvが指定されている場合、それらのノード間のエッジ数を返します。グラフが有向グラフの場合、これはuからvへのエッジ数のみを返します。

参照

サイズ

例

無向グラフの場合、このメソッドはグラフ内のエッジの総数をカウントします。

>>> G = nx.path_graph(4)
>>> G.number_of_edges()
3

2つのノードを指定した場合、このメソッドは2つのノードを結ぶエッジの総数をカウントします。

>>> G.number_of_edges(0, 1)
1

有向グラフの場合、このメソッドはuからvへの有向エッジの総数をカウントできます。

>>> G = nx.DiGraph()
>>> G.add_edge(0, 1)
>>> G.add_edge(1, 0)
>>> G.number_of_edges(0, 1)
1

number_of_nodes()[source]#

グラフ内のノード数を返します。

戻り値：

nnodesint: グラフ内のノード数。

参照

次数: 同一のメソッド
__len__: 同一のメソッド

例

>>> G = nx.path_graph(3)  # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.number_of_nodes()
3

order()[source]#

グラフ内のノード数を返します。

戻り値：

nnodesint: グラフ内のノード数。

参照

number_of_nodes: 同一のメソッド
__len__: 同一のメソッド

例

>>> G = nx.path_graph(3)  # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.order()
3

remove_edge(u, v)[source]#

uとv間のエッジを削除します。

パラメータ：

u, vノード: ノードuとv間のエッジを削除します。

例外:

NetworkXError: uとvの間にエッジが存在しない場合。

参照

remove_edges_from: 複数エッジの削除

例

>>> G = nx.path_graph(4)  # or DiGraph, etc
>>> G.remove_edge(0, 1)
>>> e = (1, 2)
>>> G.remove_edge(*e)  # unpacks e from an edge tuple
>>> e = (2, 3, {"weight": 7})  # an edge with attribute data
>>> G.remove_edge(*e[:2])  # select first part of edge tuple

remove_edges_from(ebunch)[source]#

ebunchで指定されたすべてエッジを削除します。

パラメータ：

ebunch: エッジタプルのリストまたはコンテナ

リストまたはコンテナで指定された各エッジは、グラフから削除されます。エッジは

2タプル(u, v) uとv間のエッジ。

3タプル(u, v, k) kは無視されます。

参照

remove_edge: 単一エッジの削除

注記

ebunch内のエッジがグラフに存在しない場合、サイレントに失敗します。

例

>>> G = nx.path_graph(4)  # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> ebunch = [(1, 2), (2, 3)]
>>> G.remove_edges_from(ebunch)

remove_node(n)[source]#

ノードnを削除します。

ノードnと隣接するすべてのエッジを削除します。存在しないノードを削除しようとすると、例外が発生します。

パラメータ：

nノード: グラフ内のノード

例外:

NetworkXError: nがグラフに存在しない場合。

参照

remove_nodes_from

例

>>> G = nx.path_graph(3)  # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> list(G.edges)
[(0, 1), (1, 2)]
>>> G.remove_node(1)
>>> list(G.edges)
[]

remove_nodes_from(nodes)[source]#

複数のノードを削除します。

パラメータ：

nodes反復可能なコンテナ: ノードのコンテナ(リスト、辞書、集合など)。コンテナ内のノードがグラフに存在しない場合は、サイレントに無視されます。

参照

remove_node

注記

グラフのイテレータを介してノードを削除する場合、変更されているグラフ上でRuntimeErrorがメッセージ「RuntimeError: dictionary changed size during iteration」と共に発生します。これは、反復処理中にグラフの基礎となる辞書が変更された場合に発生します。このエラーを回避するには、list(iterator_of_nodes)を使用してイテレータを別個のオブジェクトに評価し、そのオブジェクトをG.remove_nodes_fromに渡します。

例

>>> G = nx.path_graph(3)  # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> e = list(G.nodes)
>>> e
[0, 1, 2]
>>> G.remove_nodes_from(e)
>>> list(G.nodes)
[]

同じグラフを変更するために使用している場合は、グラフ上のイテレータを評価する

>>> G = nx.Graph([(0, 1), (1, 2), (3, 4)])
>>> # this command will fail, as the graph's dict is modified during iteration
>>> # G.remove_nodes_from(n for n in G.nodes if n < 2)
>>> # this command will work, since the dictionary underlying graph is not modified
>>> G.remove_nodes_from(list(n for n in G.nodes if n < 2))

size(weight=None)[source]#

エッジの数、またはすべてのエッジ重みの合計を返します。

パラメータ：

weight文字列またはNone、オプション（デフォルト=None）: 数値として重みとして使用されるエッジ属性。Noneの場合、各エッジの重みは1です。

戻り値：

size数値

辺の数、または（weightキーワードが指定されている場合）総ウェイトの合計。

weightがNoneの場合、intを返します。それ以外の場合は、float（またはウェイトがより一般的な数値型の場合は、より一般的な数値型）を返します。

参照

辺の数

例

>>> G = nx.path_graph(4)  # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.size()
3

>>> G = nx.Graph()  # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_edge("a", "b", weight=2)
>>> G.add_edge("b", "c", weight=4)
>>> G.size()
2
>>> G.size(weight="weight")
6.0

subgraph(nodes)[source]#

nodesで指定されたノードによって誘導される部分グラフのSubGraphビューを返します。

グラフの誘導部分グラフには、nodes内のノードと、それらのノード間の辺が含まれます。

パラメータ：

nodesリスト、反復可能オブジェクト: 一度反復処理されるノードのコンテナ。

戻り値：

GSubGraphビュー: グラフの部分グラフビューです。グラフ構造は変更できませんが、ノード/エッジ属性は変更でき、元のグラフと共有されます。

注記

グラフ、エッジ、ノードの属性は、元のグラフと共有されます。グラフ構造の変更はビューによって制限されますが、属性の変更は元のグラフに反映されます。

エッジ/ノード属性の独自の複製を含む部分グラフを作成するには、次のようにします。G.subgraph(nodes).copy()

グラフを部分グラフにインプレースで縮小するには、ノードを削除できます。G.remove_nodes_from([n for n in G if n not in set(nodes)])

部分グラフビューは、必ずしも必要なものではありません。誘導された辺を見る以上のことをしたい場合のほとんどでは、次のようなコードで部分グラフを独自のグラフとして作成する方が理にかなっています。

# Create a subgraph SG based on a (possibly multigraph) G
SG = G.__class__()
SG.add_nodes_from((n, G.nodes[n]) for n in largest_wcc)
if SG.is_multigraph():
    SG.add_edges_from(
        (n, nbr, key, d)
        for n, nbrs in G.adj.items()
        if n in largest_wcc
        for nbr, keydict in nbrs.items()
        if nbr in largest_wcc
        for key, d in keydict.items()
    )
else:
    SG.add_edges_from(
        (n, nbr, d)
        for n, nbrs in G.adj.items()
        if n in largest_wcc
        for nbr, d in nbrs.items()
        if nbr in largest_wcc
    )
SG.graph.update(G.graph)

例

>>> G = nx.path_graph(4)  # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> H = G.subgraph([0, 1, 2])
>>> list(H.edges)
[(0, 1), (1, 2)]

to_directed(as_view=False)[source]#

グラフの有向表現を返します。

戻り値：

G有向グラフ: 同じ名前、同じノードを持ち、各辺(u, v, data)が2つの有向辺(u, v, data)と(v, u, data)に置き換えられた有向グラフ。

注記

これは、データと参照を完全にコピーしようとするエッジ、ノード、およびグラフ属性の「deepcopy」を返します。

これは、同様のD=DiGraph(G)とは対照的であり、データの浅いコピーを返します。

浅いコピーと深いコピーの詳細については、Pythonのcopyモジュールを参照してください。https://docs.python.org/3/library/copy.html.

警告: データ構造で辞書のようなオブジェクトを使用するためにGraphをサブクラス化した場合、それらの変更はこのメソッドによって作成されたDiGraphには転送されません。

例

>>> G = nx.Graph()  # or MultiGraph, etc
>>> G.add_edge(0, 1)
>>> H = G.to_directed()
>>> list(H.edges)
[(0, 1), (1, 0)]

既に有向の場合、(深い)コピーを返します。

>>> G = nx.DiGraph()  # or MultiDiGraph, etc
>>> G.add_edge(0, 1)
>>> H = G.to_directed()
>>> list(H.edges)
[(0, 1)]

to_directed_class()[source]#

空の有向コピーに使用するクラスを返します。

基本クラスをサブクラス化した場合、to_directed()コピーに使用する有向クラスを指定するためにこれを使用します。

to_undirected(as_view=False)[source]#

グラフの無向コピーを返します。

パラメータ：

as_viewbool (オプション、デフォルト=False): Trueの場合、元の無向グラフのビューを返します。

戻り値：

GGraph/MultiGraph: グラフのdeepcopy。

参照

Graph、copy、add_edge、add_edges_from

注記

これは、データと参照を完全にコピーしようとするエッジ、ノード、およびグラフ属性の「deepcopy」を返します。

これは、同様のG = nx.DiGraph(D)とは対照的であり、データの浅いコピーを返します。

浅いコピーと深いコピーの詳細については、Pythonのcopyモジュールを参照してください。https://docs.python.org/3/library/copy.html.

警告: データ構造で辞書のようなオブジェクトを使用するためにDiGraphをサブクラス化した場合、それらの変更はこのメソッドによって作成されたGraphには転送されません。

例

>>> G = nx.path_graph(2)  # or MultiGraph, etc
>>> H = G.to_directed()
>>> list(H.edges)
[(0, 1), (1, 0)]
>>> G2 = H.to_undirected()
>>> list(G2.edges)
[(0, 1)]

to_undirected_class()[source]#

空の無向コピーに使用するクラスを返します。

基本クラスをサブクラス化した場合、to_directed()コピーに使用する有向クラスを指定するためにこれを使用します。

update(edges=None, nodes=None)[source]#

ノード/エッジ/グラフを入力として使用してグラフを更新します。

dict.updateと同様に、このメソッドはグラフを入力として受け取り、グラフのノードとエッジをこのグラフに追加します。また、2つの入力（エッジとノード）を受け取ることができます。最後に、エッジまたはノードのいずれかを受け取ることができます。ノードのみを指定するには、キーワードnodesを使用する必要があります。

エッジとノードのコレクションは、add_edges_from/add_nodes_fromメソッドと同様に扱われます。反復処理されると、2タプル(u, v)または3タプル(u, v, datadict)を生成する必要があります。

パラメータ：

edgesグラフオブジェクト、エッジのコレクション、またはNone: 最初の引数は、グラフまたはいくつかのエッジにすることができます。nodesとedgesという属性を持つ場合、グラフのようなオブジェクトと見なされ、それらの属性はグラフに追加されるノードとエッジのコレクションとして使用されます。最初の引数にそれらの属性がない場合、エッジのコレクションとして扱われ、グラフに追加されます。最初の引数がNoneの場合、エッジは追加されません。
nodesノードのコレクション、またはNone: 2番目の引数は、Noneでない限り、グラフに追加されるノードのコレクションとして扱われます。edges is Noneとnodes is Noneの場合は例外が発生します。最初の引数がグラフの場合、nodesは無視されます。

参照

add_edges_from: グラフに複数のエッジを追加します。
add_nodes_from: グラフに複数のノードを追加します。

注記

隣接構造を使用してグラフを更新する場合は、隣接構造からエッジ/ノードを取得するのは簡単です。次の例は一般的なケースを示していますが、隣接構造がわずかに異なる場合があり、これらの例を調整する必要がある場合があります。

>>> # dict-of-set/list/tuple
>>> adj = {1: {2, 3}, 2: {1, 3}, 3: {1, 2}}
>>> e = [(u, v) for u, nbrs in adj.items() for v in nbrs]
>>> G.update(edges=e, nodes=adj)

>>> DG = nx.DiGraph()
>>> # dict-of-dict-of-attribute
>>> adj = {1: {2: 1.3, 3: 0.7}, 2: {1: 1.4}, 3: {1: 0.7}}
>>> e = [
...     (u, v, {"weight": d})
...     for u, nbrs in adj.items()
...     for v, d in nbrs.items()
... ]
>>> DG.update(edges=e, nodes=adj)

>>> # dict-of-dict-of-dict
>>> adj = {1: {2: {"weight": 1.3}, 3: {"color": 0.7, "weight": 1.2}}}
>>> e = [
...     (u, v, {"weight": d})
...     for u, nbrs in adj.items()
...     for v, d in nbrs.items()
... ]
>>> DG.update(edges=e, nodes=adj)

>>> # predecessor adjacency (dict-of-set)
>>> pred = {1: {2, 3}, 2: {3}, 3: {3}}
>>> e = [(v, u) for u, nbrs in pred.items() for v in nbrs]

>>> # MultiGraph dict-of-dict-of-dict-of-attribute
>>> MDG = nx.MultiDiGraph()
>>> adj = {
...     1: {2: {0: {"weight": 1.3}, 1: {"weight": 1.2}}},
...     3: {2: {0: {"weight": 0.7}}},
... }
>>> e = [
...     (u, v, ekey, d)
...     for u, nbrs in adj.items()
...     for v, keydict in nbrs.items()
...     for ekey, d in keydict.items()
... ]
>>> MDG.update(edges=e)

例

>>> G = nx.path_graph(5)
>>> G.update(nx.complete_graph(range(4, 10)))
>>> from itertools import combinations
>>> edges = (
...     (u, v, {"power": u * v})
...     for u, v in combinations(range(10, 20), 2)
...     if u * v < 225
... )
>>> nodes = [1000]  # for singleton, use a container
>>> G.update(edges, nodes)

skimage.graph#

`skimage.graph`#