skimage.feature#
特徴検出と抽出、例:テクスチャ解析、コーナーなど。
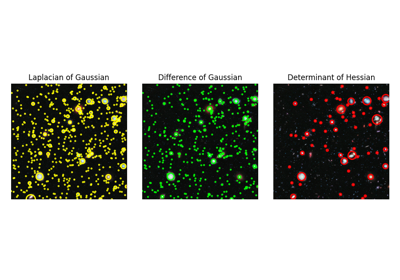
与えられたグレースケール画像内のブロブを検出します。 |
|
与えられたグレースケール画像内のブロブを検出します。 |
|
与えられたグレースケール画像内のブロブを検出します。 |
|
Cannyアルゴリズムを使用して画像のエッジをフィルタリングします。 |
|
与えられた画像に対してFASTコーナーを抽出します。 |
|
Foerstnerコーナー測定応答画像を計算します。 |
|
Harrisコーナー測定応答画像を計算します。 |
|
KitchenとRosenfeldのコーナー測定応答画像を計算します。 |
|
Moravecコーナー測定応答画像を計算します。 |
|
コーナーの方向を計算します。 |
|
コーナー測定応答画像内のピークを検出します。 |
|
Shi-Tomasi(Kanade-Tomasi)コーナー測定応答画像を計算します。 |
|
コーナーのサブピクセル位置を決定します。 |
|
与えられた画像に対してDAISY特徴記述子を密に抽出します。 |
|
Haar様特徴の可視化。 |
|
マルチブロックローカルバイナリパターン可視化。 |
|
いくつかの記述子/ベクトルと、関連する推定GMMが与えられたとき、Fisherベクトルを計算します。 |
|
グレースケール共起行列を計算します。 |
|
GLCMのテクスチャプロパティを計算します。 |
|
積分画像の関心領域(ROI)に対するHaar様特徴を計算します。 |
|
Haar様特徴の座標を計算します。 |
|
ヘッセ行列を計算します。 |
|
画像全体の近似ヘッセ行列式を計算します。 |
|
ヘッセ行列の固有値を計算します。 |
|
与えられた画像に対して、方向勾配のヒストグラム(HOG)を抽出します。 |
|
記述子のセットとモード数(つまり、ガウス関数)が与えられたとき、ガウス混合モデル(GMM)を推定します。 |
|
画像のローカルバイナリパターン(LBP)を計算します。 |
|
記述子のブルートフォースマッチング。 |
|
正規化相関を使用して、テンプレートを2Dまたは3D画像にマッチングします。 |
|
マルチブロックローカルバイナリパターン(MB-LBP)。 |
|
単一または多チャネルのnd画像用のローカル特徴。 |
|
画像内のピークを座標リストとして検出します。 |
|
2つの画像間のマッチした特徴をプロットします。 |
|
形状インデックスを計算します。 |
|
2乗差の合計を使用して構造テンソルを計算します。 |
|
構造テンソルの固有値を計算します。 |
|
BRIEFバイナリ記述子抽出器。 |
|
CENSUREキーポイント検出器。 |
|
オブジェクト検出に使用される分類器のカスケードのクラス。 |
|
方向付けされたFASTおよび回転されたBRIEF特徴検出器とバイナリ記述子抽出器。 |
|
SIFT特徴検出および記述子抽出。 |
- skimage.feature.blob_dog(image, min_sigma=1, max_sigma=50, sigma_ratio=1.6, threshold=0.5, overlap=0.5, *, threshold_rel=None, exclude_border=False)[ソース]#
与えられたグレースケール画像内のブロブを検出します。
ブロブは、ガウシアン差分(DoG)法[1]、[2]を使用して検出されます。検出された各ブロブについて、メソッドはその座標と、ブロブを検出したガウスカーネルの標準偏差を返します。
- パラメータ:
- imagendarray
入力グレースケール画像。ブロブは、暗い背景の明るい(黒の白)であると想定されます。
- min_sigmaスカラーまたはスカラーのシーケンス、オプション
ガウスカーネルの最小標準偏差。小さいブロブを検出するには、これを低く保ちます。ガウスフィルターの標準偏差は、各軸にシーケンスとして、または単一の数値として指定されます。この場合、すべての軸で等しくなります。
- max_sigmaスカラーまたはスカラーのシーケンス、オプション
ガウスカーネルの最大標準偏差。より大きなブロブを検出するには、これを高く保ちます。ガウスフィルターの標準偏差は、各軸にシーケンスとして、または単一の数値として指定されます。この場合、すべての軸で等しくなります。
- sigma_ratiofloat、オプション
ガウシアン差分を計算するために使用されるガウスカーネルの標準偏差の比率
- thresholdfloatまたはNone、オプション
スケール空間最大値の絶対下限。
thresholdよりも小さいローカル最大値は無視されます。強度が低いブロブを検出するには、これを減らします。threshold_relも指定されている場合、どちらかのしきい値が大きい方が使用されます。Noneの場合、threshold_relが代わりに使用されます。- overlapfloat、オプション
0から1までの値。2つのブロブの領域が
thresholdよりも大きい割合で重なっている場合、小さいブロブは削除されます。- threshold_relfloatまたはNone、オプション
ピークの最小強度。
max(dog_space) * threshold_relとして計算されます。ここで、dog_spaceは内部で計算されたガウシアン差分(DoG)画像のスタックを指します。これは0から1の間の値にする必要があります。Noneの場合、thresholdが代わりに使用されます。- exclude_borderintのタプル、int、またはFalse、オプション
intのタプルの場合、タプルの長さは入力配列の次元と一致する必要があります。タプルの各要素は、その次元に沿った画像の境界の
exclude_borderピクセル以内からピークを除外します。ゼロ以外のintの場合、exclude_borderは、画像の境界のexclude_borderピクセル以内からピークを除外します。ゼロまたはFalseの場合、ピークは境界からの距離に関係なく識別されます。
- 戻り値:
- A(n, image.ndim + sigma) ndarray
各行が2D画像の場合は2つの座標値、3D画像の場合は3つの座標値、および使用されたsigma(s)を表す2D配列。単一のsigmaが渡されると、出力は次のようになります。
(r, c, sigma)または(p, r, c, sigma)。ここで、(r, c)または(p, r, c)はブロブの座標であり、sigmaはブロブを検出したガウスカーネルの標準偏差です。異方性ガウス(次元ごとのシグマ)が使用されている場合、検出されたシグマは各次元に対して返されます。
注釈
各ブロブの半径は、2D画像の場合はおよそ\(\sqrt{2}\sigma\)、3D画像の場合はおよそ\(\sqrt{3}\sigma\)です。
参考文献
[2]Lowe, D. G. “Distinctive Image Features from Scale-Invariant Keypoints.” International Journal of Computer Vision 60, 91–110 (2004). https://www.cs.ubc.ca/~lowe/papers/ijcv04.pdf DOI:10.1023/B:VISI.0000029664.99615.94
例
>>> from skimage import data, feature >>> coins = data.coins() >>> feature.blob_dog(coins, threshold=.05, min_sigma=10, max_sigma=40) array([[128., 155., 10.], [198., 155., 10.], [124., 338., 10.], [127., 102., 10.], [193., 281., 10.], [126., 208., 10.], [267., 115., 10.], [197., 102., 10.], [198., 215., 10.], [123., 279., 10.], [126., 46., 10.], [259., 247., 10.], [196., 43., 10.], [ 54., 276., 10.], [267., 358., 10.], [ 58., 100., 10.], [259., 305., 10.], [185., 347., 16.], [261., 174., 16.], [ 46., 336., 16.], [ 54., 217., 10.], [ 55., 157., 10.], [ 57., 41., 10.], [260., 47., 16.]])
- skimage.feature.blob_doh(image, min_sigma=1, max_sigma=30, num_sigma=10, threshold=0.01, overlap=0.5, log_scale=False, *, threshold_rel=None)[ソース]#
与えられたグレースケール画像内のブロブを検出します。
ブロブは、ヘッセ行列の行列式法 [1] を用いて検出されます。検出された各ブロブに対して、このメソッドはその座標と、ブロブを検出したヘッセ行列に使用されたガウスカーネルの標準偏差を返します。ヘッセ行列の行列式は、[2] を用いて近似されます。
- パラメータ:
- image2D ndarray
入力グレースケール画像。ブロブは明るい背景に暗いブロブ、またはその逆のいずれでも可能です。
- min_sigmafloat, optional
ヘッセ行列の計算に使用するガウスカーネルの最小標準偏差。小さいブロブを検出するには、この値を小さくしてください。
- max_sigmafloat, optional
ヘッセ行列の計算に使用するガウスカーネルの最大標準偏差。大きいブロブを検出するには、この値を大きくしてください。
- num_sigmaint, optional
min_sigmaとmax_sigmaの間で考慮する標準偏差の中間値の数。- thresholdfloatまたはNone、オプション
スケール空間最大値の絶対下限。
thresholdよりも小さいローカル最大値は無視されます。強度が低いブロブを検出するには、これを減らします。threshold_relも指定されている場合、どちらかのしきい値が大きい方が使用されます。Noneの場合、threshold_relが代わりに使用されます。- overlapfloat、オプション
0から1までの値。2つのブロブの領域が
thresholdよりも大きい割合で重なっている場合、小さいブロブは削除されます。- log_scalebool, optional
設定すると、標準偏差の中間値は、底
10の対数スケールを用いて補間されます。そうでない場合は、線形補間が使用されます。- threshold_relfloatまたはNone、オプション
ピークの最小強度。内部で計算されるヘッセ行列の行列式(DoH)画像のスタックを指す
doh_spaceにおいて、max(doh_space) * threshold_relとして計算されます。これは 0 から 1 の間の値である必要があります。None の場合、代わりにthresholdが使用されます。
- 戻り値:
- A(n, 3) ndarray
各行が 3 つの値、
(y,x,sigma)を表す 2 次元配列。(y,x)はブロブの座標、sigmaはブロブを検出したヘッセ行列のガウスカーネルの標準偏差です。
注釈
各ブロブの半径はほぼ
sigmaです。ヘッセ行列の行列式の計算は標準偏差に依存しません。したがって、大きなブロブを検出しても時間がかかることはありません。メソッドblob_dog()およびblob_log()では、大きなsigmaのガウス関数の計算に時間がかかります。欠点は、ヘッセ行列の行列式の近似に使用されるボックスフィルターのため、このメソッドを3px未満の半径のブロブを検出するために使用できないことです。参考文献
[2]Herbert Bay, Andreas Ess, Tinne Tuytelaars, Luc Van Gool, “SURF: Speeded Up Robust Features” ftp://ftp.vision.ee.ethz.ch/publications/articles/eth_biwi_00517.pdf
例
>>> from skimage import data, feature >>> img = data.coins() >>> feature.blob_doh(img) array([[197. , 153. , 20.33333333], [124. , 336. , 20.33333333], [126. , 153. , 20.33333333], [195. , 100. , 23.55555556], [192. , 212. , 23.55555556], [121. , 271. , 30. ], [126. , 101. , 20.33333333], [193. , 275. , 23.55555556], [123. , 205. , 20.33333333], [270. , 363. , 30. ], [265. , 113. , 23.55555556], [262. , 243. , 23.55555556], [185. , 348. , 30. ], [156. , 302. , 30. ], [123. , 44. , 23.55555556], [260. , 173. , 30. ], [197. , 44. , 20.33333333]])
- skimage.feature.blob_log(image, min_sigma=1, max_sigma=50, num_sigma=10, threshold=0.2, overlap=0.5, log_scale=False, *, threshold_rel=None, exclude_border=False)[source]#
与えられたグレースケール画像内のブロブを検出します。
ブロブは、ガウスのラプラシアン(LoG)法 [1] を用いて検出されます。検出された各ブロブに対して、このメソッドはその座標と、ブロブを検出したガウスカーネルの標準偏差を返します。
- パラメータ:
- imagendarray
入力グレースケール画像。ブロブは、暗い背景の明るい(黒の白)であると想定されます。
- min_sigmaスカラーまたはスカラーのシーケンス、オプション
ガウスカーネルの最小標準偏差。小さいブロブを検出するには、この値を小さくしてください。ガウスフィルターの標準偏差は、各軸に対してシーケンスとして、またはすべての軸で等しい場合は単一の数値として指定されます。
- max_sigmaスカラーまたはスカラーのシーケンス、オプション
ガウスカーネルの最大標準偏差。より大きなブロブを検出するには、これを高く保ちます。ガウスフィルターの標準偏差は、各軸にシーケンスとして、または単一の数値として指定されます。この場合、すべての軸で等しくなります。
- num_sigmaint, optional
min_sigmaとmax_sigmaの間で考慮する標準偏差の中間値の数。- thresholdfloatまたはNone、オプション
スケール空間最大値の絶対下限。
thresholdよりも小さいローカル最大値は無視されます。強度が低いブロブを検出するには、これを減らします。threshold_relも指定されている場合、どちらかのしきい値が大きい方が使用されます。Noneの場合、threshold_relが代わりに使用されます。- overlapfloat、オプション
0から1までの値。2つのブロブの領域が
thresholdよりも大きい割合で重なっている場合、小さいブロブは削除されます。- log_scalebool, optional
設定すると、標準偏差の中間値は、底
10の対数スケールを用いて補間されます。そうでない場合は、線形補間が使用されます。- threshold_relfloatまたはNone、オプション
ピークの最小強度。内部で計算されるラプラシアンオブガウシアン(LoG)画像のスタックを指す
log_spaceにおいて、max(log_space) * threshold_relとして計算されます。これは 0 から 1 の間の値である必要があります。None の場合、代わりにthresholdが使用されます。- exclude_borderintのタプル、int、またはFalse、オプション
intのタプルの場合、タプルの長さは入力配列の次元と一致する必要があります。タプルの各要素は、その次元に沿った画像の境界の
exclude_borderピクセル以内からピークを除外します。ゼロ以外のintの場合、exclude_borderは、画像の境界のexclude_borderピクセル以内からピークを除外します。ゼロまたはFalseの場合、ピークは境界からの距離に関係なく識別されます。
- 戻り値:
- A(n, image.ndim + sigma) ndarray
各行が2D画像の場合は2つの座標値、3D画像の場合は3つの座標値、および使用されたsigma(s)を表す2D配列。単一のsigmaが渡されると、出力は次のようになります。
(r, c, sigma)または(p, r, c, sigma)。ここで、(r, c)または(p, r, c)はブロブの座標であり、sigmaはブロブを検出したガウスカーネルの標準偏差です。異方性ガウス(次元ごとのシグマ)が使用されている場合、検出されたシグマは各次元に対して返されます。
注釈
各ブロブの半径は、2D画像の場合はおよそ\(\sqrt{2}\sigma\)、3D画像の場合はおよそ\(\sqrt{3}\sigma\)です。
参考文献
例
>>> from skimage import data, feature, exposure >>> img = data.coins() >>> img = exposure.equalize_hist(img) # improves detection >>> feature.blob_log(img, threshold = .3) array([[124. , 336. , 11.88888889], [198. , 155. , 11.88888889], [194. , 213. , 17.33333333], [121. , 272. , 17.33333333], [263. , 244. , 17.33333333], [194. , 276. , 17.33333333], [266. , 115. , 11.88888889], [128. , 154. , 11.88888889], [260. , 174. , 17.33333333], [198. , 103. , 11.88888889], [126. , 208. , 11.88888889], [127. , 102. , 11.88888889], [263. , 302. , 17.33333333], [197. , 44. , 11.88888889], [185. , 344. , 17.33333333], [126. , 46. , 11.88888889], [113. , 323. , 1. ]])
- skimage.feature.canny(image, sigma=1.0, low_threshold=None, high_threshold=None, mask=None, use_quantiles=False, *, mode='constant', cval=0.0)[source]#
Cannyアルゴリズムを使用して画像のエッジをフィルタリングします。
- パラメータ:
- image2D array
エッジを検出するグレースケール入力画像。任意のdtypeを使用できます。
- sigmafloat, optional
ガウスフィルターの標準偏差。
- low_thresholdfloat, optional
ヒステリシスしきい値処理(エッジのリンク)の下限。Noneの場合、low_thresholdはdtypeの最大値の10%に設定されます。
- high_thresholdfloat, optional
ヒステリシスしきい値処理(エッジのリンク)の上限。Noneの場合、high_thresholdはdtypeの最大値の20%に設定されます。
- maskarray, dtype=bool, optional
Cannyの適用を特定の領域に制限するためのマスク。
- use_quantilesbool, optional
Trueの場合、low_thresholdとhigh_thresholdを、絶対エッジ強度値ではなく、エッジ強度画像の分位数として扱います。Trueの場合、しきい値は範囲 [0, 1] にある必要があります。- modestr, {‘reflect’, ‘constant’, ‘nearest’, ‘mirror’, ‘wrap’}
modeパラメータは、ガウスフィルタリング中に配列の境界をどのように処理するかを決定します。ここで、cvalは mode が ‘constant’ と等しい場合の値です。- cvalfloat, optional
modeが 'constant' の場合、入力のエッジを超えて埋める値。
- 戻り値:
- output2D array (image)
バイナリエッジマップ。
注釈
アルゴリズムの手順は次のとおりです。
sigma幅のガウス関数を使用して画像を平滑化します。水平および垂直のソーベル演算子を適用して、画像内の勾配を取得します。エッジ強度は、勾配のノルムです。
潜在的なエッジを1ピクセル幅の曲線に細くします。まず、各点でのエッジに対する法線を見つけます。これは、X-ソーベルとY-ソーベルの符号と相対的な大きさを調べて、点を水平、垂直、対角、および反対角の4つのカテゴリに分類することによって行われます。次に、法線方向と逆方向に見て、いずれかの方向の値が問題の点よりも大きいかどうかを確認します。法線に最も近い点を選ぶのではなく、補間を使用して点の混合を取得します。
ヒステリシスしきい値処理を実行します。まず、高いしきい値を超えるすべての点をエッジとしてラベル付けします。次に、低いしきい値を超える、ラベル付けされた点に8連結されている点を再帰的にエッジとしてラベル付けします。
参考文献
[1]Canny, J., A Computational Approach To Edge Detection, IEEE Trans. Pattern Analysis and Machine Intelligence, 8:679-714, 1986 DOI:10.1109/TPAMI.1986.4767851
[2]William GreenのCannyチュートリアル https://en.wikipedia.org/wiki/Canny_edge_detector
例
>>> from skimage import feature >>> rng = np.random.default_rng() >>> # Generate noisy image of a square >>> im = np.zeros((256, 256)) >>> im[64:-64, 64:-64] = 1 >>> im += 0.2 * rng.random(im.shape) >>> # First trial with the Canny filter, with the default smoothing >>> edges1 = feature.canny(im) >>> # Increase the smoothing for better results >>> edges2 = feature.canny(im, sigma=3)
- skimage.feature.corner_fast(image, n=12, threshold=0.15)[source]#
与えられた画像に対してFASTコーナーを抽出します。
- パラメータ:
- image(M, N) ndarray
入力画像。
- nint, optional
円上の16ピクセルのうち、テストピクセルに関してすべて明るいか暗いかの連続する最小ピクセル数。円上の点cは、
Ic < Ip - thresholdの場合、テストピクセルpに関して暗く、Ic > Ip + thresholdの場合、明るくなります。FAST-nコーナー検出器のnも表します。- thresholdfloat, optional
円上のピクセルがテストピクセルに関して明るいか、暗いか、または類似しているかを決定する際に使用されるしきい値。コーナーをもっと多く取得したい場合は、しきい値を下げ、その逆も同様です。
- 戻り値:
- responsendarray
FASTコーナー応答画像。
参考文献
[1]Rosten, E., & Drummond, T. (2006, May). Machine learning for high-speed corner detection. In European conference on computer vision (pp. 430-443). Springer, Berlin, Heidelberg. DOI:10.1007/11744023_34 http://www.edwardrosten.com/work/rosten_2006_machine.pdf
[2]Wikipedia, “Features from accelerated segment test”, https://en.wikipedia.org/wiki/Features_from_accelerated_segment_test
例
>>> from skimage.feature import corner_fast, corner_peaks >>> square = np.zeros((12, 12)) >>> square[3:9, 3:9] = 1 >>> square.astype(int) array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0], [0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0], [0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0], [0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0], [0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0], [0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]) >>> corner_peaks(corner_fast(square, 9), min_distance=1) array([[3, 3], [3, 8], [8, 3], [8, 8]])
- skimage.feature.corner_foerstner(image, sigma=1)[ソース]#
Foerstnerコーナー測定応答画像を計算します。
このコーナー検出器は、自己相関行列Aからの情報を使用します。
A = [(imx**2) (imx*imy)] = [Axx Axy] [(imx*imy) (imy**2)] [Axy Ayy]
ここで、imxとimyは、ガウシアンフィルターで平均化された一次微分です。コーナーの尺度は、次のように定義されます。
w = det(A) / trace(A) (size of error ellipse) q = 4 * det(A) / trace(A)**2 (roundness of error ellipse)
- パラメータ:
- image(M, N) ndarray
入力画像。
- sigmafloat, optional
自己相関行列の重み関数として使用されるガウシアンカーネルに使用される標準偏差。
- 戻り値:
- wndarray
誤差楕円のサイズ。
- qndarray
誤差楕円の丸み。
参考文献
[1]Förstner, W., & Gülch, E. (1987, June). A fast operator for detection and precise location of distinct points, corners and centres of circular features. In Proc. ISPRS intercommission conference on fast processing of photogrammetric data (pp. 281-305). https://cseweb.ucsd.edu/classes/sp02/cse252/foerstner/foerstner.pdf
例
>>> from skimage.feature import corner_foerstner, corner_peaks >>> square = np.zeros([10, 10]) >>> square[2:8, 2:8] = 1 >>> square.astype(int) array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 1, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 1, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]) >>> w, q = corner_foerstner(square) >>> accuracy_thresh = 0.5 >>> roundness_thresh = 0.3 >>> foerstner = (q > roundness_thresh) * (w > accuracy_thresh) * w >>> corner_peaks(foerstner, min_distance=1) array([[2, 2], [2, 7], [7, 2], [7, 7]])
- skimage.feature.corner_harris(image, method='k', k=0.05, eps=1e-06, sigma=1)[ソース]#
Harrisコーナー測定応答画像を計算します。
このコーナー検出器は、自己相関行列Aからの情報を使用します。
A = [(imx**2) (imx*imy)] = [Axx Axy] [(imx*imy) (imy**2)] [Axy Ayy]
ここで、imxとimyは、ガウシアンフィルターで平均化された一次微分です。コーナーの尺度は、次のように定義されます。
det(A) - k * trace(A)**2
または
2 * det(A) / (trace(A) + eps)
- パラメータ:
- image(M, N) ndarray
入力画像。
- method{‘k’, ‘eps’}, optional
自己相関行列から応答画像を計算する方法。
- kfloat, optional
コーナーをエッジから分離するための感度係数。通常、
[0, 0.2]の範囲です。kの値が小さいほど、シャープなコーナーが検出されます。- epsfloat, optional
正規化係数(ノーブルのコーナー尺度)。
- sigmafloat, optional
自己相関行列の重み関数として使用されるガウシアンカーネルに使用される標準偏差。
- 戻り値:
- responsendarray
ハリスの応答画像。
参考文献
例
>>> from skimage.feature import corner_harris, corner_peaks >>> square = np.zeros([10, 10]) >>> square[2:8, 2:8] = 1 >>> square.astype(int) array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 1, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 1, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]) >>> corner_peaks(corner_harris(square), min_distance=1) array([[2, 2], [2, 7], [7, 2], [7, 7]])
- skimage.feature.corner_kitchen_rosenfeld(image, mode='constant', cval=0)[ソース]#
KitchenとRosenfeldのコーナー測定応答画像を計算します。
コーナー尺度は、次のように計算されます。
(imxx * imy**2 + imyy * imx**2 - 2 * imxy * imx * imy) / (imx**2 + imy**2)
ここで、imxとimyは一次微分、imxx、imxy、imyyは二次微分です。
- パラメータ:
- image(M, N) ndarray
入力画像。
- mode{‘constant’, ‘reflect’, ‘wrap’, ‘nearest’, ‘mirror’}, optional
画像の境界外の値を処理する方法。
- cvalfloat, optional
mode 'constant' と組み合わせて使用される、画像の境界外の値。
- 戻り値:
- responsendarray
キッチンとローゼンフェルドの応答画像。
参考文献
[1]Kitchen, L., & Rosenfeld, A. (1982). Gray-level corner detection. Pattern recognition letters, 1(2), 95-102. DOI:10.1016/0167-8655(82)90020-4
- skimage.feature.corner_moravec(image, window_size=1)[ソース]#
Moravecコーナー測定応答画像を計算します。
これは最も単純なコーナー検出器の1つであり、比較的高速ですが、いくつかの制限があります(例:回転不変ではない)。
- パラメータ:
- image(M, N) ndarray
入力画像。
- window_sizeint, optional
ウィンドウサイズ。
- 戻り値:
- responsendarray
モラベックの応答画像。
参考文献
例
>>> from skimage.feature import corner_moravec >>> square = np.zeros([7, 7]) >>> square[3, 3] = 1 >>> square.astype(int) array([[0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 1, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0]]) >>> corner_moravec(square).astype(int) array([[0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0], [0, 0, 1, 1, 1, 0, 0], [0, 0, 1, 2, 1, 0, 0], [0, 0, 1, 1, 1, 0, 0], [0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0]])
- skimage.feature.corner_orientations(image, corners, mask)[ソース]#
コーナーの方向を計算します。
コーナーの向きは、一次中心モーメント、つまり重心アプローチを使用して計算されます。コーナーの向きは、コーナー座標から、一次中心モーメントを使用して計算されたコーナー周辺の局所的な近傍における強度重心へのベクトルの角度です。
- パラメータ:
- image(M, N) array
入力グレースケール画像。
- corners(K, 2) array
(row, col)としてのコーナー座標。- mask2D array
中心モーメントの計算に使用されるコーナーの局所近傍を定義するマスク。
- 戻り値:
- orientations(K, 1) array
[-pi, pi]の範囲のコーナーの向き。
参考文献
[1]Ethan Rublee, Vincent Rabaud, Kurt Konolige and Gary Bradski “ORB : An efficient alternative to SIFT and SURF” http://www.vision.cs.chubu.ac.jp/CV-R/pdf/Rublee_iccv2011.pdf
[2]Paul L. Rosin, “Measuring Corner Properties” http://users.cs.cf.ac.uk/Paul.Rosin/corner2.pdf
例
>>> from skimage.morphology import octagon >>> from skimage.feature import (corner_fast, corner_peaks, ... corner_orientations) >>> square = np.zeros((12, 12)) >>> square[3:9, 3:9] = 1 >>> square.astype(int) array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0], [0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0], [0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0], [0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0], [0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0], [0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]) >>> corners = corner_peaks(corner_fast(square, 9), min_distance=1) >>> corners array([[3, 3], [3, 8], [8, 3], [8, 8]]) >>> orientations = corner_orientations(square, corners, octagon(3, 2)) >>> np.rad2deg(orientations) array([ 45., 135., -45., -135.])
- skimage.feature.corner_peaks(image, min_distance=1, threshold_abs=None, threshold_rel=None, exclude_border=True, indices=True, num_peaks=inf, footprint=None, labels=None, *, num_peaks_per_label=inf, p_norm=inf)[ソース]#
コーナー測定応答画像内のピークを検出します。
これは、同じアキュムレータ値を持つ複数の接続されたピークを抑制するという点で、
skimage.feature.peak_local_maxとは異なります。- パラメータ:
- image(M, N) ndarray
入力画像。
- min_distanceint, optional
ピークを分離するために許容される最小距離。
- **
skimage.feature.peak_local_max()を参照してください。- p_normfloat
使用するミンコフスキーpノルム。範囲[1, inf]である必要があります。オーバーフローが発生する可能性がある場合、有限の大きなpはValueErrorを引き起こす可能性があります。
infはチェビシェフ距離に対応し、2はユークリッド距離に対応します。
- 戻り値:
- outputndarray または ndarray of bools
indices = Trueの場合:(行、列、…)ピークの座標。indices = Falseの場合:imageのような形状のブール配列。ピークはTrue値で表されます。
注釈
バージョン 0.18 で変更:
threshold_relのデフォルト値がNoneに変更されました。これは、skimage.feature.peak_local_maxがデフォルトを決定することを意味します。これは、threshold_rel=0と同等です。num_peaksの制限は、接続されたピークの抑制前に適用されます。抑制後のピーク数を制限するには、num_peaks=np.infを設定し、この関数の出力を後処理します。例
>>> from skimage.feature import peak_local_max >>> response = np.zeros((5, 5)) >>> response[2:4, 2:4] = 1 >>> response array([[0., 0., 0., 0., 0.], [0., 0., 0., 0., 0.], [0., 0., 1., 1., 0.], [0., 0., 1., 1., 0.], [0., 0., 0., 0., 0.]]) >>> peak_local_max(response) array([[2, 2], [2, 3], [3, 2], [3, 3]]) >>> corner_peaks(response) array([[2, 2]])
- skimage.feature.corner_shi_tomasi(image, sigma=1)[ソース]#
Shi-Tomasi(Kanade-Tomasi)コーナー測定応答画像を計算します。
このコーナー検出器は、自己相関行列Aからの情報を使用します。
A = [(imx**2) (imx*imy)] = [Axx Axy] [(imx*imy) (imy**2)] [Axy Ayy]
ここで、imxとimyは、ガウシアンフィルタで平均化された一次導関数です。コーナーの尺度(corner measure)は、Aの小さい方の固有値として定義されます。
((Axx + Ayy) - sqrt((Axx - Ayy)**2 + 4 * Axy**2)) / 2
- パラメータ:
- image(M, N) ndarray
入力画像。
- sigmafloat, optional
自己相関行列の重み関数として使用されるガウシアンカーネルに使用される標準偏差。
- 戻り値:
- responsendarray
Shi-Tomasiの応答画像。
参考文献
例
>>> from skimage.feature import corner_shi_tomasi, corner_peaks >>> square = np.zeros([10, 10]) >>> square[2:8, 2:8] = 1 >>> square.astype(int) array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 1, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 1, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]) >>> corner_peaks(corner_shi_tomasi(square), min_distance=1) array([[2, 2], [2, 7], [7, 2], [7, 7]])
- skimage.feature.corner_subpix(image, corners, window_size=11, alpha=0.99)[ソース]#
コーナーのサブピクセル位置を決定します。
統計的検定によって、コーナーが2つのエッジの交点として定義されるか、単一のピークとして定義されるかが決定されます。分類結果に応じて、サブピクセルコーナーの位置は、グレー値の局所共分散に基づいて決定されます。どちらかの統計的検定の有意水準が十分でない場合、コーナーを分類できず、出力のサブピクセル位置はNaNに設定されます。
- パラメータ:
- image(M, N) ndarray
入力画像。
- corners(K, 2) ndarray
コーナー座標
(行, 列)。- window_sizeint, optional
サブピクセル推定の検索ウィンドウサイズ。
- alphafloat, optional
コーナー分類の有意水準。
- 戻り値:
- positions(K, 2) ndarray
サブピクセルコーナー位置。「未分類」のコーナーについてはNaN。
参考文献
[1]Förstner, W., & Gülch, E. (1987, June). A fast operator for detection and precise location of distinct points, corners and centres of circular features. In Proc. ISPRS intercommission conference on fast processing of photogrammetric data (pp. 281-305). https://cseweb.ucsd.edu/classes/sp02/cse252/foerstner/foerstner.pdf
例
>>> from skimage.feature import corner_harris, corner_peaks, corner_subpix >>> img = np.zeros((10, 10)) >>> img[:5, :5] = 1 >>> img[5:, 5:] = 1 >>> img.astype(int) array([[1, 1, 1, 1, 1, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]]) >>> coords = corner_peaks(corner_harris(img), min_distance=2) >>> coords_subpix = corner_subpix(img, coords, window_size=7) >>> coords_subpix array([[4.5, 4.5]])
- skimage.feature.daisy(image, step=4, radius=15, rings=3, histograms=8, orientations=8, normalization='l1', sigmas=None, ring_radii=None, visualize=False)[ソース]#
与えられた画像に対してDAISY特徴記述子を密に抽出します。
DAISYは、高速な密抽出を可能にするように定式化された、SIFTに類似した特徴記述子です。通常、これは bag-of-features の画像表現に実用的です。
この実装はTolaら[1]に従いますが、次の点で異なります。
- パラメータ:
- image(M, N) array
入力画像(グレースケール)。
- stepint, optional
記述子サンプリングポイント間の距離。
- radiusint, optional
最外輪の半径(ピクセル単位)。
- ringsint, optional
リングの数。
- histogramsint, optional
リングごとにサンプリングされるヒストグラムの数。
- orientationsint, optional
ヒストグラムごとの方向(ビン)の数。
- normalization[ ‘l1’ | ‘l2’ | ‘daisy’ | ‘off’ ], optional
記述子を正規化する方法。
‘l1’:各記述子のL1正規化。
‘l2’:各記述子のL2正規化。
‘daisy’:個々のヒストグラムのL2正規化。
‘off’:正規化を無効にします。
- sigmasfloat の 1D 配列, optional
中心ヒストグラムとヒストグラムの各リングの空間ガウシアン平滑化の標準偏差。シグマの配列は、中心から外側に向かってソートする必要があります。つまり、最初のシグマ値は中心ヒストグラムの空間平滑化を定義し、最後のシグマ値は最外輪の空間平滑化を定義します。sigmasを指定すると、次のパラメーターが上書きされます。
rings = len(sigmas) - 1- ring_radiiint の 1D 配列, optional
各リングの半径(ピクセル単位)。ring_radiiを指定すると、次の2つのパラメーターが上書きされます。
rings = len(ring_radii)radius = ring_radii[-1]sigmasとring_radiiの両方が与えられた場合、中心ヒストグラムには半径が不要であるため、次の述語を満たす必要があります。
len(ring_radii) == len(sigmas) + 1- visualizebool, optional
DAISY記述子の可視化を生成します。
- 戻り値:
- descsarray
与えられた画像のDAISY記述子のグリッド。配列の次元は(P, Q, R)であり、ここで、
P = ceil((M - radius*2) / step)Q = ceil((N - radius*2) / step)R = (rings * histograms + 1) * orientations- descs_img(M, N, 3) array (visualize==Trueの場合のみ)
DAISY記述子の可視化。
参考文献
- skimage.feature.draw_haar_like_feature(image, r, c, width, height, feature_coord, color_positive_block=(1.0, 0.0, 0.0), color_negative_block=(0.0, 1.0, 0.0), alpha=0.5, max_n_features=None, rng=None)[ソース]#
Haar様特徴の可視化。
- パラメータ:
- image(M, N) ndarray
特徴を計算する必要がある積分画像の領域。
- rint
検出ウィンドウの左上隅の行座標。
- cint
検出ウィンドウの左上隅の列座標。
- widthint
検出ウィンドウの幅。
- heightint
検出ウィンドウの高さ。
- feature_coordタプルのリストまたはNoneのndarray, optional
抽出する座標の配列。これは、機能のサブセットのみを再計算する場合に役立ちます。この場合、
feature_typeは、haar_like_feature_coord()によって返されるように、各機能のタイプを含む配列である必要があります。デフォルトでは、すべての座標が計算されます。- color_positive_block3つのfloatのタプル
正のブロックの色を指定するfloat。対応する値は(R、G、B)値を定義します。デフォルト値は赤(1、0、0)です。
- color_negative_block3つのfloatのタプル
負のブロックの色を指定するfloat。対応する値は(R、G、B)値を定義します。デフォルト値は青(0、1、0)です。
- alphafloat
可視化の不透明度を指定する範囲[0、1]の値。1 - 完全透明、0 - 不透明。
- max_n_featuresint, default=None
返される最大機能数。デフォルトでは、すべての機能が返されます。
- rng{
numpy.random.Generator, int}, optional 擬似乱数ジェネレーター。デフォルトでは、PCG64ジェネレーターが使用されます(
numpy.random.default_rng()を参照)。rngがintの場合、ジェネレーターのシードに使用されます。rngは、利用可能な機能の総数よりも少ない機能のセットを生成する場合に使用されます。
- 戻り値:
- features(M, N), ndarray
異なる機能が追加される画像。
例
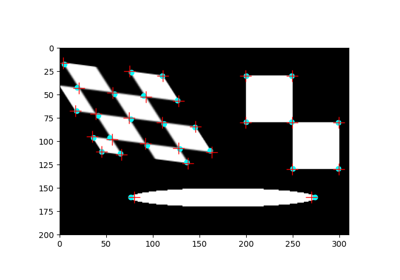
>>> import numpy as np >>> from skimage.feature import haar_like_feature_coord >>> from skimage.feature import draw_haar_like_feature >>> feature_coord, _ = haar_like_feature_coord(2, 2, 'type-4') >>> image = draw_haar_like_feature(np.zeros((2, 2)), ... 0, 0, 2, 2, ... feature_coord, ... max_n_features=1) >>> image array([[[0. , 0.5, 0. ], [0.5, 0. , 0. ]], [[0.5, 0. , 0. ], [0. , 0.5, 0. ]]])
- skimage.feature.draw_multiblock_lbp(image, r, c, width, height, lbp_code=0, color_greater_block=(1, 1, 1), color_less_block=(0, 0.69, 0.96), alpha=0.5)[ソース]#
マルチブロックローカルバイナリパターン可視化。
合計値が大きいブロックは、アルファブレンドされた白い長方形で色付けされ、合計値が小さいブロックは、アルファブレンドされたシアンで色付けされます。色と
alphaパラメータは変更できます。- パラメータ:
- imagefloat または uint の ndarray
パターンを可視化する画像。
- rint
特徴量を含む長方形の左上隅の行座標。
- cint
特徴量を含む長方形の左上隅の列座標。
- widthint
特徴量の計算に使用される 9 つの等しい長方形のうちの 1 つの幅。
- heightint
特徴量の計算に使用される 9 つの等しい長方形のうちの 1 つの高さ。
- lbp_codeint
可視化する特徴量の記述子。指定しない場合は、値が 0 の記述子が使用されます。
- color_greater_block3 つの float のタプル
強度値が大きいブロックの色を指定する float。それらは [0, 1] の範囲にある必要があります。対応する値は (R, G, B) の値を定義します。デフォルト値は白 (1, 1, 1) です。
- color_greater_block3 つの float のタプル
強度値が大きいブロックの色を指定する float。それらは [0, 1] の範囲にある必要があります。対応する値は (R, G, B) の値を定義します。デフォルト値はシアン (0, 0.69, 0.96) です。
- alphafloat
可視化の不透明度を指定する範囲[0、1]の値。1 - 完全透明、0 - 不透明。
- 戻り値:
- outputfloat の ndarray
MB-LBP 可視化付きの画像。
参考文献
[1]L. Zhang, R. Chu, S. Xiang, S. Liao, S.Z. Li. “Face Detection Based on Multi-Block LBP Representation”, In Proceedings: Advances in Biometrics, International Conference, ICB 2007, Seoul, Korea. http://www.cbsr.ia.ac.cn/users/scliao/papers/Zhang-ICB07-MBLBP.pdf DOI:10.1007/978-3-540-74549-5_2
- skimage.feature.fisher_vector(descriptors, gmm, *, improved=False, alpha=0.5)[ソース]#
いくつかの記述子/ベクトルと、関連する推定GMMが与えられたとき、Fisherベクトルを計算します。
- パラメータ:
- descriptorsnp.ndarray, shape=(n_descriptors, descriptor_length)
フィッシャーベクトル表現を計算する記述子の NumPy 配列。
- gmm
sklearn.mixture.GaussianMixture フィッシャーベクトルの計算に必要なパラメータを含む、推定された GMM オブジェクト。
- improvedbool, default=False
改良されたフィッシャーベクトルを計算するかどうかを示すフラグ。改良されたフィッシャーベクトルは、L2 およびパワー正規化されます。パワー正規化は、0 <= alpha <= 1 の場合、単に f(z) = sign(z) pow(abs(z), alpha) です。
- alphafloat, default=0.5
パワー正規化ステップのパラメータ。improved=False の場合は無視されます。
- 戻り値:
- fisher_vectornp.ndarray
計算されたフィッシャーベクトル。これは、パラメータ (混合重み、平均、および共分散行列) に関する GMM の勾配の連結によって与えられます。D 次元入力記述子またはベクトルの場合、K モード GMM では、フィッシャーベクトルの次元は 2KD + K になります。したがって、その次元は記述子/ベクトルの数に対して不変です。
参考文献
[1]Perronnin, F. and Dance, C. Fisher kernels on Visual Vocabularies for Image Categorization, IEEE Conference on Computer Vision and Pattern Recognition, 2007
[2]Perronnin, F. and Sanchez, J. and Mensink T. Improving the Fisher Kernel for Large-Scale Image Classification, ECCV, 2010
例
>>> from skimage.feature import fisher_vector, learn_gmm >>> sift_for_images = [np.random.random((10, 128)) for _ in range(10)] >>> num_modes = 16 >>> # Estimate 16-mode GMM with these synthetic SIFT vectors >>> gmm = learn_gmm(sift_for_images, n_modes=num_modes) >>> test_image_descriptors = np.random.random((25, 128)) >>> # Compute the Fisher vector >>> fv = fisher_vector(test_image_descriptors, gmm)
- skimage.feature.graycomatrix(image, distances, angles, levels=None, symmetric=False, normed=False)[ソース]#
グレースケール共起行列を計算します。
グレースケール共起行列は、画像上の指定されたオフセットでの共起するグレースケール値のヒストグラムです。
バージョン 0.19 で変更:
greymatrixは 0.19 でgraymatrixに名前が変更されました。- パラメータ:
- imagearray_like
整数型の入力画像。正の値の画像のみがサポートされています。型が uint8 以外の場合は、引数
levelsを設定する必要があります。- distancesarray_like
ピクセルペアの距離オフセットのリスト。
- anglesarray_like
ラジアン単位のピクセルペア角度のリスト。
- levelsint, optional
入力画像には、整数 [0,
levels-1] が含まれている必要があります。ここで、levels はカウントされたグレースケールレベルの数を示します (通常、8 ビット画像の場合は 256)。この引数は 16 ビット以上の画像で必須であり、通常は画像の最大値です。出力行列は少なくともlevelsxlevelsであるため、levelsに大きな値を使用するのではなく、入力画像のビニングを使用することをお勧めします。- symmetricbool, optional
True の場合、出力行列
P[:, :, d, theta]は対称になります。これは、値ペアの順序を無視することによって実現されるため、指定されたオフセットに対して (i, j) が検出されると、(i, j) と (j, i) の両方が累積されます。デフォルトは False です。- normedbool, optional
True の場合、与えられたオフセットに対して累積された共起の合計数で除算することにより、各行列
P[:, :, d, theta]を正規化します。結果の行列の要素は合計で 1 になります。デフォルトは False です。
- 戻り値:
- P4 次元 ndarray
グレースケール共起ヒストグラム。値
P[i,j,d,theta]は、グレースケールjが、グレースケールiから距離dおよび角度thetaで発生する回数です。normedがFalseの場合、出力は uint32 型で、それ以外の場合は float64 型です。次元は、レベル x レベル x 距離の数 x 角度の数です。
参考文献
[1]M. Hall-Beyer, 2007. GLCM Texture: A Tutorial https://prism.ucalgary.ca/handle/1880/51900 DOI:
10.11575/PRISM/33280[2]R.M. Haralick, K. Shanmugam, and I. Dinstein, “Textural features for image classification”, IEEE Transactions on Systems, Man, and Cybernetics, vol. SMC-3, no. 6, pp. 610-621, Nov. 1973. DOI:10.1109/TSMC.1973.4309314
[3]M. Nadler and E.P. Smith, Pattern Recognition Engineering, Wiley-Interscience, 1993.
[4]Wikipedia, https://en.wikipedia.org/wiki/Co-occurrence_matrix
例
1 ピクセルの距離と 4 つの異なる角度を使用して、4 つの GLCM を計算します。たとえば、0 ラジアンの角度は、右側の隣接ピクセルを指します。pi/4 ラジアンは、右上の対角隣接ピクセルを指します。pi/2 ラジアンは、上のピクセルを指します。以下同様です。
>>> image = np.array([[0, 0, 1, 1], ... [0, 0, 1, 1], ... [0, 2, 2, 2], ... [2, 2, 3, 3]], dtype=np.uint8) >>> result = graycomatrix(image, [1], [0, np.pi/4, np.pi/2, 3*np.pi/4], ... levels=4) >>> result[:, :, 0, 0] array([[2, 2, 1, 0], [0, 2, 0, 0], [0, 0, 3, 1], [0, 0, 0, 1]], dtype=uint32) >>> result[:, :, 0, 1] array([[1, 1, 3, 0], [0, 1, 1, 0], [0, 0, 0, 2], [0, 0, 0, 0]], dtype=uint32) >>> result[:, :, 0, 2] array([[3, 0, 2, 0], [0, 2, 2, 0], [0, 0, 1, 2], [0, 0, 0, 0]], dtype=uint32) >>> result[:, :, 0, 3] array([[2, 0, 0, 0], [1, 1, 2, 0], [0, 0, 2, 1], [0, 0, 0, 0]], dtype=uint32)
- skimage.feature.graycoprops(P, prop='contrast')[ソース]#
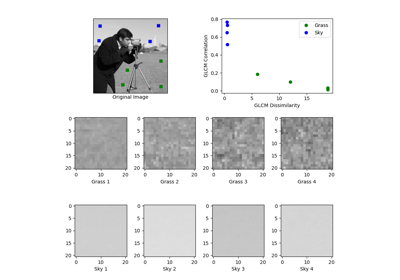
GLCMのテクスチャプロパティを計算します。
行列の簡潔な要約として機能するように、グレースケール共起行列の機能を計算します。プロパティは次のように計算されます
「コントラスト」: \(\sum_{i,j=0}^{levels-1} P_{i,j}(i-j)^2\)
「非類似度」: \(\sum_{i,j=0}^{levels-1}P_{i,j}|i-j|\)
「均質性」: \(\sum_{i,j=0}^{levels-1}\frac{P_{i,j}}{1+(i-j)^2}\)
「ASM」: \(\sum_{i,j=0}^{levels-1} P_{i,j}^2\)
「エネルギー」: \(\sqrt{ASM}\)
- 「相関」
- \[\sum_{i,j=0}^{levels-1} P_{i,j}\left[\frac{(i-\mu_i) \ (j-\mu_j)}{\sqrt{(\sigma_i^2)(\sigma_j^2)}}\right]\]
「平均」: \(\sum_{i=0}^{levels-1} i*P_{i}\)
「分散」: \(\sum_{i=0}^{levels-1} P_{i}*(i-mean)^2\)
‘std’: \(\sqrt{variance}\)
‘エントロピー’: \(\sum_{i,j=0}^{levels-1} -P_{i,j}*log(P_{i,j})\)
テクスチャ特性の計算前に、各GLCMは合計が1になるように正規化されます。
バージョン 0.19 で変更:
greycopropsは、0.19 でgraycopropsに名前が変更されました。- パラメータ:
- Pndarray
入力配列。
Pは、指定された特性を計算するグレースケール共起ヒストグラムです。値P[i,j,d,theta]は、グレースケール j がグレースケール i から距離 d、角度 theta で発生する回数です。- prop{‘contrast’, ‘dissimilarity’, ‘homogeneity’, ‘energy’, ‘correlation’, ‘ASM’, ‘mean’, ‘variance’, ‘std’, ‘entropy’}, オプション
計算するGLCMのプロパティ。デフォルトは ‘contrast’ です。
- 戻り値:
- results2次元 ndarray
2次元配列。
results[d, a]は、d番目の距離とa番目の角度に対するプロパティ ‘prop’ です。
参考文献
[1]M. Hall-Beyer, 2007. GLCM Texture: A Tutorial v. 1.0 through 3.0. The GLCM Tutorial Home Page, https://prism.ucalgary.ca/handle/1880/51900 DOI:
10.11575/PRISM/33280例
距離 [1, 2] と角度 [0度, 90度] のGLCMのコントラストを計算します
>>> image = np.array([[0, 0, 1, 1], ... [0, 0, 1, 1], ... [0, 2, 2, 2], ... [2, 2, 3, 3]], dtype=np.uint8) >>> g = graycomatrix(image, [1, 2], [0, np.pi/2], levels=4, ... normed=True, symmetric=True) >>> contrast = graycoprops(g, 'contrast') >>> contrast array([[0.58333333, 1. ], [1.25 , 2.75 ]])
- skimage.feature.haar_like_feature(int_image, r, c, width, height, feature_type=None, feature_coord=None)[ソース]#
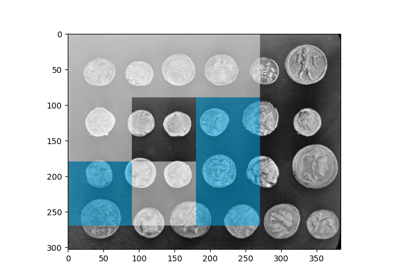
積分画像の関心領域(ROI)に対するHaar様特徴を計算します。
Haarライク特徴は、画像分類と物体検出に成功裏に使用されています [1]。 [2]で提案されたリアルタイム顔検出アルゴリズムに使用されています。
- パラメータ:
- int_image(M, N) ndarray
特徴を計算する必要がある積分画像。
- rint
検出ウィンドウの左上隅の行座標。
- cint
検出ウィンドウの左上隅の列座標。
- widthint
検出ウィンドウの幅。
- heightint
検出ウィンドウの高さ。
- feature_typestr または str のリストまたは None, オプション
考慮する特徴のタイプ
‘type-2-x’: x軸に沿って変化する2つの長方形;
‘type-2-y’: y軸に沿って変化する2つの長方形;
‘type-3-x’: x軸に沿って変化する3つの長方形;
‘type-3-y’: y軸に沿って変化する3つの長方形;
‘type-4’: x軸とy軸に沿って変化する4つの長方形。
デフォルトでは、すべての特徴が抽出されます。
feature_coordと共に使用する場合は、関連する各座標特徴の特徴タイプに対応する必要があります。- feature_coordタプルのリストまたはNoneのndarray, optional
抽出する座標の配列。これは、機能のサブセットのみを再計算する場合に役立ちます。この場合、
feature_typeは、haar_like_feature_coord()によって返されるように、各機能のタイプを含む配列である必要があります。デフォルトでは、すべての座標が計算されます。
- 戻り値:
注釈
これらの特徴を並列で抽出する場合は、バックエンドの選択(マルチプロセッシング対スレッド化)がパフォーマンスに影響を与えることに注意してください。経験則は次のとおりです。画像内の可能なすべてのROIの特徴を抽出する場合はマルチプロセッシングを使用します。限られた数のROIの特定の場所で特徴を抽出する場合はスレッド化を使用します。詳細については、例の Haarライク特徴記述子を使用した顔分類を参照してください。
参考文献
[2]Oren, M., Papageorgiou, C., Sinha, P., Osuna, E., & Poggio, T. (1997, June). Pedestrian detection using wavelet templates. In Computer Vision and Pattern Recognition, 1997. Proceedings., 1997 IEEE Computer Society Conference on (pp. 193-199). IEEE. http://tinyurl.com/y6ulxfta DOI:10.1109/CVPR.1997.609319
[3]Viola, Paul, and Michael J. Jones. “Robust real-time face detection.” International journal of computer vision 57.2 (2004): 137-154. https://www.merl.com/publications/docs/TR2004-043.pdf DOI:10.1109/CVPR.2001.990517
例
>>> import numpy as np >>> from skimage.transform import integral_image >>> from skimage.feature import haar_like_feature >>> img = np.ones((5, 5), dtype=np.uint8) >>> img_ii = integral_image(img) >>> feature = haar_like_feature(img_ii, 0, 0, 5, 5, 'type-3-x') >>> feature array([-1, -2, -3, -4, -5, -1, -2, -3, -4, -5, -1, -2, -3, -4, -5, -1, -2, -3, -4, -1, -2, -3, -4, -1, -2, -3, -4, -1, -2, -3, -1, -2, -3, -1, -2, -3, -1, -2, -1, -2, -1, -2, -1, -1, -1])
事前に計算された座標の機能も計算できます。
>>> from skimage.feature import haar_like_feature_coord >>> feature_coord, feature_type = zip( ... *[haar_like_feature_coord(5, 5, feat_t) ... for feat_t in ('type-2-x', 'type-3-x')]) >>> # only select one feature over two >>> feature_coord = np.concatenate([x[::2] for x in feature_coord]) >>> feature_type = np.concatenate([x[::2] for x in feature_type]) >>> feature = haar_like_feature(img_ii, 0, 0, 5, 5, ... feature_type=feature_type, ... feature_coord=feature_coord) >>> feature array([ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, -3, -5, -2, -4, -1, -3, -5, -2, -4, -2, -4, -2, -4, -2, -1, -3, -2, -1, -1, -1, -1, -1])
- skimage.feature.haar_like_feature_coord(width, height, feature_type=None)[ソース]#
Haar様特徴の座標を計算します。
- パラメータ:
- widthint
検出ウィンドウの幅。
- heightint
検出ウィンドウの高さ。
- feature_typestr または str のリストまたは None, オプション
考慮する特徴のタイプ
‘type-2-x’: x軸に沿って変化する2つの長方形;
‘type-2-y’: y軸に沿って変化する2つの長方形;
‘type-3-x’: x軸に沿って変化する3つの長方形;
‘type-3-y’: y軸に沿って変化する3つの長方形;
‘type-4’: x軸とy軸に沿って変化する4つの長方形。
デフォルトでは、すべての特徴が抽出されます。
- 戻り値:
- feature_coord(n_features, n_rectangles, 2, 2), ndarray of list of tuple coord
各特徴の長方形の座標。
- feature_type(n_features,), str のndarray
各特徴に対応するタイプ。
例
>>> import numpy as np >>> from skimage.transform import integral_image >>> from skimage.feature import haar_like_feature_coord >>> feat_coord, feat_type = haar_like_feature_coord(2, 2, 'type-4') >>> feat_coord array([ list([[(0, 0), (0, 0)], [(0, 1), (0, 1)], [(1, 1), (1, 1)], [(1, 0), (1, 0)]])], dtype=object) >>> feat_type array(['type-4'], dtype=object)
- skimage.feature.hessian_matrix(image, sigma=1, mode='constant', cval=0, order='rc', use_gaussian_derivatives=None)[ソース]#
ヘッセ行列を計算します。
2Dでは、ヘッセ行列は次のように定義されます
H = [Hrr Hrc] [Hrc Hcc]
これは、それぞれのr方向およびc方向のガウスカーネルの2次微分で画像を畳み込むことによって計算されます。
ここでの実装は、n次元データもサポートしています。
- パラメータ:
- imagendarray
入力画像。
- sigmafloat
自己相関行列の重み関数として使用されるガウシアンカーネルに使用される標準偏差。
- mode{‘constant’, ‘reflect’, ‘wrap’, ‘nearest’, ‘mirror’}, optional
画像の境界外の値を処理する方法。
- cvalfloat, optional
mode 'constant' と組み合わせて使用される、画像の境界外の値。
- order{‘rc’, ‘xy’}, オプション
2D画像の場合、このパラメーターを使用すると、勾配計算で画像軸の逆順または正順を使用できます。 ‘rc’ は、最初の軸を最初に使用することを示し(Hrr、Hrc、Hcc)、 ‘xy’ は、最後の軸を最初に使用することを示します(Hxx、Hxy、Hyy)。より高次元の画像では、常に ‘rc’ の順序を使用する必要があります。
- use_gaussian_derivativesboolean, オプション
ヘッセ行列をガウス微分で畳み込むか、単純な有限差分演算で計算するかを示します。
- 戻り値:
- H_elemsndarray のリスト
入力画像の各ピクセルに対するヘッセ行列の上三角要素。2Dでは、[Hrr、Hrc、Hcc] を含む3つの要素のリストになります。nDでは、リストには
(n**2 + n) / 2個の配列が含まれます。
注釈
微分と畳み込みの分配性により、ガウスカーネルGで平滑化された画像Iの微分は、画像のGの微分との畳み込みとして言い換えることができます。
\[\frac{\partial }{\partial x_i}(I * G) = I * \left( \frac{\partial }{\partial x_i} G \right)\]use_gaussian_derivativesがTrueの場合、このプロパティを使用して、ヘッセ行列を構成する2次微分を計算します。use_gaussian_derivativesがFalseの場合、代わりにガウス平滑化画像での単純な有限差分が使用されます。例
>>> from skimage.feature import hessian_matrix >>> square = np.zeros((5, 5)) >>> square[2, 2] = 4 >>> Hrr, Hrc, Hcc = hessian_matrix(square, sigma=0.1, order='rc', ... use_gaussian_derivatives=False) >>> Hrc array([[ 0., 0., 0., 0., 0.], [ 0., 1., 0., -1., 0.], [ 0., 0., 0., 0., 0.], [ 0., -1., 0., 1., 0.], [ 0., 0., 0., 0., 0.]])
- skimage.feature.hessian_matrix_det(image, sigma=1, approximate=True)[ソース]#
画像全体の近似ヘッセ行列式を計算します。
2D近似法では、積分画像上のボックスフィルターを使用して、おおよそのヘッセ行列式を計算します。
- パラメータ:
- imagendarray
ヘッセ行列式を計算する画像。
- sigmafloat, optional
ヘッセ行列に使用されるガウスカーネルの標準偏差。
- approximatebool, オプション
Trueで、画像が 2D の場合は、はるかに高速な近似計算を使用します。この引数は、3D以上の画像には影響しません。
- 戻り値:
- out配列
ヘッセ行列式の配列。
注釈
2D画像の場合、
approximate=Trueの場合、このメソッドの実行時間は画像のサイズのみに依存します。予想どおり、sigmaには依存しません。欠点は、sigmaが3未満の結果が正確でない、つまり、ヘッセ行列を計算してその行列式をとった場合に得られる結果と類似していないことです。参考文献
[1]Herbert Bay, Andreas Ess, Tinne Tuytelaars, Luc Van Gool, “SURF: Speeded Up Robust Features” ftp://ftp.vision.ee.ethz.ch/publications/articles/eth_biwi_00517.pdf
- skimage.feature.hessian_matrix_eigvals(H_elems)[ソース]#
ヘッセ行列の固有値を計算します。
- パラメータ:
- H_elemsndarray のリスト
hessian_matrixによって返されるヘッセ行列の上三角要素。
- 戻り値:
- eigsndarray
ヘッセ行列の固有値を降順に並べたものです。固有値が主次元です。つまり、
eigs[i, j, k]は、位置 (j, k) における i 番目に大きい固有値を格納します。
例
>>> from skimage.feature import hessian_matrix, hessian_matrix_eigvals >>> square = np.zeros((5, 5)) >>> square[2, 2] = 4 >>> H_elems = hessian_matrix(square, sigma=0.1, order='rc', ... use_gaussian_derivatives=False) >>> hessian_matrix_eigvals(H_elems)[0] array([[ 0., 0., 2., 0., 0.], [ 0., 1., 0., 1., 0.], [ 2., 0., -2., 0., 2.], [ 0., 1., 0., 1., 0.], [ 0., 0., 2., 0., 0.]])
- skimage.feature.hog(image, orientations=9, pixels_per_cell=(8, 8), cells_per_block=(3, 3), block_norm='L2-Hys', visualize=False, transform_sqrt=False, feature_vector=True, *, channel_axis=None)[source]#
与えられた画像に対して、方向勾配のヒストグラム(HOG)を抽出します。
次の手順で、方向勾配ヒストグラム (HOG) を計算します。
(オプション) グローバルな画像正規化
rowとcolにおける勾配画像を計算勾配ヒストグラムの計算
ブロック間の正規化
特徴ベクトルへの平坦化
- パラメータ:
- image(M, N[, C]) ndarray
入力画像。
- orientationsint, optional
方向ビンの数。
- pixels_per_cell2-タプル (int, int), オプション
セルのサイズ (ピクセル単位)。
- cells_per_block2-タプル (int, int), オプション
各ブロック内のセル数。
- block_normstr {‘L1’, ‘L1-sqrt’, ‘L2’, ‘L2-Hys’}, オプション
ブロック正規化法
- visualizebool, optional
HOG 画像も返します。各セルと方向ビンについて、画像には、セルの中央に位置し、方向ビンが及ぶ角度範囲の中点に垂直で、対応するヒストグラム値に比例する強度を持つ線分が含まれます。
- transform_sqrtbool, オプション
処理前に画像正規化のためにべき乗則圧縮を適用します。画像に負の値が含まれる場合は使用しないでください。以下の
notesセクションも参照してください。- feature_vectorbool, オプション
返す直前に結果に .ravel() を呼び出すことで、データを特徴ベクトルとして返します。
- channel_axisint または None, オプション
None の場合、画像はグレースケール (シングルチャンネル) 画像であると想定されます。それ以外の場合、このパラメーターは、配列のどの軸がチャンネルに対応するかを示します。
バージョン 0.19 で追加:
channel_axisは 0.19 で追加されました。
- 戻り値:
- out(n_blocks_row, n_blocks_col, n_cells_row, n_cells_col, n_orient) ndarray
画像の HOG 記述子。
feature_vectorが True の場合は、1D (平坦化された) 配列が返されます。- hog_image(M, N) ndarray, optional
HOG 画像の可視化。
visualizeが True の場合にのみ提供されます。
- 例外発生:
- ValueError
pixels_per_cell と cells_per_block の値が与えられた場合、画像が小さすぎる場合。
注釈
提示されたコードは、[2] の HOG 抽出法を以下の変更を加えて実装しています。(I) (3, 3) セルのブロックを使用 (論文では (2, 2))。(II) セル内での平滑化なし (論文では sigma=8 ピクセルのガウス空間ウィンドウ)。(III) L1 ブロック正規化を使用 (論文では L2-Hys)。
ガンマ補正としても知られるべき乗則圧縮は、影と照明の変化の影響を軽減するために使用されます。圧縮によって、暗い領域が明るくなります。キーワード引数
transform_sqrtがTrueに設定されている場合、関数は各カラーチャンネルの平方根を計算し、次に画像に hog アルゴリズムを適用します。参考文献
[2]Dalal, N and Triggs, B, Histograms of Oriented Gradients for Human Detection, IEEE Computer Society Conference on Computer Vision and Pattern Recognition 2005 San Diego, CA, USA, https://lear.inrialpes.fr/people/triggs/pubs/Dalal-cvpr05.pdf, DOI:10.1109/CVPR.2005.177
[3]Lowe, D.G., Distinctive image features from scale-invatiant keypoints, International Journal of Computer Vision (2004) 60: 91, http://www.cs.ubc.ca/~lowe/papers/ijcv04.pdf, DOI:10.1023/B:VISI.0000029664.99615.94
[4]Dalal, N, Finding People in Images and Videos, Human-Computer Interaction [cs.HC], Institut National Polytechnique de Grenoble - INPG, 2006, https://tel.archives-ouvertes.fr/tel-00390303/file/NavneetDalalThesis.pdf
- skimage.feature.learn_gmm(descriptors, *, n_modes=32, gm_args=None)[source]#
記述子とモード数 (つまりガウス分布) のセットが与えられた場合に、ガウス混合モデル (GMM) を推定します。この関数は、本質的には、scikit-learn の GMM の実装、つまり にある
sklearn.mixture.GaussianMixtureクラスのラッパーです。フィッシャーベクトルの性質上、基となる scikit-learn クラスの強制パラメータは、'diag' でなければならない covariance_type のみです。
n_modesに使用する値を事前に知る簡単な方法はありません。通常、値は{16, 32, 64, 128}のいずれかです。いくつかの GMM をトレーニングし、GMM の対数確率を最大化するものを選択するか、結果として得られるフィッシャーベクトルでトレーニングされたダウンストリーム分類器が最大のパフォーマンスを発揮するようにn_modesを選択することができます。- パラメータ:
- descriptorsnp.ndarray (N, M) または list [(N1, M), (N2, M), …]
GMM の推定に使用される記述子の NumPy 配列のリスト、または単一の NumPy 配列。NumPy 配列のリストが許可されている理由は、フィッシャーベクトルのエンコードを使用する場合、記述子/ベクトルは、データセット内の各サンプル/画像 (たとえば、各画像の SIFT ベクトル) に対して個別に計算されることが多いためです。リストが渡された場合、各要素は、行数が異なる可能性がある (たとえば、各画像で SIFT ベクトルの数が異なる) NumPy 配列である必要がありますが、各列の数は同じである必要があります (つまり、次元が同じである必要があります)。
- n_modesint
GMM 推定中に推定するモード/ガウス分布の数。
- gm_argsdict
基となる scikit-learn にある
sklearn.mixture.GaussianMixtureクラスに渡すことができるキーワード引数。
- 戻り値:
- gmm
sklearn.mixture.GaussianMixture フィッシャーベクトルの計算に必要なパラメータを含む、推定された GMM オブジェクト。
- gmm
参考文献
例
>>> from skimage.feature import fisher_vector >>> rng = np.random.Generator(np.random.PCG64()) >>> sift_for_images = [rng.standard_normal((10, 128)) for _ in range(10)] >>> num_modes = 16 >>> # Estimate 16-mode GMM with these synthetic SIFT vectors >>> gmm = learn_gmm(sift_for_images, n_modes=num_modes)
- skimage.feature.local_binary_pattern(image, P, R, method='default')[source]#
画像のローカルバイナリパターン(LBP)を計算します。
LBP は、テクスチャ分類でよく使用される視覚記述子です。
- パラメータ:
- image(M, N) array
2D グレースケール画像。
- Pint
円対称の隣接点セットのポイント数 (角度空間の量子化)。
- Rfloat
円の半径 (演算子の空間分解能)。
- methodstr {‘default’, ‘ror’, ‘uniform’, ‘nri_uniform’, ‘var’}, オプション
パターンを決定する方法
- 戻り値:
- 出力(M, N) 配列
LBP画像。
参考文献
[1]T. Ojala, M. Pietikainen, T. Maenpaa, “Multiresolution gray-scale and rotation invariant texture classification with local binary patterns”, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 24, no. 7, pp. 971-987, July 2002 DOI:10.1109/TPAMI.2002.1017623
[2]T. Ahonen, A. Hadid and M. Pietikainen. “Face recognition with local binary patterns”, in Proc. Eighth European Conf. Computer Vision, Prague, Czech Republic, May 11-14, 2004, pp. 469-481, 2004. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.214.6851 DOI:10.1007/978-3-540-24670-1_36
[3]T. Ahonen, A. Hadid and M. Pietikainen, “Face Description with Local Binary Patterns: Application to Face Recognition”, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 28, no. 12, pp. 2037-2041, Dec. 2006 DOI:10.1109/TPAMI.2006.244
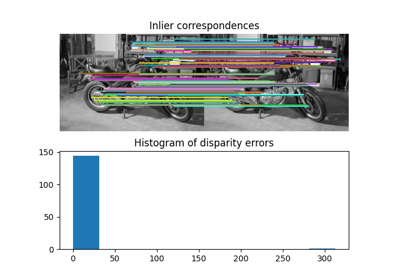
- skimage.feature.match_descriptors(descriptors1, descriptors2, metric=None, p=2, max_distance=inf, cross_check=True, max_ratio=1.0)[ソース]#
記述子のブルートフォースマッチング。
このマッチャーは、最初のセットの各記述子について、2番目のセットで最も近い記述子を見つけます(クロスチェックが有効な場合は逆も同様)。
- パラメータ:
- descriptors1(M, P) 配列
最初の画像のM個のキーポイントに関するサイズPの記述子。
- descriptors2(N, P) 配列
2番目の画像のN個のキーポイントに関するサイズPの記述子。
- metric{'euclidean', 'cityblock', 'minkowski', 'hamming', …}, オプション
2つの記述子間の距離を計算するためのメトリック。
scipy.spatial.distance.cdistですべての可能なタイプを参照してください。ハミング距離はバイナリ記述子に使用する必要があります。デフォルトでは、L2ノルムはfloatまたはdouble型のすべての記述子に使用され、ハミング距離はバイナリ記述子に自動的に使用されます。- pint, オプション
metric='minkowski'に適用するpノルム。- max_distancefloat, オプション
別々の画像の2つのキーポイントの記述子間の、マッチとみなされる最大許容距離。
- cross_checkbool, オプション
Trueの場合、マッチしたキーポイントは、クロスチェック後に返されます。つまり、キーポイント2が2番目の画像でキーポイント1に最適なマッチであり、キーポイント1が最初の画像でキーポイント2に最適なマッチである場合に、マッチしたペア(キーポイント1、キーポイント2)が返されます。
- max_ratiofloat, オプション
2番目の記述子セットでの、最初の最も近い記述子と2番目に最も近い記述子間の距離の最大比率。この閾値は、2つの記述子セット間の曖昧なマッチをフィルタリングするのに役立ちます。この値の選択は、選択した記述子の統計に依存します。たとえば、SIFT記述子の場合は、通常0.8の値が選択されます。D.G. Lowe, “Distinctive Image Features from Scale-Invariant Keypoints”, International Journal of Computer Vision, 2004 を参照してください。
- 戻り値:
- matches(Q, 2) 配列
最初と2番目の記述子セット内の対応するマッチのインデックス。ここで、
matches[:, 0]は最初のインデックスを表し、matches[:, 1]は2番目の記述子セットのインデックスを表します。
- skimage.feature.match_template(image, template, pad_input=False, mode='constant', constant_values=0)[ソース]#
正規化相関を使用して、テンプレートを2Dまたは3D画像にマッチングします。
出力は、-1.0〜1.0の値を持つ配列です。指定された位置の値は、画像とテンプレート間の相関係数に対応します。
pad_input=Trueの場合、マッチはテンプレートの中心に対応し、それ以外の場合はテンプレートの左上隅に対応します。最適なマッチを見つけるには、応答(出力)画像でピークを探す必要があります。- パラメータ:
- image(M, N[, P]) 配列
2Dまたは3Dの入力画像。
- template(m, n[, p]) 配列
配置するテンプレート。
(m <= M, n <= N[, p <= P])である必要があります。- pad_inputbool
Trueの場合、
imageをパディングして、出力が画像と同じサイズになり、出力値がテンプレートの中心に対応するようにします。それ以外の場合、出力は、(M, N)画像と(m, n)テンプレートの場合、形状が(M - m + 1, N - n + 1)の配列になり、マッチはテンプレートの原点(左上隅)に対応します。- mode
numpy.padを参照、オプション パディングモード。
- constant_values
numpy.padを参照、オプション mode='constant'と組み合わせて使用される定数値。
- 戻り値:
- output配列
相関係数を持つ応答画像。
注釈
相互相関の詳細については、[1] で説明しています。この実装では、画像とテンプレートのFFT畳み込みを使用します。[2] は同様の導出を示していますが、この参照で示されている近似はこの実装では使用されていません。
参考文献
[1]J. P. Lewis, “Fast Normalized Cross-Correlation”, Industrial Light and Magic.
[2]Briechle and Hanebeck, “Template Matching using Fast Normalized Cross Correlation”, Proceedings of the SPIE (2001). DOI:10.1117/12.421129
例
>>> template = np.zeros((3, 3)) >>> template[1, 1] = 1 >>> template array([[0., 0., 0.], [0., 1., 0.], [0., 0., 0.]]) >>> image = np.zeros((6, 6)) >>> image[1, 1] = 1 >>> image[4, 4] = -1 >>> image array([[ 0., 0., 0., 0., 0., 0.], [ 0., 1., 0., 0., 0., 0.], [ 0., 0., 0., 0., 0., 0.], [ 0., 0., 0., 0., 0., 0.], [ 0., 0., 0., 0., -1., 0.], [ 0., 0., 0., 0., 0., 0.]]) >>> result = match_template(image, template) >>> np.round(result, 3) array([[ 1. , -0.125, 0. , 0. ], [-0.125, -0.125, 0. , 0. ], [ 0. , 0. , 0.125, 0.125], [ 0. , 0. , 0.125, -1. ]]) >>> result = match_template(image, template, pad_input=True) >>> np.round(result, 3) array([[-0.125, -0.125, -0.125, 0. , 0. , 0. ], [-0.125, 1. , -0.125, 0. , 0. , 0. ], [-0.125, -0.125, -0.125, 0. , 0. , 0. ], [ 0. , 0. , 0. , 0.125, 0.125, 0.125], [ 0. , 0. , 0. , 0.125, -1. , 0.125], [ 0. , 0. , 0. , 0.125, 0.125, 0.125]])
- skimage.feature.multiblock_lbp(int_image, r, c, width, height)[ソース]#
マルチブロックローカルバイナリパターン(MB-LBP)。
この特徴は、ローカルバイナリパターン(LBP)(
local_binary_pattern()を参照)と同様に計算されますが、個々のピクセル値の代わりに合計ブロックが使用される点が異なります。MB-LBPは、積分画像を使用して一定時間で複数のスケールで計算できるLBPの拡張版です。特徴量を計算するために、均等なサイズの9つの長方形が使用されます。各長方形について、ピクセル強度の合計が計算されます。これらの合計と中央の長方形の合計との比較によって、LBPと同様に特徴量が決定されます。
- パラメータ:
- int_image(N, M) 配列
積分画像。
- rint
特徴量を含む長方形の左上隅の行座標。
- cint
特徴量を含む長方形の左上隅の列座標。
- widthint
特徴量の計算に使用される9つの等しい長方形のうちの1つの幅。
- heightint
特徴量の計算に使用される9つの等しい長方形のうちの1つの高さ。
- 戻り値:
- 出力int
8ビットMB-LBP特徴記述子。
参考文献
[1]L. Zhang, R. Chu, S. Xiang, S. Liao, S.Z. Li. “Face Detection Based on Multi-Block LBP Representation”, In Proceedings: Advances in Biometrics, International Conference, ICB 2007, Seoul, Korea. http://www.cbsr.ia.ac.cn/users/scliao/papers/Zhang-ICB07-MBLBP.pdf DOI:10.1007/978-3-540-74549-5_2
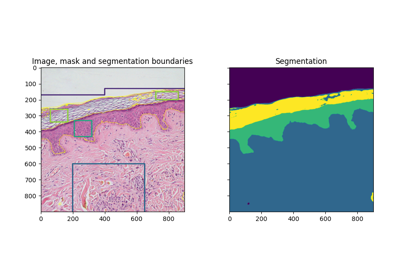
- skimage.feature.multiscale_basic_features(image, intensity=True, edges=True, texture=True, sigma_min=0.5, sigma_max=16, num_sigma=None, num_workers=None, *, channel_axis=None)[ソース]#
単一または多チャネルのnd画像用のローカル特徴。
強度、勾配強度、および局所構造は、ガウシアンブラー処理によって異なるスケールで計算されます。
- パラメータ:
- imagendarray
グレースケールまたはマルチチャネルが可能な入力画像。
- intensitybool, デフォルト True
Trueの場合、異なるスケールで平均化されたピクセル強度が特徴セットに追加されます。
- edgesbool, デフォルト True
Trueの場合、異なるスケールで平均化された局所勾配の強度が特徴セットに追加されます。
- texturebool, デフォルト True
Trueの場合、異なるスケールでガウシアンブラー処理後のヘッセ行列の固有値が特徴セットに追加されます。
- sigma_minfloat, オプション
特徴量を抽出する前に局所近傍を平均化するために使用されるガウスカーネルの最小値。
- sigma_maxfloat, オプション
特徴量を抽出する前に局所近傍を平均化するために使用されるガウスカーネルの最大値。
- num_sigmaint, optional
sigma_minとsigma_maxの間のガウスカーネルの値の数。Noneの場合、sigma_minに2の累乗を掛けた値が使用されます。
- num_workersint または None, オプション
使用する並列スレッドの数。
Noneに設定すると、利用可能なすべてのコアが使用されます。- channel_axisint または None, オプション
None の場合、画像はグレースケール (シングルチャンネル) 画像であると想定されます。それ以外の場合、このパラメーターは、配列のどの軸がチャンネルに対応するかを示します。
バージョン 0.19 で追加:
channel_axisは 0.19 で追加されました。
- 戻り値:
- featuresnp.ndarray
形状
image.shape + (n_features,)の配列。channel_axisが None でない場合、すべてのチャネルは特徴次元に沿って連結されます(つまり、n_features == n_features_singlechannel * n_channels)。
- skimage.feature.peak_local_max(image, min_distance=1, threshold_abs=None, threshold_rel=None, exclude_border=True, num_peaks=inf, footprint=None, labels=None, num_peaks_per_label=inf, p_norm=inf)[ソース]#
画像内のピークを座標リストとして検出します。
ピークは、
2 * min_distance + 1の領域内の局所最大値です(つまり、ピークは少なくともmin_distanceで区切られています)。threshold_absとthreshold_relの両方が指定されている場合、2つの最大値がピークの最小強度しきい値として選択されます。バージョン 0.18 で変更: バージョン 0.18 より前は、
min_distanceの半径内の同じ高さのピークがすべて返されていましたが、これにより予期しない動作が発生する可能性がありました。0.18以降、領域内の任意のピークが返されます。問題 gh-2592 を参照してください。- パラメータ:
- imagendarray
入力画像。
- min_distanceint, optional
ピークを分離する最小許容距離。ピークの最大数を見つけるには、
min_distance=1を使用します。- threshold_absfloat または None, オプション
ピークの最小強度。デフォルトでは、絶対しきい値は画像の最小強度です。
- threshold_relfloatまたはNone、オプション
ピークの最小強度。
max(image) * threshold_relとして計算されます。- exclude_borderint, int のタプル, または bool, オプション
正の整数の場合、
exclude_borderは、画像の境界からexclude_borderピクセル以内のピークを除外します。非負の整数のタプルの場合、タプルの長さは入力配列の次元数と一致する必要があります。タプルの各要素は、その次元に沿って画像の境界からexclude_borderピクセル以内のピークを除外します。Trueの場合、min_distanceパラメータを値として取ります。ゼロまたはFalseの場合、ピークは境界からの距離に関係なく識別されます。- num_peaksint, オプション
ピークの最大数。ピークの数が
num_peaksを超える場合、ピーク強度が最も高いnum_peaks個のピークを返します。- footprintbool の ndarray, オプション
指定した場合、
footprint == 1は、image内のすべての点でピークを検索するローカル領域を表します。- labelsint の ndarray, オプション
指定した場合、各一意の領域
labels == valueは、ピークを検索する一意の領域を表します。ゼロは背景用に予約されています。- num_peaks_per_labelint, オプション
ラベルごとのピークの最大数。
- p_normfloat
使用するミンコフスキーpノルム。範囲[1, inf]である必要があります。オーバーフローが発生する可能性がある場合、有限の大きなpはValueErrorを引き起こす可能性があります。
infはチェビシェフ距離に対応し、2はユークリッド距離に対応します。
- 戻り値:
- 出力ndarray
ピークの座標。
注釈
ピークローカル最大値関数は、画像内のローカルピーク(最大値)の座標を返します。内部では、最大値フィルターがローカル最大値を検索するために使用されます。この操作により、元の画像が拡張されます。拡張された画像と元の画像を比較した後、この関数は、拡張された画像が元の画像と等しいピークの座標を返します。
例
>>> img1 = np.zeros((7, 7)) >>> img1[3, 4] = 1 >>> img1[3, 2] = 1.5 >>> img1 array([[0. , 0. , 0. , 0. , 0. , 0. , 0. ], [0. , 0. , 0. , 0. , 0. , 0. , 0. ], [0. , 0. , 0. , 0. , 0. , 0. , 0. ], [0. , 0. , 1.5, 0. , 1. , 0. , 0. ], [0. , 0. , 0. , 0. , 0. , 0. , 0. ], [0. , 0. , 0. , 0. , 0. , 0. , 0. ], [0. , 0. , 0. , 0. , 0. , 0. , 0. ]])
>>> peak_local_max(img1, min_distance=1) array([[3, 2], [3, 4]])
>>> peak_local_max(img1, min_distance=2) array([[3, 2]])
>>> img2 = np.zeros((20, 20, 20)) >>> img2[10, 10, 10] = 1 >>> img2[15, 15, 15] = 1 >>> peak_idx = peak_local_max(img2, exclude_border=0) >>> peak_idx array([[10, 10, 10], [15, 15, 15]])
>>> peak_mask = np.zeros_like(img2, dtype=bool) >>> peak_mask[tuple(peak_idx.T)] = True >>> np.argwhere(peak_mask) array([[10, 10, 10], [15, 15, 15]])
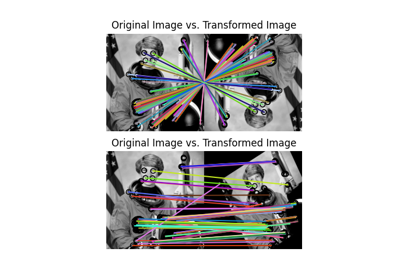
- skimage.feature.plot_matched_features(image0, image1, *, keypoints0, keypoints1, matches, ax, keypoints_color='k', matches_color=None, only_matches=False, alignment='horizontal')[ソース]#
2つの画像間のマッチした特徴をプロットします。
バージョン 0.23 で追加。
- パラメータ:
- image0(N, M [, 3]) 配列
最初の画像。
- image1(N, M [, 3]) 配列
2番目の画像。
- keypoints0(K1, 2) 配列
最初のキーポイント座標
(row, col)。- keypoints1(K2, 2) 配列
2番目のキーポイント座標
(row, col)。- matches(Q, 2) 配列
最初と2番目の記述子セットにおける対応するマッチのインデックス。ここで、
matches[:, 0](またはmatches[:, 1]) は、最初 (または 2 番目) の記述子セットのインデックスを含みます。- axmatplotlib.axes.Axes
画像とそれらのマッチした特徴が描画される Axes オブジェクト。
- keypoints_colormatplotlib の色、オプション
キーポイントの位置の色。
- matches_colormatplotlib の色またはそのシーケンス、オプション
matchesによって定義された各線に対する単一の色または色のシーケンス。これはキーポイントのマッチを接続します。サポートされている色の形式の概要については、[1] を参照してください。デフォルトでは、色はランダムに選択されます。- only_matchesbool, オプション
True に設定すると、キーポイントの位置ではなく、マッチのみをプロットします。
- alignment{‘horizontal’, ‘vertical’}, オプション
2つの画像を並べて表示する (
'horizontal') か、1つをもう1つの上に表示する ('vertical') か。
注釈
matches_colorに渡される色のシーケンスが任意の数のmatchesで機能するようにするには、そのシーケンスをitertools.cycle()でラップできます。参考文献
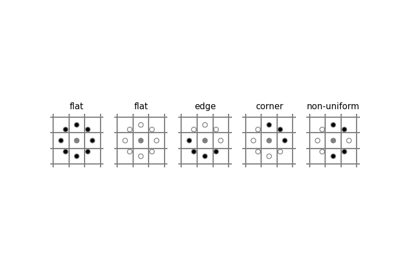
- skimage.feature.shape_index(image, sigma=1, mode='constant', cval=0)[ソース]#
形状インデックスを計算します。
Koenderink & van Doorn [1] によって定義された形状インデックスは、画像を高さを表す強度を持つ3D平面と仮定した場合の、局所的な曲率の単一値の尺度です。
これはヘッセ行列の固有値から導出され、その値は-1から1の範囲です (平坦な領域では未定義 (=NaN))。以下の範囲は以下の形状を表します。
形状インデックスの範囲と対応する形状。# 間隔 (s は ... に)
形状
[ -1, -7/8)
球形のカップ
[-7/8, -5/8)
スルー
[-5/8, -3/8)
溝
[-3/8, -1/8)
鞍形の溝
[-1/8, +1/8)
鞍
[+1/8, +3/8)
鞍形の尾根
[+3/8, +5/8)
尾根
[+5/8, +7/8)
ドーム
[+7/8, +1]
球形のキャップ
- パラメータ:
- image(M, N) ndarray
入力画像。
- sigmafloat, optional
ガウスカーネルに使用される標準偏差。これは、ヘッセ行列の固有値計算の前に、入力データを平滑化するために使用されます。
- mode{‘constant’, ‘reflect’, ‘wrap’, ‘nearest’, ‘mirror’}, optional
画像境界外の値を処理する方法
- cvalfloat, optional
mode 'constant' と組み合わせて使用される、画像の境界外の値。
- 戻り値:
- sndarray
形状インデックス
参考文献
[1]Koenderink, J. J. & van Doorn, A. J., “Surface shape and curvature scales”, Image and Vision Computing, 1992, 10, 557-564. DOI:10.1016/0262-8856(92)90076-F
例
>>> from skimage.feature import shape_index >>> square = np.zeros((5, 5)) >>> square[2, 2] = 4 >>> s = shape_index(square, sigma=0.1) >>> s array([[ nan, nan, -0.5, nan, nan], [ nan, -0. , nan, -0. , nan], [-0.5, nan, -1. , nan, -0.5], [ nan, -0. , nan, -0. , nan], [ nan, nan, -0.5, nan, nan]])
- skimage.feature.structure_tensor(image, sigma=1, mode='constant', cval=0, order='rc')[ソース]#
2乗差の合計を使用して構造テンソルを計算します。
(2次元) 構造テンソル A は次のように定義されます。
A = [Arr Arc] [Arc Acc]
これは、画像の各ピクセル周辺のローカルウィンドウでの2乗差の重み付き合計によって近似されます。この式は、より多くの次元に拡張できます ( [1] を参照)。
- パラメータ:
- imagendarray
入力画像。
- sigmafloat または float の配列のようなもの, オプション
ガウスカーネルに使用される標準偏差。これは、2乗差の局所的な合計の重み関数として使用されます。sigma が iterable の場合、その長さは
image.ndimと等しくなければならず、各要素はそれぞれの軸に適用されるガウスカーネルに使用されます。- mode{‘constant’, ‘reflect’, ‘wrap’, ‘nearest’, ‘mirror’}, optional
画像の境界外の値を処理する方法。
- cvalfloat, optional
mode 'constant' と組み合わせて使用される、画像の境界外の値。
- order{‘rc’, ‘xy’}, オプション
注:'xy'は 2D 画像のみのオプションであり、より高い次元では常に 'rc' 順序を使用する必要があります。このパラメータを使用すると、勾配計算で画像軸の逆順または順方向の順序を使用できます。'rc' は最初に最初の軸 (Arr, Arc, Acc) を使用することを示し、'xy' は最初に最後の軸 (Axx, Axy, Ayy) を使用することを示します。
- 戻り値:
- A_elemsndarray のリスト
入力画像の各ピクセルに対する構造テンソルの上三角要素。
参考文献
例
>>> from skimage.feature import structure_tensor >>> square = np.zeros((5, 5)) >>> square[2, 2] = 1 >>> Arr, Arc, Acc = structure_tensor(square, sigma=0.1, order='rc') >>> Acc array([[0., 0., 0., 0., 0.], [0., 1., 0., 1., 0.], [0., 4., 0., 4., 0.], [0., 1., 0., 1., 0.], [0., 0., 0., 0., 0.]])
- skimage.feature.structure_tensor_eigenvalues(A_elems)[ソース]#
構造テンソルの固有値を計算します。
- パラメータ:
- A_elemsndarray のリスト
structure_tensorによって返された、構造テンソルの上三角要素。
- 戻り値:
- ndarray
構造テンソルの固有値。降順で並べられます。固有値が先頭の次元です。つまり、座標 [i, j, k] は、位置 (j, k) における i 番目に大きい固有値に対応します。
例
>>> from skimage.feature import structure_tensor >>> from skimage.feature import structure_tensor_eigenvalues >>> square = np.zeros((5, 5)) >>> square[2, 2] = 1 >>> A_elems = structure_tensor(square, sigma=0.1, order='rc') >>> structure_tensor_eigenvalues(A_elems)[0] array([[0., 0., 0., 0., 0.], [0., 2., 4., 2., 0.], [0., 4., 0., 4., 0.], [0., 2., 4., 2., 0.], [0., 0., 0., 0., 0.]])
- class skimage.feature.BRIEF(descriptor_size=256, patch_size=49, mode='normal', sigma=1, rng=1)[ソース]#
ベース:
DescriptorExtractorBRIEFバイナリ記述子抽出器。
BRIEF (Binary Robust Independent Elementary Features) は、効率的な特徴点記述子です。比較的少ないビット数を使用した場合でも非常に識別力が高く、単純な強度差テストを使用して計算されます。
各キーポイントについて、N 個のピクセルペアの特定の分布に対して強度比較が行われ、その結果、長さ N のバイナリ記述子が生成されます。バイナリ記述子の場合、ハミング距離を特徴マッチングに使用できます。これにより、L2 ノルムと比較して計算コストが低くなります。
- パラメータ:
- descriptor_sizeint, オプション
各キーポイントの BRIEF 記述子のサイズ。作者によって推奨されるサイズは 128、256、および 512 です。デフォルトは 256 です。
- patch_sizeint, オプション
キーポイント周辺の2次元正方形パッチサンプリング領域の長さ。デフォルトは 49 です。
- mode{‘normal’, ‘uniform’}, オプション
キーポイント周辺の決定ピクセルペアのサンプリング位置の確率分布。
- rng{
numpy.random.Generator, int}, optional 擬似乱数ジェネレーター (RNG)。デフォルトでは、PCG64 ジェネレーターが使用されます (
numpy.random.default_rng()を参照)。rngが int の場合、ジェネレーターのシードに使用されます。PRNG は、決定ピクセルペアのランダムサンプリングに使用されます。長さ
patch_sizeの正方形ウィンドウから、強度比較を使用して記述子を作成するために、modeパラメータを使用してピクセルペアがサンプリングされます。画像間でマッチングするには、同じ
rngを使用して記述子を作成する必要があります。これを容易にするためrngはデフォルトで 1 になります。extractメソッドのその後の呼び出しでは、同じ rng/シードが使用されます。
- sigmafloat, optional
ノイズ感度を軽減するために画像に適用されるガウスローパスフィルターの標準偏差。これは、識別力が高く優れた記述子を取得するために強く推奨されます。
- 属性:
- descriptors(Q,
descriptor_size) dtype bool の配列 インデックス
(i, j)での値がTrueまたはFalseのいずれかである境界キーポイントをフィルタリングした後、Q 個のキーポイントのサイズdescriptor_sizeのバイナリ記述子の 2D ndarray。これは、i 番目のキーポイントに対する j 番目の決定ピクセルペアの強度比較の結果を表します。これはQ == np.sum(mask)です。- mask(N,) dtype bool の配列
キーポイントがフィルタリングされたかどうか(
False)またはdescriptors配列に記述されているかどうか(True)を示すマスク。
- descriptors(Q,
例
>>> from skimage.feature import (corner_harris, corner_peaks, BRIEF, ... match_descriptors) >>> import numpy as np >>> square1 = np.zeros((8, 8), dtype=np.int32) >>> square1[2:6, 2:6] = 1 >>> square1 array([[0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0]], dtype=int32) >>> square2 = np.zeros((9, 9), dtype=np.int32) >>> square2[2:7, 2:7] = 1 >>> square2 array([[0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0]], dtype=int32) >>> keypoints1 = corner_peaks(corner_harris(square1), min_distance=1) >>> keypoints2 = corner_peaks(corner_harris(square2), min_distance=1) >>> extractor = BRIEF(patch_size=5) >>> extractor.extract(square1, keypoints1) >>> descriptors1 = extractor.descriptors >>> extractor.extract(square2, keypoints2) >>> descriptors2 = extractor.descriptors >>> matches = match_descriptors(descriptors1, descriptors2) >>> matches array([[0, 0], [1, 1], [2, 2], [3, 3]]) >>> keypoints1[matches[:, 0]] array([[2, 2], [2, 5], [5, 2], [5, 5]]) >>> keypoints2[matches[:, 1]] array([[2, 2], [2, 6], [6, 2], [6, 6]])
- class skimage.feature.CENSURE(min_scale=1, max_scale=7, mode='DoB', non_max_threshold=0.15, line_threshold=10)[ソース]#
基底クラス:
FeatureDetectorCENSUREキーポイント検出器。
- min_scaleint, optional
キーポイントを抽出する最小スケール。
- max_scaleint, optional
キーポイントを抽出する最大スケール。キーポイントは、最初のスケールと最後のスケールを除いた、[min_scale + 1, max_scale - 1]の範囲のすべてのスケールから抽出されます。異なるスケールのフィルターサイズは、隣接する2つのスケールがオクターブを構成するように設定されています。
- mode{‘DoB’, ‘Octagon’, ‘STAR’}, optional
入力画像のスケールを取得するために使用される二値フィルタの種類。指定可能な値は、'DoB'、'Octagon'、'STAR'です。3つのモードは、二値フィルタの形状(それぞれ、ボックス(正方形)、八角形、星形)を表します。たとえば、二値の八角形フィルタは、小さい内側の八角形と大きい外側の八角形で構成され、フィルタの重みは、内側の八角形の両方で一様に負で、差分領域では一様に正です。より優れた特徴のためにはSTARおよびOctagonを使用し、より優れたパフォーマンスのためにはDoBを使用します。
- non_max_thresholdfloat, optional
非最大抑制後に得られた、弱いマグニチュード応答を持つ極大値と極小値を抑制するために使用されるしきい値。
- line_thresholdfloat, optional
主曲率の比率がこの値よりも大きい興味点を拒否するためのしきい値。
- 属性:
- keypoints(N, 2) 配列
キーポイントの座標を
(行, 列)で表したもの。- scales(N,) 配列
対応するスケール。
参考文献
[1]Motilal Agrawal、Kurt Konolige、Morten Rufus Blas「CENSURE: Center Surround Extremas for Realtime Feature Detection and Matching」、https://link.springer.com/chapter/10.1007/978-3-540-88693-8_8 DOI:10.1007/978-3-540-88693-8_8
[2]Adam Schmidt、Marek Kraft、Michal Fularz、Zuzanna Domagala「ロボットナビゲーションのコンテキストにおけるポイント特徴検出器と記述子の比較評価」http://yadda.icm.edu.pl/yadda/element/bwmeta1.element.baztech-268aaf28-0faf-4872-a4df-7e2e61cb364c/c/Schmidt_comparative.pdf DOI:10.1.1.465.1117
例
>>> from skimage.data import astronaut >>> from skimage.color import rgb2gray >>> from skimage.feature import CENSURE >>> img = rgb2gray(astronaut()[100:300, 100:300]) >>> censure = CENSURE() >>> censure.detect(img) >>> censure.keypoints array([[ 4, 148], [ 12, 73], [ 21, 176], [ 91, 22], [ 93, 56], [ 94, 22], [ 95, 54], [100, 51], [103, 51], [106, 67], [108, 15], [117, 20], [122, 60], [125, 37], [129, 37], [133, 76], [145, 44], [146, 94], [150, 114], [153, 33], [154, 156], [155, 151], [184, 63]]) >>> censure.scales array([2, 6, 6, 2, 4, 3, 2, 3, 2, 6, 3, 2, 2, 3, 2, 2, 2, 3, 2, 2, 4, 2, 2])
- class skimage.feature.Cascade#
基底クラス:
objectオブジェクト検出に使用される分類器のカスケードのクラス。
カスケード分類器の背後にある主な考え方は、精度の高い分類器を1つだけ作成する代わりに、中程度の精度の分類器を作成し、それらを1つの強力な分類器にアンサンブルすることです。カスケード分類器の2番目の利点は、カスケード内の一部の分類器のみを評価することによって簡単な例を分類できるため、1つの強力な分類器を評価するプロセスよりもはるかに高速になることです。
- 属性:
- epscnp.float32_t
精度パラメータ。これを増やすと、分類器が検出する偽陽性が少なくなる一方で、偽陰性のスコアが増加します。
- stages_numberPy_ssize_t
カスケード内のステージ数。各カスケードは、トレーニングされた特徴であるスタンプで構成されています。
- stumps_numberPy_ssize_t
カスケードのすべてのステージにおけるスタンプの合計数。
- features_numberPy_ssize_t
カスケードで使用される異なる特徴の合計数。2つのスタンプは同じ特徴を使用できますが、トレーニングされた値は異なります。
- window_widthPy_ssize_t
使用される検出ウィンドウの幅。このウィンドウよりも小さいオブジェクトは検出できません。
- window_heightPy_ssize_t
検出ウィンドウの高さ。
- stagesStage*
Stage構造体を使用してステージ情報を格納するC配列へのポインタ。
- featuresMBLBP*
MBLBP構造体を使用してMBLBP特徴を格納するC配列へのポインタ。
- LUTscnp.uint32_t*
トレーニングされたMBLBP特徴(MBLBPStumps)が特定の領域を評価するために使用するルックアップテーブルを備えたC配列へのポインタ。
注釈
カスケードアプローチは、ViolaとJonesによって最初に記述されました[1]、[2]、ただし、これらの最初の出版物では、一連のHaarライクな特徴を使用していました。この実装では、代わりにマルチスケールブロックローカルバイナリパターン(MB-LBP)特徴を使用します[3]。
参考文献
[1]Viola, P. および Jones, M. 「単純な特徴のブーストカスケードを使用した高速オブジェクト検出」、In: 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognitionの議事録。CVPR 2001、pp. I-I。 DOI:10.1109/CVPR.2001.990517
[2]Viola, P. および Jones, M.J, 「ロバストなリアルタイム顔検出」、International Journal of Computer Vision 57、137–154(2004)。 DOI:10.1023/B:VISI.0000013087.49260.fb
[3]Liao, S. 他。 顔認識のためのマルチスケールブロックローカルバイナリパターンの学習。国際バイオメトリクス会議(ICB)、2007年、pp. 828-837。In: Lecture Notes in Computer Science、vol 4642。Springer、ベルリン、ハイデルベルク。 DOI:10.1007/978-3-540-74549-5_87
- __init__()#
カスケード分類器を初期化します。
- パラメータ:
- xml_fileファイルのパスまたはファイルのオブジェクト
すべてのカスケード分類器のパラメータがロードされるOpenCv形式のファイル。
- epscnp.float32_t
精度パラメータ。これを増やすと、分類器が検出する偽陽性が少なくなる一方で、偽陰性のスコアが増加します。
- detect_multi_scale(img, scale_factor, step_ratio, min_size, max_size, min_neighbor_number=4, intersection_score_threshold=0.5)#
入力画像の複数のスケールでオブジェクトを検索します。
この関数は、入力画像、各ステップで検索ウィンドウが乗算されるスケールファクター、最小ウィンドウサイズ、およびオブジェクトを検出するために入力画像に適用される検索ウィンドウの間隔を指定する最大ウィンドウサイズを取得します。
- パラメータ:
- img2-Dまたは3-D ndarray
入力画像を表すNdarray。
- scale_factorcnp.float32_t
各ステップで検索ウィンドウが乗算されるスケール。
- step_ratiocnp.float32_t
画像のスケーリングごとに検索ステップを乗算する比率。1は徹底的な検索を表し、通常は遅いです。このパラメータを高い値に設定すると、結果は悪化しますが、計算ははるかに速くなります。通常、[1, 1.5] の範囲の値が良い結果をもたらします。
- min_sizetuple (int, int)
検索ウィンドウの最小サイズ。
- max_sizetuple (int, int)
検索ウィンドウの最大サイズ。
- min_neighbor_numberint
検出が関数によって承認されるための、交差する検出の最小数。
- intersection_score_thresholdcnp.float32_t
2つの検出を1つにマージするための、(交差領域) / (小さい長方形の領域) の比率の最小値。
- 戻り値:
- outputlist of dicts
辞書は {‘r’: int, ‘c’: int, ‘width’: int, ‘height’: int} の形式を持ち、’r’ は検出されたウィンドウの左上隅の行位置、’c’ は列位置、’width’ は検出されたウィンドウの幅、’height’ は検出されたウィンドウの高さを表します。
- eps#
- features_number#
- stages_number#
- stumps_number#
- window_height#
- window_width#
- class skimage.feature.ORB(downscale=1.2, n_scales=8, n_keypoints=500, fast_n=9, fast_threshold=0.08, harris_k=0.04)[ソース]#
ベース:
FeatureDetector,DescriptorExtractor方向付けされたFASTおよび回転されたBRIEF特徴検出器とバイナリ記述子抽出器。
- パラメータ:
- n_keypointsint, optional
返されるキーポイントの数。検出されたキーポイントが
n_keypointsより多い場合、関数はハリスのコーナー応答に基づいて最適なn_keypointsを返します。そうでない場合は、検出されたすべてのキーポイントが返されます。- fast_nint, optional
skimage.feature.corner_fastのnパラメータ。円上の16ピクセルのうち、テストピクセルに対してすべて明るいまたは暗い連続したピクセルの最小数。円上の点 c は、Ic < Ip - thresholdの場合、テストピクセル p に対して暗く、Ic > Ip + thresholdの場合、明るくなります。また、FAST-nコーナー検出器の n を表します。- fast_thresholdfloat, optional
feature.corner_fastのthresholdパラメータ。円上のピクセルが、テストピクセルに対して明るい、暗い、または類似しているかを判断するために使用される閾値。より多くのコーナーが必要な場合は閾値を下げ、その逆も同様です。- harris_kfloat, optional
skimage.feature.corner_harrisのkパラメータ。通常[0, 0.2]の範囲で、エッジからコーナーを分離するための感度係数。kの値を小さくすると、鋭いコーナーが検出されます。- downscalefloat, optional
画像ピラミッドのダウン スケール係数。デフォルト値の 1.2 は、その後の特徴記述に対してロバストなスケール不変性を可能にする、より密なスケールが存在するように選択されています。
- n_scalesint, optional
画像ピラミッドの最下部から特徴を抽出する最大スケール数。
- 属性:
- keypoints(N, 2) 配列
キーポイントの座標を
(行, 列)で表したもの。- scales(N,) 配列
対応するスケール。
- orientations(N,) array
対応するラジアン単位の方位。
- responses(N,) array
対応するハリスのコーナー応答。
- descriptors(Q,
descriptor_size) dtype bool の配列 インデックス
(i, j)の値がTrueまたはFalseのいずれかである、境界キーポイントをフィルタリングした後の Q キーポイントのサイズdescriptor_sizeの2次元バイナリ記述子の配列。これは、i 番目のキーポイントに関する j 番目の決定ピクセルペアの強度比較の結果を表します。Q == np.sum(mask)です。
参考文献
[1]Ethan Rublee, Vincent Rabaud, Kurt Konolige and Gary Bradski “ORB: An efficient alternative to SIFT and SURF” http://www.vision.cs.chubu.ac.jp/CV-R/pdf/Rublee_iccv2011.pdf
例
>>> from skimage.feature import ORB, match_descriptors >>> img1 = np.zeros((100, 100)) >>> img2 = np.zeros_like(img1) >>> rng = np.random.default_rng(19481137) # do not copy this value >>> square = rng.random((20, 20)) >>> img1[40:60, 40:60] = square >>> img2[53:73, 53:73] = square >>> detector_extractor1 = ORB(n_keypoints=5) >>> detector_extractor2 = ORB(n_keypoints=5) >>> detector_extractor1.detect_and_extract(img1) >>> detector_extractor2.detect_and_extract(img2) >>> matches = match_descriptors(detector_extractor1.descriptors, ... detector_extractor2.descriptors) >>> matches array([[0, 0], [1, 1], [2, 2], [3, 4], [4, 3]]) >>> detector_extractor1.keypoints[matches[:, 0]] array([[59. , 59. ], [40. , 40. ], [57. , 40. ], [46. , 58. ], [58.8, 58.8]]) >>> detector_extractor2.keypoints[matches[:, 1]] array([[72., 72.], [53., 53.], [70., 53.], [59., 71.], [72., 72.]])
- __init__(downscale=1.2, n_scales=8, n_keypoints=500, fast_n=9, fast_threshold=0.08, harris_k=0.04)[ソース]#
- detect_and_extract(image)[ソース]#
向き付けされた FAST キーポイントを検出して、rBRIEF 記述子を抽出します。
これは、最初に
detectを呼び出し、次にextractを呼び出すよりも高速であることに注意してください。- パラメータ:
- image2D array
入力画像。
- extract(image, keypoints, scales, orientations)[ソース]#
画像内の指定されたキーポイントに対して、rBRIEF バイナリ記述子を抽出します。
キーポイントは、同じ
downscaleおよびn_scalesパラメータを使用して抽出する必要があることに注意してください。さらに、キーポイントと記述子の両方を抽出する場合は、より高速なdetect_and_extractを使用する必要があります。- パラメータ:
- image2D array
入力画像。
- keypoints(N, 2) 配列
キーポイントの座標を
(行, 列)で表したもの。- scales(N,) 配列
対応するスケール。
- orientations(N,) array
対応するラジアン単位の方位。
- class skimage.feature.SIFT(upsampling=2, n_octaves=8, n_scales=3, sigma_min=1.6, sigma_in=0.5, c_dog=0.013333333333333334, c_edge=10, n_bins=36, lambda_ori=1.5, c_max=0.8, lambda_descr=6, n_hist=4, n_ori=8)[source]#
ベース:
FeatureDetector,DescriptorExtractorSIFT特徴検出および記述子抽出。
- パラメータ:
- upsamplingint, optional
特徴検出の前に、画像は1(アップスケーリングなし)、2、または4の係数でアップスケールされます。方法:バイキュービック補間。
- n_octavesint, optional
オクターブの最大数。オクターブごとに、画像サイズは半分になり、シグマは2倍になります。最小スケールで各次元に沿って少なくとも12ピクセルを維持するために、オクターブ数は必要に応じて減らされます。
- n_scalesint, optional
各オクターブのスケールの最大数。
- sigma_minfloat, オプション
シード画像のぼかしレベル。アップサンプリングが有効になっている場合、sigma_minは係数1/upsamplingでスケーリングされます。
- sigma_infloat, optional
入力画像の想定されるぼかしレベル。
- c_dogfloat, optional
DoG内の低コントラスト極値を破棄するための閾値。最終的な値は、次の関係によってn_scalesに依存します:final_c_dog = (2^(1/n_scales)-1) / (2^(1/3)-1) * c_dog
- c_edgefloat, optional
エッジにある極値を破棄するための閾値。Hが極値のヘシアンである場合、その「エッジネス」はtr(H)²/det(H)で表されます。エッジネスが(c_edge + 1)²/c_edgeよりも大きい場合、極値は破棄されます。
- n_binsint, optional
キーポイント周辺の勾配方向を記述するヒストグラム内のビンの数。
- lambda_orifloat, optional
キーポイントの基準方向を見つけるために使用されるウィンドウの幅は6 * lambda_ori * sigmaであり、2 * lambda_ori * sigmaの標準偏差で重み付けされます。
- c_maxfloat, optional
方向ヒストグラムの二次ピークが方向として受け入れられる閾値。
- lambda_descrfloat, optional
キーポイントの記述子を定義するために使用されるウィンドウの幅は2 * lambda_descr * sigma * (n_hist+1)/n_histであり、lambda_descr * sigmaの標準偏差で重み付けされます。
- n_histint, optional
キーポイントの記述子を定義するために使用されるウィンドウは、n_hist * n_hist個のヒストグラムで構成されます。
- n_oriint, optional
記述子パッチのヒストグラム内のビンの数。
- 属性:
- delta_minfloat
最初のオクターブのサンプリング距離。最終的な値は1/upsamplingです。
- float_dtypetype
画像のデータ型。
- scalespace_sigmas(n_octaves, n_scales + 3) array
すべてのオクターブのすべてのスケールのシグマ値。
- keypoints(N, 2) 配列
キーポイントの座標を
(行, 列)で表したもの。- positions(N, 2) array
サブピクセル精度のキーポイント座標(
(row, col))。- sigmas(N,) array
キーポイントの対応するシグマ(ぼかし)値。
- scales(N,) 配列
キーポイントの対応するスケール。
- orientations(N,) array
すべてのキーポイント周辺の勾配の向き。
- octaves(N,) array
キーポイントの対応するオクターブ。
- descriptors(N, n_hist*n_hist*n_ori) array
キーポイントの記述子。
注釈
SIFTアルゴリズムはDavid Loweによって開発されました[1], [2]、後にブリティッシュコロンビア大学によって特許取得されました。2020年に特許が失効したため、自由に使用できます。ここでの実装は、[3]の詳細な説明に厳密に従っており、同じデフォルトパラメータの使用を含みます。
参考文献
[1]D.G. Lowe. “Object recognition from local scale-invariant features”, Proceedings of the Seventh IEEE International Conference on Computer Vision, 1999, vol.2, pp. 1150-1157. DOI:10.1109/ICCV.1999.790410
[2]D.G. Lowe. “Distinctive Image Features from Scale-Invariant Keypoints”, International Journal of Computer Vision, 2004, vol. 60, pp. 91–110. DOI:10.1023/B:VISI.0000029664.99615.94
[3]I. R. Otero and M. Delbracio. “Anatomy of the SIFT Method”, Image Processing On Line, 4 (2014), pp. 370–396. DOI:10.5201/ipol.2014.82
例
>>> from skimage.feature import SIFT, match_descriptors >>> from skimage.data import camera >>> from skimage.transform import rotate >>> img1 = camera() >>> img2 = rotate(camera(), 90) >>> detector_extractor1 = SIFT() >>> detector_extractor2 = SIFT() >>> detector_extractor1.detect_and_extract(img1) >>> detector_extractor2.detect_and_extract(img2) >>> matches = match_descriptors(detector_extractor1.descriptors, ... detector_extractor2.descriptors, ... max_ratio=0.6) >>> matches[10:15] array([[ 10, 412], [ 11, 417], [ 12, 407], [ 13, 411], [ 14, 406]]) >>> detector_extractor1.keypoints[matches[10:15, 0]] array([[ 95, 214], [ 97, 211], [ 97, 218], [102, 215], [104, 218]]) >>> detector_extractor2.keypoints[matches[10:15, 1]] array([[297, 95], [301, 97], [294, 97], [297, 102], [293, 104]])
- __init__(upsampling=2, n_octaves=8, n_scales=3, sigma_min=1.6, sigma_in=0.5, c_dog=0.013333333333333334, c_edge=10, n_bins=36, lambda_ori=1.5, c_max=0.8, lambda_descr=6, n_hist=4, n_ori=8)[source]#
- property deltas#
すべてのオクターブのサンプリング距離