pandas を使用した領域特性の探索と可視化

この簡単な例では、10枚の画像シリーズの各ラベル付き領域のサイズを計算する方法を示します。2D画像と3D画像を使用します。ブロブ状の領域は合成的に生成されます。体積分率（つまり、ブロブによって覆われたピクセルまたはボクセルの比率）が増加すると、ブロブ（領域）の数は減少し、単一領域のサイズ（面積または体積）は大きくなります。面積（サイズ）の値はpandasと互換性のある形式で利用できるため、便利なデータ分析と可視化が可能になります。

面積以外にも、多くの領域特性が利用可能です。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns

from skimage import data, measure


fractions = np.linspace(0.05, 0.5, 10)

2D画像

images = [data.binary_blobs(volume_fraction=f) for f in fractions]

labeled_images = [measure.label(image) for image in images]

properties = ['label', 'area']

tables = [
    measure.regionprops_table(image, properties=properties) for image in labeled_images
]
tables = [pd.DataFrame(table) for table in tables]

for fraction, table in zip(fractions, tables):
    table['volume fraction'] = fraction

areas = pd.concat(tables, axis=0)

# Create custom grid of subplots
grid = plt.GridSpec(2, 2)
ax1 = plt.subplot(grid[0, 0])
ax2 = plt.subplot(grid[0, 1])
ax = plt.subplot(grid[1, :])
# Show image with lowest volume fraction
ax1.imshow(images[0], cmap='gray_r')
ax1.set_axis_off()
ax1.set_title(f'fraction {fractions[0]}')
# Show image with highest volume fraction
ax2.imshow(images[-1], cmap='gray_r')
ax2.set_axis_off()
ax2.set_title(f'fraction {fractions[-1]}')
# Plot area vs volume fraction
areas.plot(x='volume fraction', y='area', kind='scatter', ax=ax)
plt.show()

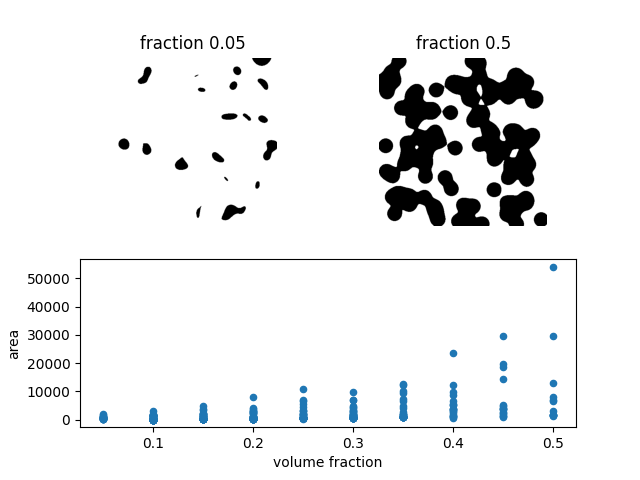
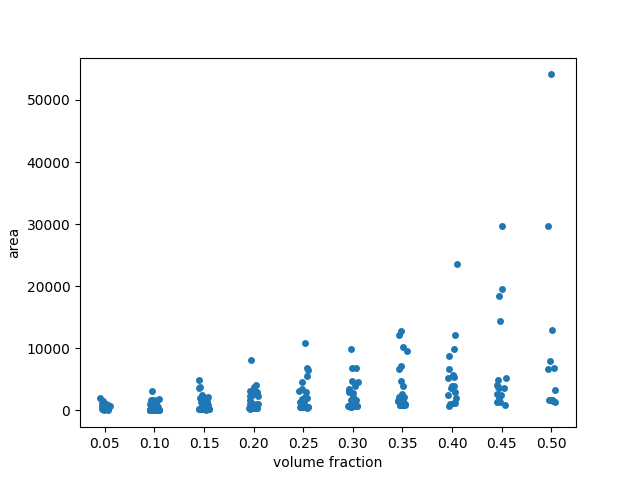
散布図では、多くの点が小さな面積値で重なっているように見えます。分布をよりよく理解するために、可視化にいくつかの「ジッター」を追加したい場合があります。この目的のために、引数jitter=Trueを使用してseaborn.stripplot（統計データ可視化のためのseabornライブラリから）を使用します。

fig, ax = plt.subplots()
sns.stripplot(x='volume fraction', y='area', data=areas, jitter=True, ax=ax)
# Fix floating point rendering
ax.set_xticklabels([f'{frac:.2f}' for frac in fractions])
plt.show()

/home/runner/work/scikit-image/scikit-image/doc/examples/segmentation/plot_regionprops_table.py:75: UserWarning:

set_ticklabels() should only be used with a fixed number of ticks, i.e. after set_ticks() or using a FixedLocator.

3D画像

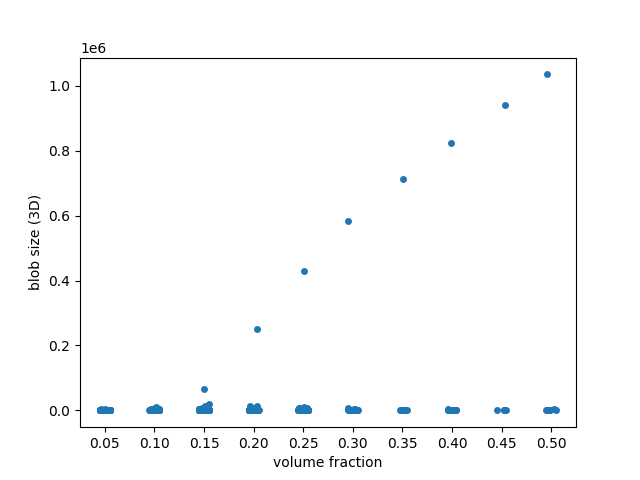
3Dで同じ分析を行うと、はるかに劇的な挙動が見られます。体積分率が約0.25を超えると、ブロブは単一の巨大な塊に合体します。これは、統計物理学とグラフ理論におけるパーコレーション閾値に対応します。

images = [data.binary_blobs(length=128, n_dim=3, volume_fraction=f) for f in fractions]

labeled_images = [measure.label(image) for image in images]

properties = ['label', 'area']

tables = [
    measure.regionprops_table(image, properties=properties) for image in labeled_images
]
tables = [pd.DataFrame(table) for table in tables]

for fraction, table in zip(fractions, tables):
    table['volume fraction'] = fraction

blob_volumes = pd.concat(tables, axis=0)

fig, ax = plt.subplots()
sns.stripplot(x='volume fraction', y='area', data=blob_volumes, jitter=True, ax=ax)
ax.set_ylabel('blob size (3D)')
# Fix floating point rendering
ax.set_xticklabels([f'{frac:.2f}' for frac in fractions])
plt.show()

/home/runner/work/scikit-image/scikit-image/doc/examples/segmentation/plot_regionprops_table.py:107: UserWarning:

set_ticklabels() should only be used with a fixed number of ticks, i.e. after set_ticks() or using a FixedLocator.